Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-10T11:00:38.321Z Has data issue: false hasContentIssue false
  • English
  • Français

On the involution fixity of simple groups

Part of: Representation theory of groups Permutation groups

Published online by Cambridge University Press:  04 June 2021

Timothy C. Burness  and
Elisa Covato
Timothy C. Burness
Affiliation:
School of Mathematics, University of Bristol, BristolBS8 1UG, UK (t.burness@bristol.ac.uk)
Elisa Covato
Affiliation:
Bristol, UK (elisa.covato@gmail.com)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 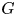$G$ be a finite permutation group of degree 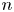$n$ and let 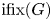${\rm ifix}(G)$ be the involution fixity of 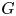$G$, which is the maximum number of fixed points of an involution. In this paper, we study the involution fixity of almost simple primitive groups whose socle $T$ is an alternating or sporadic group; our main result classifies the groups of this form with 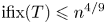${\rm ifix}(T) \leqslant n^{4/9}$. This builds on earlier work of Burness and Thomas, who studied the case where 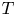$T$ is an exceptional group of Lie type, and it strengthens the bound 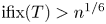${\rm ifix}(T) > n^{1/6}$ (with prescribed exceptions), which was proved by Liebeck and Shalev in 2015. A similar result for classical groups will be established in a sequel.

Keywords

Primitive groupssimple groupsinvolution fixity

MSC classification

Primary: 20B15: Primitive groups 20D06: Simple groups
Secondary: 20B35: Subgroups of symmetric groups 20D08: Simple groups
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 64 , Issue 2 , May 2021 , pp. 408 - 426
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bamberg, J., Popiel, T. and Praeger, C. E., Simple groups, product actions, and generalized quadrangles, Nagoya Math. J. 234 (2019), 87–126.CrossRefGoogle Scholar
Bender, H., Transitive Gruppen gerader Ordnung, in denen jede Involution genau einen Punkt festlässt, J. Algebra 17 (1971), 527–554.CrossRefGoogle Scholar
Bosma, W., Cannon, J. and Playoust, C., The Magma algebra system I: the user language, J. Symb. Comput. 24 (1997), 235–265.10.1006/jsco.1996.0125CrossRefGoogle Scholar
Breuer, T., The GAP Character Table Library, Version 1.2.1, GAP package, available at http://www.math.rwth-aachen.de/~Thomas.Breuer/ctbllib, 2012Google Scholar
Burness, T. C., Simple groups, fixed point ratios and applications, in Local representation theory and simple groups, pp. 267–322, EMS Ser. Lect. Math. (Eur. Math. Soc., Zürich, 2018).10.4171/185-1/6CrossRefGoogle Scholar
Burness, T. C. and Giudici, M., Classical groups, derangements and primes, Australian Mathematical Society Lecture Series, Volume 25 (Cambridge University Press, Cambridge, 2016).CrossRefGoogle Scholar
Burness, T. C., O'Brien, E. A. and Wilson, R. A., Base sizes for sporadic simple groups, Israel J. Math. 177 (2010), 307–333.CrossRefGoogle Scholar
Burness, T. C. and Thomas, A. R., On the involution fixity of exceptional groups of Lie type, Internat. J. Algebra Comput. 28 (2018), 411–466.CrossRefGoogle Scholar
Conway, J. H., Curtis, R. T., Norton, S. P., Parker, R. A. and Wilson, R. A., Atlas of finite groups (Oxford University Press, 1985).Google Scholar
The GAP Group, GAP – Groups, Algorithms, and Programming, Version 4.11.0, available at http://www.gap-system.org, 2020.Google Scholar
Guest, S., Morris, J., Praeger, C. E. and Spiga, P., On the maximum orders of elements of finite almost simple groups and primitive permutation groups, Trans. Amer. Math. Soc. 367 (2015), 7665–7694.10.1090/S0002-9947-2015-06293-XCrossRefGoogle Scholar
Isaacs, I. M., Character theory of finite groups, Pure and Applied Mathematics, Volume 69 (Academic Press, New York-London, 1976).Google Scholar
Kleidman, P. B. and Liebeck, M. W., The subgroup structure of the finite classical groups, London Math. Soc. Lecture Note Series, Volume 129 (Cambridge University Press, 1990).CrossRefGoogle Scholar
Liebeck, M. W., Praeger, C. E. and Saxl, J., A classification of the maximal subgroups of the finite alternating and symmetric groups, J. Algebra 111 (1987), 365–383.CrossRefGoogle Scholar
Liebeck, M. W. and Saxl, J., On point stabilizers in primitive permutation groups, Comm. Algebra 19 (1991), 2777–2786.CrossRefGoogle Scholar
Liebeck, M. W. and Saxl, J., Maximal subgroups of finite simple groups and their automorphism groups, in Proceedings of the International Conference on Algebra, Part 1 (Novosibirsk, 1989), Contemp. Math., Volume 131, pp. 243–259 (American Mathematical Society, Providence, RI, 1992).CrossRefGoogle Scholar
Liebeck, M. W. and Shalev, A., On fixed points of elements in primitive permutation groups, J. Algebra 421 (2015), 438–459.CrossRefGoogle Scholar
Magaard, K. and Waldecker, R., Transitive permutation groups where nontrivial elements have at most two fixed points, J. Pure Appl. Algebra 219 (2015), 729–759.10.1016/j.jpaa.2014.04.027CrossRefGoogle Scholar
Pribitkin, W., Simple upper bounds for partition functions, Ramanujan J. 18 (2009), 113–119.CrossRefGoogle Scholar
Quick, M., Probabilistic generation of wreath products of non-abelian finite simple groups, Comm. Algebra 32 (2004), 4753–4768.CrossRefGoogle Scholar
Ronse, C., On permutation groups of prime power order, Math. Z. 173 (1980), 211–215.CrossRefGoogle Scholar
Saxl, J. and Shalev, A., The fixity of permutation groups, J. Algebra 174 (1995), 1122–1140.CrossRefGoogle Scholar
Wilson, R. A., Maximal subgroups of sporadic groups, in Finite simple groups: thirty years of the Atlas and beyond, Contemp. Math., Volume 694, pp. 57–72 (American Mathematical Society, Providence, RI, 2017).CrossRefGoogle Scholar
Wilson, R. A., et al. , A World-Wide-Web Atlas of finite group representations, http://brauer.maths.qmul.ac.uk/Atlas/v3/Google Scholar