Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-02-04T01:59:24.950Z Has data issue: false hasContentIssue false
  • English
  • Français

On the structure of non-negative integer sets which have identical representation functions

Part of: Sequences and sets

Published online by Cambridge University Press:  03 February 2025

Cui-Fang Sun Open the ORCID record for Cui-Fang Sun [Opens in a new window]  and
Hao Pan
Cui-Fang Sun*
Affiliation:
School of Mathematics and Statistics, Anhui Normal University, Wuhu, Anhui, 241002, P.R. China
Hao Pan
Affiliation:
School of Mathematics and Statistics, Anhui Normal University, Wuhu, Anhui, 241002, P.R. China Department of Basic Courses, Lu’an Vocational Technical College, Lu’an, Anhui, 237001, P.R. China
*
Corresponding author: Cui-Fang Sun, email: cuifangsun@163.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Let $\mathbb{N}$ be the set of all non-negative integers. For any integer r and m, let 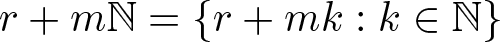$r+m\mathbb{N}=\{r+mk: k\in\mathbb{N}\}$. For $S\subseteq \mathbb{N}$ and 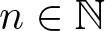$n\in \mathbb{N}$, let 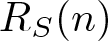$R_{S}(n)$ denote the number of solutions of the equation 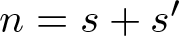$n=s+s'$ with 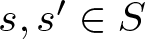$s, s'\in S$ and 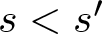$s \lt s'$. Let 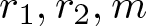$r_{1}, r_{2}, m$ be integers with $0 \lt r_{1} \lt r_{2} \lt m$ and $2\mid r_{1}$. In this paper, we prove that there exist two sets C and D with $C\cup D=\mathbb{N}$ and $C\cap D=(r_{1}+m\mathbb{N})\cup (r_{2}+m\mathbb{N})$ such that 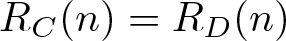$R_{C}(n)=R_{D}(n)$ for all 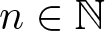$n\in\mathbb{N}$ if and only if there exists a positive integer l such that 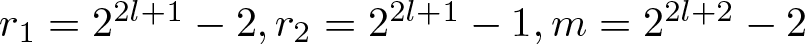$r_{1}=2^{2l+1}-2, r_{2}=2^{2l+1}-1, m=2^{2l+2}-2$.

Keywords

Sárközy’s problemrepresentation functionThue–Morse sequence

MSC classification

Primary: 11B34: Representation functions 11B83: Special sequences and polynomials
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , First View , pp. 1 - 20
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Chen, S. Q. and Chen, Y. G., Integer sets with identical representation functions II, European J. Combin. 94 (2021), .CrossRefGoogle Scholar
Chen, S. Q., Tang, M. and Yang, Q. H., On a problem of Chen and Lev, Bull. Aust. Math. Soc. 99 (2019), 15–22.CrossRefGoogle Scholar
Chen, Y. G. and Lev, V. F., Integer sets with identical representation functions, Integers 16 (2016), .Google Scholar
Chen, Y. G. and Tang, M., Partitions of natural numbers with the same representation functions, J. Number Theory 129 (2009), 2689–2695.CrossRefGoogle Scholar
Chen, Y. G. and Wang, B., On additive properties of two special sequences, Acta Arith. 110 (2003), 299–303.CrossRefGoogle Scholar
Dombi, G., Additive properties of certain sets, Acta Arith. 103 (2002), 137–146.CrossRefGoogle Scholar
Jiao, K. J., Sándor, C., Yang, Q. H. and Zhou, J. Y., On integer sets with the same representation functions, Bull. Aust. Math. Soc. 106 (2022), 224–235.CrossRefGoogle Scholar
Kiss, S. Z. and Sándor, C., Partitions of the set of nonnegative integers with the same representation functions, Discrete Math. 340 (2017), 1154–1161.CrossRefGoogle Scholar
Kiss, S. Z. and Sándor, C., On the structure of sets which have coinciding representation functions, Integers 19 (2019), .Google Scholar
Lev, V. F., Reconstructing integer sets from their representation functions, Electron. J. Combin. 11 (2004), .CrossRefGoogle Scholar
Li, J. W. and Tang, M., Partitions of the set of nonnegative integers with the same representation functions, Bull. Aust. Math. Soc. 97 (2018), 200–206.CrossRefGoogle Scholar
Sándor, C., Partitions of natural numbers and their representation functions, Integers 4 (2004), .Google Scholar
Sun, C. F. and Pan, H., Partitions of finite nonnegative integer sets with identical representation functions, Bull. Iranian Math. Soc. 49 (2023), .CrossRefGoogle Scholar
Sun, C. F., On finite nonnegative integer sets with identical representation functions, Ramanujan J. 65 (2024), 429–445.CrossRefGoogle Scholar
Tang, M. and Chen, S. Q., On a problem of partitions of the set of nonnegative integers with the same representation functions, Discrete Math. 341 (2018), 3075–3078.CrossRefGoogle Scholar
Tang, M. and Li, J. W., On the structure of some sets which have the same representation functions, Period. Math. Hungar. 77 (2018), 232–236.CrossRefGoogle Scholar
Tang, M., Partitions of the set of natural numbers and their representation functions, Discrete Math. 308 (2008), 2614–2616.CrossRefGoogle Scholar
Tang, M., Partitions of natural numbers and their representation functions, Chinese Ann. Math. Ser. A 37 (2016), 41–46, For English version, see Chinese J. Contemp. Math. 37 (2016), 39–44.Google Scholar
Yang, Q. H. and Chen, Y. G., Partitions of natural numbers with the same representation functions, J. Number Theory 132 (2012), 3047–3055.CrossRefGoogle Scholar
Yu, W. and Tang, M., A note on partitions of natural numbers and their representation functions, Integers 12 (2012), .Google Scholar