Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-11T04:14:53.743Z Has data issue: false hasContentIssue false
  • English
  • Français

Quasilinear Scalar Field Equations Involving Critical Sobolev Exponents and Potentials Vanishing at Infinity

Part of: Equations of mathematical physics and other areas of application Elliptic equations and systems Partial differential equations

Published online by Cambridge University Press:  30 April 2018

Athanasios N. Lyberopoulos
Athanasios N. Lyberopoulos*
Affiliation:
Department of Mathematics, University of the Aegean, 83200 Karlovassi, Samos, Greece (alyber@aegean.gr)
Get access Rights & Permissions [Opens in a new window]

Abstract

We are concerned with the existence of positive weak solutions, as well as the existence of bound states (i.e. solutions in W1, p (ℝN)), for quasilinear scalar field equations of the form

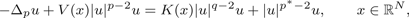$$ - \Delta _pu + V(x) \vert u \vert ^{p - 2}u = K(x) \vert u \vert ^{q - 2}u + \vert u \vert ^{p^ * - 2}u,\qquad x \in {\open R}^N,$$
where Δpu: = div(|∇ u|p−2∇u), 1 < p < N, p*: = Np/(N − p) is the critical Sobolev exponent, q ∈ (p, p*), while V(·) and K(·) are non-negative continuous potentials that may decay to zero as |x| → ∞ but are free from any integrability or symmetry assumptions.

Keywords

p-Laplaciannonlinear Schrödinger equationcritical Sobolev exponentsdecaying potentialspenalization methodlocal Palais–Smale condition

MSC classification

Primary: 35J92: Quasilinear elliptic equations with $p$-Laplacian
Secondary: 35Q55: NLS-like equations (nonlinear Schrödinger) 35Q74: PDEs in connection with mechanics of deformable solids 35B33: Critical exponents 35J20: Variational methods for second-order elliptic equations
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 61 , Issue 3 , August 2018 , pp. 705 - 733
Copyright
Copyright © Edinburgh Mathematical Society 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Alves, C. O., Existence of positive solutions for a problem with lack of compactness involving the p-Laplacian, Nonlinear Anal. 51 (2002), 1187–1206.Google Scholar
2Alves, C. O., do Ó, J. M. and Souto, M. A. S., Local mountain-pass for a class of elliptic problems in ℝN involving critical growth, Nonlinear Anal. 46 (2001), 495–510.Google Scholar
3Alves, C. O. and Souto, M. A. S., On existence and concentration behavior of ground state solutions for a class of problems with critical growth, Commun. Pure Appl. Anal. 1 (2002), 417–431.Google Scholar
4Alves, C. O. and Souto, M. A. S., Existence of solutions for a class of elliptic equations in ℝN with vanishing potentials, J. Differential Equations 252 (2012), 5555–5568.Google Scholar
5Ambrosetti, A., Badiale, M. and Cingolani, S., Semiclassical states of nonlinear Schrödinger equations, Arch. Rational Mech. Anal. 140 (1997), 285–300.CrossRefGoogle Scholar
6Ambrosetti, A., Felli, V. and Malchiodi, A., Ground states of nonlinear Schrödinger equations with potentials vanishing at infinity, J. Eur. Math. Soc. 7 (2005), 117–144.CrossRefGoogle Scholar
7Ambrosetti, A. and Malchiodi, A., Perturbation methods and semilinear elliptic problems on ℝN, Progress in Mathematics, Volume 240 (Birkhäuser, Basel, 2006)Google Scholar
8Ambrosetti, A., Malchiodi, A. and Ruiz, D., Bound states of nonlinear Schrödinger equations with potentials vanishing at infinity, J. Anal. Math. 98 (2006), 317–348.Google Scholar
9Ambrosetti, A. and Rabinowitz, P., Dual variational methods in critical point theory and applications, J. Funct. Anal. 14 (1973), 349–381.Google Scholar
10Astarita, G. and Marrucci, G., Principles of non-Newtonian fluid mechanics (McGraw-Hill, 1974).Google Scholar
11Aubin, T., Problèmes isopé rimétriques et espaces de Sobolev, J. Differential Geom. 11 (1976), 573–598.Google Scholar
12Benci, V., D'Avenia, P., Fortunato, D. and Pisani, L., Solitons in several space dimensions: Derrick's problem and infinitely many solutions, Arch. Rational Mech. Anal. 154 (2000), 297–324.Google Scholar
13Benci, V. and Cerami, G., Existence of positive solutions of the equation −Δu + a(x)u = u (N+2)/(N−2) in ℝN, J. Funct. Anal. 88 (1990), 90–117.CrossRefGoogle Scholar
14Benci, V., Grisanti, C. and Micheletti, A., Existence and non-existence of the ground state solution for the nonlinear Schrödinger equations with V(∞) = 0, Topol. Methods Nonlinear Anal. 26 (2005), 203–219.Google Scholar
15Berestycki, H. and Lions, P.-L., Nonlinear scalar field equations I, II, Arch. Rational Mech. Anal. 82 (1983), 313–345, 347–375.Google Scholar
16Berezin, F. A. and Shubin, M. A., The Schrödinger equation (Kluwer, Dordrecht, 1991).Google Scholar
17Bhattacharya, T., DiBenedetto, E. and Manfredi, J., Limits as p → ∞ of Δpup = f and related extremal problems, Rend. Sem. Mat. Univ. Politec. Torino Special Issue 47 (1989), 15–68.Google Scholar
18Bonheure, D. and Van Schaftingen, J., Ground states for the nonlinear Schrödinger equation with potential vanishing at infinity, Ann. Mat. Pura Appl. 189 (2010), 273–301.Google Scholar
19Brézis, H. and Nirenberg, L., Positive solutions of nonlinear elliptic equations involving critical Sobolev exponents, Commun. Pure Appl. Math. 36 (1983), 437–477.Google Scholar
20Cerami, G., Passaseo, D. and Solimini, S., Infinitely many positive solutions to some scalar field equations with nonsymmetric coefficients, Comm. Pure Appl. Math. 66 (2013), 372—413.CrossRefGoogle Scholar
21Chen, W., Wei, J. and Yan, S., Infinitely many solutions for the Schrödinger equations in ℝN with critical growth, J. Differential Equations 252 (2012), 2425–2447.CrossRefGoogle Scholar
22Damascelli, L., Merchan, S., Montoro, L. and Sciunzi, B., Radial symmetry and applications for a problem involving the −Δp(·) operator and critical nonlinearity in ℝN, Adv. Math. 265 (2014), 313–335.Google Scholar
23del Pino, M. and Felmer, P. L., Local mountain passes for semilinear elliptic problems in unbounded domains, Calc. Var. Partial Differential Equations 4 (1996), 121–137.CrossRefGoogle Scholar
24del Pino, M. and Felmer, P. L., Semi-classical states for nonlinear Schrödinger equations, J. Funct. Anal. 149 (1997), 245–265.Google Scholar
25del Pino, M. and Felmer, P. L., Semi-classical states of nonlinear Schrödinger equations: A variational reduction method, Math. Ann. 324 (2002), 1–32.CrossRefGoogle Scholar
26Derrick, G. H., Comments on nonlinear wave equations as models for elementary particles, J. Math. Phys. 5 (1964), 1252–1254.Google Scholar
27Díaz, J. I., Nonlinear partial differential equations and free boundaries, Vol. 1, Elliptic Equations, Pitman Research Notes in Mathematics, Volume 106 (Pitman, Boston, MA, 1985).Google Scholar
28Ding, W.-Y. and Ni, W.-M., On the existence of positive entire solutions of a semilinear elliptic equation, Arch. Rational Mech. Anal. 91 (1986), 283–308.Google Scholar
29Ding, Y. and Lin, F., Solutions of perturbed Schrödinger equations with critical nonlinearity, Calc. Var. Partial Differential Equations 30 (2007), 231–249.Google Scholar
30Ding, Y. and Wei, J., Semiclassical states for nonlinear Schrödinger equations with sign-changing potentials, J. Funct. Anal. 251 (2007), 546–572.Google Scholar
31do Ó, J. M., On existence and concentration of positive bound states of p-Laplacian equations in ℝN involving critical growth, Nonlinear Anal. 62 (2005), 777–801.CrossRefGoogle Scholar
32Figueiredo, G. M. and Furtado, M. F., Positive solutions for a quasilinear Schrödinger equation with critical growth, J. Dynam. Differential Equations 24 (2012), 13–28.Google Scholar
33Findley, W. N., Lai, J. S. and Onaran, K., Creep and relaxation of nonlinear viscoelastic materials – with an introduction to linear viscoelasticity, Series in Applied Mathematics and Mechanics, Volume 18 (North-Holland, Amsterdam–New York–Oxford, 1976).Google Scholar
34Floer, A. and Weinstein, A., Nonspreading wave packets for the cubic Schrödinger equation with a bounded potential, J. Funct. Anal. 69 (1986), 397–408.Google Scholar
35Guedda, M. and Veron, L., Quasilinear elliptic equations involving critical Sobolev exponents, Nonlinear Anal. 12 (1989), 879–902.Google Scholar
36He, C. and Li, G., The regularity of weak solutions to nonlinear scalar field elliptic equations containing p & q-Laplacians, Ann. Acad. Sci. Fenn. Math. 33 (2008), 337—371.Google Scholar
37Kabeya, Y., On some quasilinear elliptic problems involving critical Sobolev exponents, Funkcial. Ekvac. 36 (1993), 385–404.Google Scholar
38Kawohl, B., On a family of torsional creep problems, J. Reine Angew. Math. 410 (1990), 1–22.Google Scholar
39Lions, P.-L., The concentration-compactness principle in the calculus of variations. The limit case. Part I, Rev. Mat. Iberoamericana 1 (1985), 145–201.CrossRefGoogle Scholar
40Lyberopoulos, A. N., Quasilinear scalar field equations with competing potentials, J. Differential Equations 251 (2011), 3625–3657.Google Scholar
41Lyberopoulos, A. N., Bound states for a class of quasilinear scalar field equations with potentials vanishing at infinity, Acta Math. Sci. 32 (2012), 197–208.CrossRefGoogle Scholar
42Martinson, L. K. and Pavlov, K. B., The effect of magnetic plasticity in non-Newtonian fluids, Magnit. Gidrodinamika 3 (1969), 69–75.Google Scholar
43Martinson, L. K. and Pavlov, K. B., Unsteady shear flows of a conducting fluid with a rheological power flow, Magnit. Gidrodinamika 3 (1970), 5869–5875.Google Scholar
44Mercuri, C. and Squassina, M., Global compactness for a class of quasi-linear elliptic problems, Manuscripta Math. 140 (2013), 119–144.Google Scholar
45Mercuri, C. and Willem, M., A global compactness result for the p-Laplacian involving critical nonlinearities, Discrete Contin. Dyn. Syst. 28 (2010), 469–493.CrossRefGoogle Scholar
46Miyagaki, O. H., On a class of semilinear elliptic problems in ℝN with critical growth, Nonlinear Anal. 29 (1997), 773–781.Google Scholar
47Moroz, V. and Van Schaftingen, J., Semiclassical stationary states for nonlinear Schrödinger equations with fast decaying potentials, Calc. Var. Partial Differential Equations 37 (2010), 1–27.CrossRefGoogle Scholar
48Oh, Y.-G., Existence of semiclassical bound states of nonlinear Schrödinger equations with potential in the class (V)α, Comm. Partial Differential Equations 13 (1988), 1499–1519.Google Scholar
49Oh, Y.-G., Correction to ‘Existence of semiclassical bound states of nonlinear Schrödinger equations with potential in the class (V)α’, Comm. Partial Differential Equations 14 (1989), 833–834.Google Scholar
50Oh, Y.-G., On positive muti-lump bound states of nonlinear Schrödinger equations under multiple well potentials, Comm. Math. Phys. 131 (1990), 223–253.Google Scholar
51Pucci, P. and Serrin, J., The strong maximum principle revisited, J. Differential Equations 196 (2004), 1–66.Google Scholar
52Rabinowitz, P. H., On a class of nonlinear Schrödinger equations, Z. Angew. Math. Phys. 43 (1992), 270–291.CrossRefGoogle Scholar
53Sciunzi, B., Classification of positive D 1,p(ℝN)-solutions to the critical p-Laplace equation in ℝN, Adv. Math. 291 (2016), 12–23.Google Scholar
54Serrin, J. and Zou, H., Cauchy–Liouville and universal boundedness theorems for quasilinear elliptic equations and inequalities, Acta Math. 189 (2002), 79–142.Google Scholar
55Struwe, M., A global compactness result for elliptic boundary value problems involving limiting nonlinearities, Math. Z. 187 (1984), 511–517.CrossRefGoogle Scholar
56Sulem, C. and Sulem, P.-L., The nonlinear Schrödinger equation: self-focusing and wave collapse, Applied Mathematical Sciences, Volume 139 (Springer-Verlag, New York, 1999).Google Scholar
57Talenti, G., Best constant in Sobolev inequality, Ann. Mat. Pura Appl. 110 (1976), 353–372.Google Scholar
58Tolksdorf, P., Regularity for a more general class of quasilinear elliptic equations, J. Differential Equations 51 (1984), 126–150.Google Scholar
59Trudinger, N. S., On Harnack type inequalities and their application to quasilinear elliptic equations, Comm. Pure Appl. Math. 20 (1967), 721–747.Google Scholar
60Vétois, J., A priori estimates and application to the symmetry of solutions for critical p-Laplace equations, J. Differential Equations 260 (2016), 149–161.Google Scholar
61Wei, J. and Yan, S., New solutions for nonlinear Schrödinger equations with critical nonlinearity, J. Differential Equations 237 (2007), 446–472.Google Scholar
62Yang, J.-F. and Zhu, X.-P., On the existence of nontrivial solution of a quasilinear elliptic boundary value problem for unbounded domains. I. Positive mass case, Acta Math. Sci. 7 (1987), 341–359.Google Scholar
63Yang, J.-F. and Zhu, X.-P., The quasilinear elliptic equation on unbounded domain involving critical Sobolev exponent, J. Partial Differential Equations 2 (1989), 53–64.Google Scholar
64Yin, H. and Zhang, P., Bound states of nonlinear Schrödinger equations with potentials tending to zero at infinity, J. Differential Equations 247 (2009), 618–647.CrossRefGoogle Scholar
65Zou, H., Existence and non-existence for Schrödinger equations involving critical Sobolev exponents, J. Korean Math. Soc. 47 (2010), 547–572.CrossRefGoogle Scholar