Hostname: page-component-686fd747b7-8s9h2 Total loading time: 0 Render date: 2025-02-13T14:24:56.810Z Has data issue: false hasContentIssue false
  • English
  • Français

RETRACTED – The wigner property for CL-spaces and finite-dimensional polyhedral banach spaces

Part of: Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  04 June 2021

Dongni Tan  and
Xujian Huang
Dongni Tan
Affiliation:
School of Computer Science and Engineering, Tianjin University of Technology, Tianjin300384, P.R. China (tandongni0608@sina.cn)
Xujian Huang
Affiliation:
Department of Mathematics, Tianjin University of Technology, Tianjin300384, P.R. China (huangxujian86@sina.cn)
Get access Rights & Permissions [Opens in a new window]

Abstract

We say that a map $f$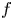 from a Banach space $X$ 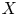to another Banach space $Y$ 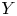is a phase-isometry if the equality

\[ \{\|f(x)+f(y)\|, \|f(x)-f(y)\|\}=\{\|x+y\|, \|x-y\|\} \]
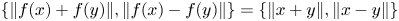
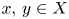holds for all $x,\,y\in X$. A Banach space $X$ 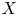is said to have the Wigner property if for any Banach space $Y$ 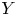and every surjective phase-isometry $f : X\rightarrow Y$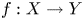, there exists a phase function $\varepsilon : X \rightarrow \{-1,\,1\}$ 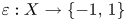such that $\varepsilon \cdot f$ 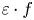is a linear isometry. We present some basic properties of phase-isometries between two real Banach spaces. These enable us to show that all finite-dimensional polyhedral Banach spaces and CL-spaces possess the Wigner property.

Keywords

the Wigner propertyphase-isometryCL-spacepolyhedral space

MSC classification

Primary: 46B20: Geometry and structure of normed linear spaces
Secondary: 46B04: Isometric theory of Banach spaces
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 64 , Issue 3 , August 2021 , pp. 717 - 733
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Cheng, L. X. and Li, M., Extreme points exposed points differentiability points in CL-spaces, Proc. Amer. Math. Soc. 136(7) (2008), 2445–2451.CrossRefGoogle Scholar
Chevalier, G., Wigner's theorem and its generalizations, in Handbook of quantum logic and quantum structures, pp. 429–475 (Elsevier Sci. B. V., Amsterdam, 2007).CrossRefGoogle Scholar
Fullerton, R. E., Geometrical characterization of certain function spaces, in Proc. Inter. Sympos. Linear Spaces, pp. 227–236, 1960 (Jerusalem Academic Press/Pergamon, Jerusalem/Oxford, 1961).Google Scholar
Gehér, Gy. P., An elementary proof for the non-bijective version of Wigner's theorem, Phys. Lett. A 378 (2014), 2054–2057.10.1016/j.physleta.2014.05.039CrossRefGoogle Scholar
Györy, M., A new proof of Wigner's theorem, Rep. Math. Phys. 54 (2004), 159–167.CrossRefGoogle Scholar
Hansen, A. B. and Lima, Å., The structure of finite dimensional Banach spaces with the 3.2 intersection property, Acta Math. 146 (1981), 1–23.CrossRefGoogle Scholar
Holmes, R. B., Geometric Functional Analysis and its Applications (New York, NY, Springer-Verlag, 1975).10.1007/978-1-4684-9369-6CrossRefGoogle Scholar
Huang, X. and Tan, D., Wigner's theorem in atomic $L_p$-spaces $(p>0)$, Publ. Math. Debrecen 92(34) (2018), 411–418.0)$' href=https://dx.doi.org/10.5486/PMD.2018.8005>CrossRef0)$' href=https://scholar.google.com/scholar_lookup?title=Wigner's+theorem+in+atomic+%24L_p%24-spaces+%24(p%3E0)%24&author=Huang+X.&author=Tan+D.&publication+year=2018&journal=Publ.+Math.+Debrecen&volume=92&doi=10.5486%2FPMD.2018.8005&pages=411-418>Google Scholar
Jia, W. and Tan, D., Wigner's theorem in $\mathcal {L}^{\infty }(\Gamma )$-type spaces, Bull. Austral. Math. Soc. 97(2) (2018), 279–284.CrossRefGoogle Scholar
Lima, Å., Intersection properties of balls and subspaces in Banach spaces, Trans. Amer. Math. Soc. 227 (1977), 1–62.CrossRefGoogle Scholar
López, G., Martín, M. and Payá, R., Real Banach spaces with numerical index 1, Bull. London Math. Soc. 31 (1999), 207–212.CrossRefGoogle Scholar
Maksa, G. and Páles, Z., Wigner's theorem revisited, Publ. Math. Debrecen 81(12) (2012), 243–249.CrossRefGoogle Scholar
Mankiewicz, P., On extension of isometries in normed linear spaces, Bull. Acad. Polon, Sci. Set. Sci. Math. Astronomy, Phys. 20 (1972), 367–371.Google Scholar
Martín, M., Banach spaces having the Radon-Nikodým property and numerical index 1, Proc. Amer. Math. Soc. 131 (2003), 3407–3410.10.1090/S0002-9939-03-07176-4CrossRefGoogle Scholar
Martín, M. and Payá, R., On CL-spaces and almost CL-spaces, Ark. Mat. 42 (2004), 107–118.CrossRefGoogle Scholar
Mazur, S. and Ulam, S., Surles transformationes isométriques despaces vectoriels normés, C. R. Math. Acad. Sci. Paris 194 (1932), 946–948.Google Scholar
Molnár, L., Orthogonality preserving transformations on indefinite inner product spaces: generalization of Uhlhorn's version of Wigner's theorem, J. Funct. Anal. 194(2) (2002), 248–262.10.1006/jfan.2002.3970CrossRefGoogle Scholar
Mori, M., Tingley's problem through the facial structure of operator algebras, J. Math. Anal. Appl. 466(2) (2018), 1281–1298.10.1016/j.jmaa.2018.06.050CrossRefGoogle Scholar
Rätz, J., On Wigner's theorem: remarks, complements, comments, and corollaries, Aequationes Math. 52(1-2) (1996), 1–9.CrossRefGoogle Scholar
Reisner, S., Certain Banach spaces associated with graphs and CL-spaces with 1-unconditonal bases, J. London Math. Soc. (2) 43 (1991), 137–148.10.1112/jlms/s2-43.1.137CrossRefGoogle Scholar
Tan, D. and Huang, X., Phase-isometries on real normed spaces, J. Math. Anal. Appl. 488(1) (2020), 124058.10.1016/j.jmaa.2020.124058CrossRefGoogle Scholar
Tan, D., Huang, X. and Liu, R., Generalized-lush spaces and the Mazur-Ulam property, Studia Math. 219(2) (2013), 139–153.CrossRefGoogle Scholar
Tan, D. and Liu, R., A note on The Mazur-Ulam property of almost-CL-spaces, J. Math. Anal. Appl. 405 (2013), 336–341.CrossRefGoogle Scholar
Tanaka, R., A further property of spherical isometries, Bull. Austral. Math. Soc. 90(2) (2014), 304–310.CrossRefGoogle Scholar
Wigner, E., Gruppentheorie und ihre Anwendung auf die Quantenmechanik der Atomsprekten, (Braunschweig, Vieweg, 1931).CrossRefGoogle Scholar