Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-10T16:42:42.008Z Has data issue: false hasContentIssue false
  • English
  • Français

Self-adjoint extensions of bipartite Hamiltonians

Part of: Miscellaneous applications of functional analysis General mathematical topics and methods in quantum theory

Published online by Cambridge University Press:  22 June 2021

Daniel Lenz ,
Timon Weinmann  and
Melchior Wirth
Daniel Lenz
Affiliation:
Institute of Mathematics, Friedrich Schiller University Jena, Jena, Germany (daniel.lenz@uni-jena.de)
Timon Weinmann
Affiliation:
Department of Mathematics and Computer Science, St. Petersburg State University, St. Petersburg, Russia (st082214@student.spbu.ru)
Melchior Wirth
Affiliation:
Institute of Mathematics, Friedrich Schiller University Jena, Jena, Germany (melchior.wirth@ist.ac.at)
Get access Rights & Permissions [Opens in a new window]

Abstract

We compute the deficiency spaces of operators of the form $H_A{\hat {\otimes }} I + I{\hat {\otimes }} H_B$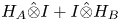, for symmetric $H_A$ 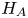and self-adjoint $H_B$. This enables us to construct self-adjoint extensions (if they exist) by means of von Neumann's theory. The structure of the deficiency spaces for this case was asserted already in Ibort et al. [Boundary dynamics driven entanglement, J. Phys. A: Math. Theor.47(38) (2014) 385301], but only proven under the restriction of $H_B$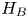 having discrete, non-degenerate spectrum.

Keywords

operator theoryfunctional analysismathematical physicsquantum systemsspectral theoryself-adjoint extensions

MSC classification

Primary: 46N50: Applications in quantum physics
Secondary: 81Q10: Selfadjoint operator theory in quantum theory, including spectral analysis
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 64 , Issue 3 , August 2021 , pp. 433 - 447
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

*

Address at the time of publication: IST Austria, Klosterneuburg, Austria.

References

Boitsev, A. A., Brasche, J. F., Malamud, M. M., Neidhardt, H. and Yu. Popov, I., Boundary triplets, tensor products and point contacts to reservoirs, Ann. Henri Poincaré 19(9) (2018), 2783–2837.CrossRefGoogle Scholar
Breuer, H.-P. and Petruccione, F., The theory of open quantum systems (Oxford University Press, New York, 2002).Google Scholar
Davies, E. B., Quantum theory of open systems (Academic Press [Harcourt Brace Jovanovich, Publishers], London-New York, 1976).Google Scholar
Ibort, A. and Pérez-Pardo, J. M., On the theory of self-adjoint extensions of symmetric operators and its applications to quantum physics, Int. J. Geometric Methods Mod. Phys. 12(6) (2015), 1560005–54.CrossRefGoogle Scholar
Ibort, A., Marmo, G. and Pérez-Pardo, J. M., Boundary dynamics driven entanglement, J. Phys. A: Math. Theor. 47(38) (2014), 385301.CrossRefGoogle Scholar
Schmüdgen, K., Unbounded self-adjoint operators on Hilbert space, Graduate Texts in Mathematics, Volume 265 (Springer, Dordrecht, 2012).CrossRefGoogle Scholar
Weidmann, J., Lineare Operatoren in Hilberträumen. Teil 1. Mathematische Leitfäden. [Mathematical textbooks] (Teubner, B. G., Stuttgart, Grundlagen, 2000).CrossRefGoogle Scholar