Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-10T10:07:42.580Z Has data issue: false hasContentIssue false
  • English
  • Français
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study when certain properties of Banach algebras are stable under ultrapower constructions. In particular, we consider when every ultrapower of 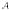is Arens regular, and give some evidence that this is so if and only if 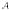is isomorphic to a closed subalgebra of operators on a super-reflexive Banach space. We show that such ideas are closely related to whether one can sensibly define an ultrapower of a dual Banach algebraffi We study how tensor products of ultrapowers behave, and apply this to study the question of when every ultrapower of 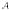is amenable. We provide an abstract characterization in terms of something like an approximate diagonal, and consider when every ultrapower of a C*-algebra, or a group L1-convolution algebra, is amenable.

Keywords

Banach algebraArens productsultrapoweramenabilitytensor product

MSC classification

Secondary: 46B08: Ultraproduct techniques in Banach space theory 46B28: Spaces of operators; tensor products; approximation properties 46H05: General theory of topological algebras 43A20: $L^1$-algebras on groups, semigroups, etc. 22D15: Group algebras of locally compact groups 47L10: Algebras of operators on Banach spaces and other topological linear spaces 46M05: Tensor products 46M07: Ultraproducts
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 52 , Issue 2 , June 2009 , pp. 307 - 338
Copyright
Copyright © Edinburgh Mathematical Society 2009