Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-10T09:13:33.124Z Has data issue: false hasContentIssue false
  • English
  • Français

An ideal-theoretic approach to Keller maps

Part of: Arithmetic rings and other special rings Affine geometry

Published online by Cambridge University Press:  11 June 2019

Cleto B. Miranda-Neto
Cleto B. Miranda-Neto*
Affiliation:
Departamento de Matemática, Universidade Federal da Paraíba, 58051-900 João Pessoa, PB, Brazil (cleto@mat.ufpb.br)
Get access Rights & Permissions [Opens in a new window]

Abstract

A self-map F of an affine space 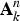${\bf A}_k^n $ over a field k is said to be a Keller map if F is given by polynomials F1, …, Fn ∈ k[X1, …, Xn] whose Jacobian determinant lies in 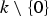$k\setminus \{0\}$. We consider char(k) = 0 and assume, as we may, that the Fis vanish at the origin. In this note, we prove that if F is Keller then its base ideal IF = 〈F1, …, Fn〉 is radical (a finite intersection of maximal ideals in this case). We then conjecture that IF = 〈X1, …, Xn〉, which we show to be equivalent to the classical Jacobian Conjecture. In addition, among other remarks, we observe that every complex Keller map admits a well-defined multidimensional global residue function.

Keywords

Keller mapJacobian Conjecturebase locusmultidimensional residue

MSC classification

Primary: 14R15: Jacobian problem 14R10: Affine spaces (automorphisms, embeddings, exotic structures, cancellation problem)
Secondary: 13F20: Polynomial rings and ideals; rings of integer-valued polynomials
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 62 , Issue 4 , November 2019 , pp. 1033 - 1044
Copyright
Copyright © Edinburgh Mathematical Society 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Abhyankar, S. S. and Moh, T.-T., Embeddings of the line in the plane, J. Reine Angew. Math. 276 (1975), 149–166.Google Scholar
2.Bakalarski, S., The irreducibility of symmetric Yagzhev maps, Proc. Amer. Math. Soc. 138 (2010), 2279–2281.Google Scholar
3.Bass, H., Connell, E. H. and Wright, D., The Jacobian Conjecture: reduction of degree and formal expansion of the inverse, Bull. Amer. Math. Soc. 7 (1982), 287–330.Google Scholar
4.Białynicki-Birula, A. and Rosenlicht, M., Injective morphisms of real algebraic varieties, Proc. Amer. Math. Soc. 13 (1962), 200–203.Google Scholar
5.Cattani, E., Dickenstein, A. and Sturmfels, B., Computing multidimensional residues, Progress in Mathematics, Volume 143 (Birkhäuser Verlag, Basel, 1996).Google Scholar
6.Cheng, C. C.-A., Power linear Keller maps of dimension four, J. Pure Appl. Algebra 169 (2002), 153–158.Google Scholar
7.Cheng, C. C.-A. and van den Essen, A., Endomorphisms of the plane sending linear coordinates to coordinates, Proc. Amer. Math. Soc. 128 (2000), 1911–1915.Google Scholar
8.Connell, E. H. and van den Dries, L., Injective polynomial maps and the Jacobian Conjecture, J. Pure Appl. Algebra 28 (1983), 235–239.Google Scholar
9.de Bondt, M., Polynomials with constant Hessian determinants in dimension three, J. Pure Appl. Algebra 219 (2015), 3743–3754.Google Scholar
10.de Bondt, M. and van den Essen, A., A reduction of the Jacobian Conjecture to the symmetric case, Proc. Amer. Math. Soc. 133 (2005), 2201–2205.Google Scholar
11.Dillen, F., Polynomials with constant Hessian determinant, J. Pure Appl. Algebra 71 (1991), 13–18.Google Scholar
12.Dolgachev, I., Polar Cremona transformations, Michigan Math. J. 48 (2000), 191–202.Google Scholar
13.Drużkowski, L. M., An effective approach to Keller's Jacobian Conjecture, Math. Ann. 264 (1983), 303–313.Google Scholar
14.Drużkowski, L. M., The Jacobian Conjecture: symmetric reduction and solution in the symmetric cubic linear case, Ann. Polon. Math. 87 (2005), 83–92.Google Scholar
15.Drużkowski, L. M. and Rusek, K., The formal inverse and the Jacobian Conjecture, Ann. Polon. Math. 46 (1985), 85–90.Google Scholar
16.Ein, L. and Shepherd-Barron, N., Some special Cremona transformations, Amer. J. Math. 111 (1989), 783–800.Google Scholar
17.Formanek, E., Two notes on the Jacobian Conjecture, Arch. Math. 49 (1987), 286–291.Google Scholar
18.Jedrzejewicz, P., A characterization of Keller maps, J. Pure Appl. Algebra 217 (2013), 165–171.Google Scholar
19.Jedrzejewicz, P. and Zieliński, J., Analogs of Jacobian conditions for subrings, J. Pure Appl. Algebra 221 (2017), 2111–2118.Google Scholar
20.Jedrzejewicz, P. and Zieliński, J., An approach to the Jacobian Conjecture in terms of irreducibility and square-freeness, Eur. J. Math. 3 (2017), 199–207.Google Scholar
21.Keller, O.-H., Ganze Cremona-Transformationen, Monatsh. Math. Phys. 47 (1939), 299–306.Google Scholar
22.Kunz, E., Kähler differentials, Advanced Lectures in Mathematics (Vieweg, Braunschweig, 1986).Google Scholar
23.Miranda-Neto, C. B., Tangential idealizers and differential ideals, Collect. Math. 67 (2016), 311–328.Google Scholar
24.Rusek, K., A geometric approach to Keller's Jacobian Conjecture, Math. Ann. 264 (1983), 315–320.Google Scholar
25.Valqui, C., Guccione, J. A. and Guccione, J. J., On the shape of possible counterexamples to the Jacobian Conjecture, J. Algebra 471 (2017), 13–74.Google Scholar
26.van den Essen, A., Polynomial automorphisms and the Jacobian Conjecture, Progress in Mathematics, Volume 190 (Birkhäuser Verlag, Basel, 2000).Google Scholar
27.van den Essen, A. and Zhao, W., On images of locally finite derivations and ε-derivations, J. Pure Appl. Algebra 223 (2019), 1689–1698.Google Scholar
28.Wang, S. S.-S., A Jacobian criterion for separability, J. Algebra 65 (1980), 453–494.Google Scholar
29.Yagzhev, A., On Keller's problem, Sib. Math. J. 21 (1980), 747–754.Google Scholar
30.Zhao, W., Hessian nilpotent polynomials and the Jacobian Conjecture, Trans. Amer. Math. Soc. 359 (2007), 249–274.Google Scholar