No CrossRef data available.
Published online by Cambridge University Press: 20 January 2009
An asymptotic expansion is given for the series
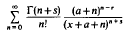
as x→∞ in the sector |Argx|≦π/2–δ. Here δ, Re(a), and Re(s) are positive and r is a positive integer. In the case a = r = s = 1, this yields the nontrivial result
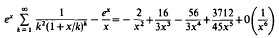
stated by Ramanujan in his notebooks [6].