No CrossRef data available.
Article contents
Baumslag–Solitar groups and residual nilpotence
Part of:
Structure and classification of infinite or finite groups
Special aspects of infinite or finite groups
Lie algebras and Lie superalgebras
Published online by Cambridge University Press: 16 June 2023
Abstract
Let G be a Baumslag–Solitar group. We calculate the intersection 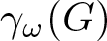 $\gamma_{\omega}(G)$ of all terms of the lower central series of G. Using this, we show that
$\gamma_{\omega}(G)$ of all terms of the lower central series of G. Using this, we show that 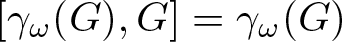 $[\gamma_{\omega}(G),G]=\gamma_{\omega}(G)$, thus answering a question of Bardakov and Neschadim [1]. For any
$[\gamma_{\omega}(G),G]=\gamma_{\omega}(G)$, thus answering a question of Bardakov and Neschadim [1]. For any 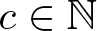 $c \in \mathbb{N}$, with
$c \in \mathbb{N}$, with 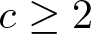 $c \geq 2$, we show, by using Lie algebra methods, that the quotient group
$c \geq 2$, we show, by using Lie algebra methods, that the quotient group 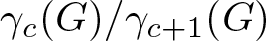 $\gamma_{c}(G)/\gamma_{c+1}(G)$ of the lower central series of G is finite.
$\gamma_{c}(G)/\gamma_{c+1}(G)$ of the lower central series of G is finite.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.
References
Bardakov, V. G. and Neshchadim, M. V., On the lower central series of Baumslag–Solitar groups, Algebra Logic 59 (2020), 281–294.10.1007/s10469-020-09601-zCrossRefGoogle Scholar
Baumslag, G. and Solitar, D., Some two-generator one-relator non-Hopfian groups, Bull. Amer. Math. Soc. 68 (1962), 199–201.10.1090/S0002-9904-1962-10745-9CrossRefGoogle Scholar
Bourbaki, N., Lie Groups and Lie Algebras Part I, Chapters 1–3 (Hermann, Paris, 1987).Google Scholar
Gruenberg, K. W., Residual properties of infinite soluble groups, Proc. Lond. Math. Soc. 7(3) (1957), 29–62.10.1112/plms/s3-7.1.29CrossRefGoogle Scholar
Kim, G. S. and McCarron, J., On amalgamated free products of residually p-finite groups, J. Algebra 162(1) (1993), 1–11.10.1006/jabr.1993.1237CrossRefGoogle Scholar
Lazard, M., Sur les groups nilpotents et les anneaux de Lie, Ann. Sci. Ec. Norm. Super. 71(3) (1954), 101–190.10.24033/asens.1021CrossRefGoogle Scholar
Levitt, G., Quotients and subgroups of Baumslag–Solitar groups, J. Group theory 18 (2015), 1–43.10.1515/jgth-2014-0028CrossRefGoogle Scholar
Meskin, S., Non-residually finite one-relator groups, Trans. Amer. Math. Soc. 164 (1972), 105–114.10.1090/S0002-9947-1972-0285589-5CrossRefGoogle Scholar
Moldavanskii, D. I., The intersection of the subgroups of finite p-index in Baumslag–Solitar groups, Vestnik Ivanovo State Univ. Ser. Natural Social Sci. 2 (2010), 106–111. (Russian).Google Scholar
Moldavanskii, D. I., The intersection of the subgroups of finite index in Baumslag–Solitar groups, Math. Notes 87(1) (2010), 88–95.10.1134/S0001434610010116CrossRefGoogle Scholar
Moldavanskii, D. I., On the residual properties of Baumslag–Solitar groups, Comm. Algebra 46(9) (2018), 3766–3778.10.1080/00927872.2018.1424867CrossRefGoogle Scholar
Raptis, E. and Varsos, D., Residual properties of HNN-extensions with base group an abelian group, J. Pure Appl. Algebra 59 (1989), 285–290.10.1016/0022-4049(89)90098-4CrossRefGoogle Scholar


