Hostname: page-component-686fd747b7-4b24c Total loading time: 0 Render date: 2025-02-13T11:00:41.699Z Has data issue: false hasContentIssue false
  • English
  • Français

The boundedness of the bilinear oscillatory integral along a parabola

Part of: Harmonic analysis in several variables

Published online by Cambridge University Press:  03 April 2023

Guoliang Li  and
Junfeng Li
Guoliang Li
Affiliation:
School of Mathematics and Statistics, Linyi University, Linyi, Shandong 276005, China (363621954@qq.com)
Junfeng Li
Affiliation:
School of Mathematical Sciences, Dalian University of Technology, Dalian, Liaoning 116024, China (junfengli@dlut.edu.cn)
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, the 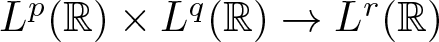$L^p(\mathbb{R})\times L^q(\mathbb{R})\rightarrow L^r(\mathbb{R})$ boundedness of the bilinear oscillatory integral along parabola

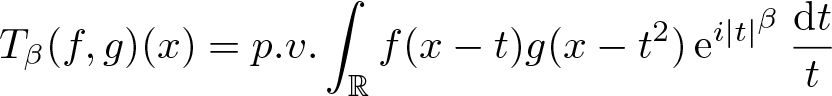\begin{equation*}T_\beta(f, g)(x)=p.v.\int_{{\mathbb R}} f(x-t)g(x-t^{2})\,{\rm e}^{i |t|^{\beta}}\,\frac{{\rm d}t}{t}\end{equation*}
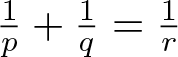is set up, where β > 1 or β < 0, $\frac{1}{p}+\frac{1}{q}=\frac{1}{r}$ and 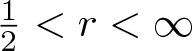$\frac{1}{2}\lt r\lt\infty$, p > 1 and q > 1. The result for the case β < 0 extends the 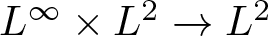$L^\infty\times L^2\to L^2$ boundedness obtained by Fan and Li (D. Fan and X. Li, A bilinear oscillatory integral along parabolas, Positivity 13(2) (2009), 339–366) by confirming an open question raised in it.

Keywords

bilinear operatoroscillatory integralstationary methodTT*methoddecay estimate

MSC classification

Primary: 42B37: Harmonic analysis and PDE 42B15: Multipliers
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 66 , Issue 1 , February 2023 , pp. 54 - 88
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Carleson, L., On convergence and growth of partial sums of Fourier series, Acta Math. 116 (1966), 125–157.10.1007/BF02392815CrossRefGoogle Scholar
Coifman, R. and Meyer, Y., On commutators of singular integrals and bilinear singular integrals, Trans. Amer. Math. Soc. 212 (1975), 315–331.10.1090/S0002-9947-1975-0380244-8CrossRefGoogle Scholar
Coifman, R. and Meyer, Y., Ondelettes et opéRatrs III. OpéRateurs multilineaires (Hermann, Paris, 1991).Google Scholar
Fan, D. and Li, X., A bilinear oscillatory integral along parabolas, Positivity 13(2) (2009), 339–366.10.1007/s11117-008-2270-3CrossRefGoogle Scholar
Fefferman, C., Pointwise convergence of Fourier series, Ann. Math. 98(2) (1973), 551–571.10.2307/1970917CrossRefGoogle Scholar
Fefferman, C. and Stein, E., H p spaces of several variables, Acta Math. 229(3–4) (1972), 137–193.10.1007/BF02392215CrossRefGoogle Scholar
I. Hirschman Jr., On multiplier transformations, Duke. Math. J. 26 (1959), 221–242.Google Scholar
Hörmander, L., Oscillatory integrals and multipliers on ${FL^p}$, Ark. Mat. 11 (1973), 1–11.10.1007/BF02388505CrossRefGoogle Scholar
Lacey, M. and Thiele, C., L p estimates on the bilinear Hilbert transform for $2 \lt p \lt \infty$, Ann. Math. 146 (1997), 693–724.10.2307/2952458CrossRefGoogle Scholar
Lacey, M. and Thiele, C., On Calderón’s conjecture, Ann. Math. 149(2) (1999), 475–496.10.2307/120971CrossRefGoogle Scholar
Li, X., Bilinear Hilbert transforms along curves I: the monomial case, Anal. PDE. 6(1) (2013), 197–220.10.2140/apde.2013.6.197CrossRefGoogle Scholar
Li, X. and Xiao, L., Uniform estimates for bilinear Hilbert transforms and bilinear maximal functions associated to polynomials, Amer. J. Math. 138(4) (2016), 907–962.10.1353/ajm.2016.0030CrossRefGoogle Scholar
Li, J. and Yu, H., Bilinear Hilbert transforms and (sub)bilinear maximal functions along convex curves, Pacific J. Math. 310(2) (2021), 375–446.10.2140/pjm.2021.310.375CrossRefGoogle Scholar
Phong, D. H. and Stein, E. M., On a stopping process for oscillatory integrals, J. Geom. Anal. 4 (1994), 104–120.10.1007/BF02921595CrossRefGoogle Scholar
Sjölin, P., Convolution with oscillating kernels, Indiana Univ. Math. J. 30(1) (1981), 47–55.10.1512/iumj.1981.30.30004CrossRefGoogle Scholar
Wainger, S., Special trigonometric series in k dimensions, Mem. Amer. Math Soc. 59 (1965).Google Scholar