Article contents
A Class of Homomorphism Theories for Groupoids
Published online by Cambridge University Press: 20 January 2009
Extract
In a well-behaved homomorphism theory for a class 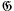 of algebraic systems certain “closed objects” relative to a given G ∈
of algebraic systems certain “closed objects” relative to a given G ∈ 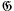 are distinguished which act as kernels of homomorphisms. For example, if
are distinguished which act as kernels of homomorphisms. For example, if 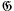 is the class of groups then the closed objects relative to a given group G are the normal subgroups of G; if
is the class of groups then the closed objects relative to a given group G are the normal subgroups of G; if 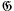 is the class of semigroups with zero element then one can devise a homomorphism theory in which the closed objects relative to a given S ∈
is the class of semigroups with zero element then one can devise a homomorphism theory in which the closed objects relative to a given S ∈ 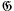 are the ideals of S[cf. Rees (3)]; in the class of groupoids one may define the closed objects relative to a given groupoid G to be the congruence relations on G, that is, subsets π⊆G×G which are equivalence relations having the property that (x1y1, x2y2) ∈ π whenever (x1, x2), (y1, y2) ∈ π. Given such a closed object N relative to G there exists a “factor” system G/N and a (canonical) homomorphism η: G→G/N characterised by the property: If σ G→H is a homomorphism with kernel N then there is a unique homomorphism
are the ideals of S[cf. Rees (3)]; in the class of groupoids one may define the closed objects relative to a given groupoid G to be the congruence relations on G, that is, subsets π⊆G×G which are equivalence relations having the property that (x1y1, x2y2) ∈ π whenever (x1, x2), (y1, y2) ∈ π. Given such a closed object N relative to G there exists a “factor” system G/N and a (canonical) homomorphism η: G→G/N characterised by the property: If σ G→H is a homomorphism with kernel N then there is a unique homomorphism 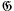 : G/N→H such that
: G/N→H such that 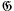 . η = σ and the kernel of
. η = σ and the kernel of 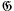 is trivial in the sense that the kernel of
is trivial in the sense that the kernel of 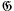 is the unique smallest closed object relative to G/N.
is the unique smallest closed object relative to G/N.
Information
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 14 , Issue 2 , December 1964 , pp. 129 - 135
- Copyright
- Copyright © Edinburgh Mathematical Society 1964
References
REFERENCES
- 2
- Cited by

