No CrossRef data available.
Article contents
Cohomology of a real toric variety and shellability of posets arising from a graph
Published online by Cambridge University Press: 03 November 2023
Abstract
Given a graph G without loops, the pseudograph associahedron PG is a smooth polytope, so there is a projective smooth toric variety XG corresponding to PG. Taking the real locus of XG, we have the projective smooth real toric variety 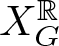 $X^{\mathbb{R}}_G$. The integral cohomology groups of
$X^{\mathbb{R}}_G$. The integral cohomology groups of 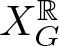 $X^{\mathbb{R}}_G$ can be computed by studying the topology of certain posets of even subgraphs of G; such a poset is neither pure nor shellable in general. We completely characterize the graphs whose posets of even subgraphs are always shellable. It follows that we get a family of projective smooth real toric varieties whose integral cohomology groups are torsion-free or have only 2-torsion.
$X^{\mathbb{R}}_G$ can be computed by studying the topology of certain posets of even subgraphs of G; such a poset is neither pure nor shellable in general. We completely characterize the graphs whose posets of even subgraphs are always shellable. It follows that we get a family of projective smooth real toric varieties whose integral cohomology groups are torsion-free or have only 2-torsion.
Keywords
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 66 , Issue 4 , November 2023 , pp. 1044 - 1084
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.



