Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-27T09:24:29.008Z Has data issue: false hasContentIssue false
  • English
  • Français

Compactness properties of critical nonlinearities and nonlinear Schrödinger equations

Part of: Partial differential equations Equations of mathematical physics and other areas of application

Published online by Cambridge University Press:  05 April 2013

David G. Costa ,
João Marcos do Ó  and
K. Tintarev
David G. Costa
Affiliation:
Department of Mathematical Sciences, University of Nevada Las Vegas, Box 454020, Las Vegas, NV 89154-4020, USA (costa@unlv.nevada.edu)
João Marcos do Ó
Affiliation:
Department of Mathematics, Universidade Federal de Paraiba, 58051-900 João Pessoa, PB, Brazil (jmbo@pq.cnpq.br)
K. Tintarev
Affiliation:
Department of Mathematics, Uppsala University, PO Box 480, 75106 Uppsala, Sweden (kyril.tintarev@math.uu.se)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove the compactness of critical Sobolev embeddings with applications to nonlinear singular Schrödinger equations and provide a unified treatment in dimensions N > 2 and N = 2, based on a somewhat unexpectedly broad array of parallel properties between spaces 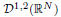and H10 of the unit disc. These properties include Leray inequality for N = 2 as a counterpart of Hardy inequality for N > 2, pointwise estimates by ground states r(2−N)/2 and 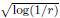of the respective Hardy-type inequalities, as well as compactness of the limiting Sobolev embeddings once the Sobolev norm is appended by a potential term whose growth at singularities exceeds that of the corresponding Hardy-type potential.

Keywords

Trudinger–Moser inequalityHardy inequalitycritical nonlinearitySchrödinger equationsingular potentials

MSC classification

Secondary: 35B33: Critical exponents 35B38: Critical points 35Q55: NLS-like equations (nonlinear Schrödinger)
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 56 , Issue 2 , June 2013 , pp. 427 - 441
Copyright
Copyright © Edinburgh Mathematical Society 2013

References

1.Adimurthi, J. M. do Ó and Tintarev, K., Cocompactness and minimizers for inequalities of Hardy–Sobolev type involving N-Laplacian, Nonlin. Diff. Eqns Applic. 17 (2010), 467–477.Google Scholar
2.Ambrosetti, A. and Rabinowitz, P. H., Dual variational methods in critical point theory and applications, J. Funct. Analysis 14 (1973), 349–381.CrossRefGoogle Scholar
3.Bennett, C. and Rudnick, K., On Lorentz–Zygmund spaces, Dissertationes Math. 175 (1980), 1–67.Google Scholar
4.Jeanjean, L. and Tanaka, K., A positive solution for a nonlinear Schrödinger equation on ℝN, Indiana Univ. Math. J. 54 (2005), 443–464.CrossRefGoogle Scholar
5.Leray, J., Sur le mouvement d'un liquide visqueux emplissant l'espace, Acta Math. 63 (1934), 193–248.CrossRefGoogle Scholar
6.Maz'ya, V., Sobolev spaces (Springer, 1985).Google Scholar
7.Moser, J., A sharp form of an inequality by N. Trudinger, Indiana Univ. Math. J. 20 (1971), 1077–1092.CrossRefGoogle Scholar
8.Ni, W. M., A nonlinear Dirichlet problem on the unit ball and its applications, Indiana Univ. Math. J. 31 (1982), 801–807.CrossRefGoogle Scholar
9.Solimini, S., A note on compactness-type properties with respect to Lorentz norms of bounded subsets of a Sobolev space, Annales Inst. H. Poincaré Analyse Non Linéaire 12 (1995), 319–337.CrossRefGoogle Scholar
10.Strauss, W. A., Existence of solitary waves in higher dimensions, Commun. Math. Phys. 55 (1977), 149–162.CrossRefGoogle Scholar
11.Su, J., Wang, Z.-Q. and Willem, M., Weighted Sobolev embedding with unbounded and decaying radial potentials, J. Diff. Eqns 238 (2007), 201–219.CrossRefGoogle Scholar
12.Su, J., Wang, Z.-Q. and Willem, M., Nonlinear Schrdinger equations with unbounded and decaying radial potentials, Commun. Contemp. Math. 9 (2007), 571–583.CrossRefGoogle Scholar
13.Tintarev, K., Cocompact embeddings and structure of weakly convergent sequences, in Sobolev Spaces in Mathematics (ed. Maz'ya, V. and Isakov, V.), Volume 1, International Mathematical Series, Volume 8, pp. 361–375 (Springer, 2009).CrossRefGoogle Scholar
14.Trudinger, N. S., On embeddings into Orlicz spaces and some applications, J. Math. Mech. 17 (1967), 473–483.Google Scholar