Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-02-03T23:34:32.493Z Has data issue: false hasContentIssue false
  • English
  • Français

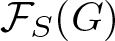Conditions for the supersolvability of $\mathcal{F}_{S}(G)$

Part of: Structure and classification of infinite or finite groups Representation theory of groups

Published online by Cambridge University Press:  23 January 2025

Guotuan Ru ,
Shengmin Zhang  and
Zhencai Shen
Guotuan Ru
Affiliation:
College of Science, China Agricultural University, Beijing, 100083 China
Shengmin Zhang
Affiliation:
College of Science, China Agricultural University, Beijing, 100083 China
Zhencai Shen*
Affiliation:
College of Science, China Agricultural University, Beijing, 100083 China
*
Corresponding author: Zhencai Shen, email: zhencai688@sina.com
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article, 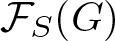$\mathcal{F}_{S}(G)$ denotes the fusion category of G on a Sylow p-subgroup S of G where p denotes a prime. A subgroup K of G has normal complement in G if there is a normal subgroup T of G satisfying that G = KT and 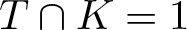$T \cap K = 1$. We investigate the supersolvability of 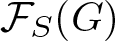$\mathcal{F}_{S}(G)$ under the assumption that some subgroups of S are normal in G or have normal complement in G.

Keywords

fusion systemnormal complement subgroupsupersolvable

MSC classification

Primary: 20D15: Nilpotent groups, $p$-groups 20C20: Modular representations and characters
Secondary: 20E45: Conjugacy classes
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , First View , pp. 1 - 7
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Asaad, M., Finite groups with certain subgroups of Sylow subgroups complemented, Journal of Algebra 323(7) (2010), 1958–1965.CrossRefGoogle Scholar
Aschbacher, M., Kessar, R. and Oliver, R., Fusion Systems in Algebra and Topology (New York: Cambridge University Press, 2011).CrossRefGoogle Scholar
Aseeri, F. and Kaspczyk, J., Criteria for supersolvability of saturated fusion systems, J. Algebra 647 (2024), 910–930.CrossRefGoogle Scholar
Bray, H. G. and Weinstein, M., Between Nilpotent and Solvable (Polygonal Publishing House, Passaic, New York, Jersey, 1982).Google Scholar
Cantarero, J., Scherer, J. and Viruel, A., Nilpotent p-local finite groups, Arkivför Matematik 52(3) (2014), 203–225.CrossRefGoogle Scholar
Craven, D. A., The Theory of Fusion Systems (Cambridge University Press, New York, 2011).CrossRefGoogle Scholar
Diaz, A., Glesser, A., Mazza, N. and Park, S.. Glaubermans and Thompsons theorems for fusion systems, Proceedings of the American Mathematical Society 137 (2) (2008) 495–503.CrossRefGoogle Scholar
Doerk, K. and Hawkes, T. O., Finite Soluble Groups (Berlin-New York: Walter de Gruyter, 2011).Google Scholar
Gorenstein, D., Finite Groups (Harper and Row Publishers, New York-Evanston-London, 1968).Google Scholar
Kessar, R. and Linckelmann, M., ZJ-theorems for fusion systems, Transactions of the American Mathematical Society 360(6) (2008), 3093–3106.CrossRefGoogle Scholar
Liao, J. and Liu, Y., Minimal non-nilpotent and locally nilpotent fusion systems, Algebra Colloquium 23(3) (2016), 455–462.CrossRefGoogle Scholar
Ru, G., Zhang, S. and Shen, Z. Complement and supplement properties on fusion systems FS(G).Google Scholar
Shen, Z., p-Nilpotent fusion systems, Journal of Algebra and Its Applications 17(12) (2018), .CrossRefGoogle Scholar
Shen, Z. and Zhang, J., p-supersolvable fusion systems (in Chinese), Scientia Sinica Mathematica 52(10) (2022), 1113–1120.Google Scholar
Zhang, S. and Shen, Z., Theorems of Szép, Zappa and Gaschütz for Fusion Systems (Submitted).Google Scholar