Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T09:51:17.329Z Has data issue: false hasContentIssue false
  • English
  • Français

Continuous flows generate few homeomorphisms

Part of: Connections with other structures, applications Smooth dynamical systems: general theory Topological dynamics Low-dimensional dynamical systems Maps and general types of spaces defined by maps

Published online by Cambridge University Press:  25 August 2020

Wescley Bonomo  and
Paulo Varandas
Wescley Bonomo
Affiliation:
Universidade Federal do Espírito Santo, CEUNES, Rodovia Governador Mario Covas, Km 60, S ao Mateus29.932-900, Brazil (wescley.bonomo@ufes.br)
Paulo Varandas
Affiliation:
Universidade Federal da Bahia, Av. Ademar de Barros s/n, Salvador40170-110, Brazil Universidade do Porto Faculdade de Ciências da Universidade do Porto, Rua do Campo Alegre s/n, Porto4169-007, Portugal (paulo.varandas@ufba.br)
Get access Rights & Permissions [Opens in a new window]

Abstract

We describe topological obstructions (involving periodic points, topological entropy and rotation sets) for a homeomorphism on a compact manifold to embed in a continuous flow. We prove that homeomorphisms in a 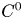$C^{0}$-open and dense set of homeomorphisms isotopic to the identity in compact manifolds of dimension at least two are not the time-1 map of a continuous flow. Such property is also true for volume-preserving homeomorphisms in compact manifolds of dimension at least five. In the case of conservative homeomorphisms of the torus 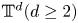$\mathbb {T}^{d} (d\ge 2)$ isotopic to identity, we describe necessary conditions for a homeomorphism to be flowable in terms of the rotation sets.

Keywords

Embedding problemflowable homeomorphismstopological entropyrotation sets

MSC classification

Primary: 37C10: Vector fields, flows, ordinary differential equations 54C25: Embedding 54H20: Topological dynamics
Secondary: 37B40: Topological entropy 37E30: Homeomorphisms and diffeomorphisms of planes and surfaces
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 63 , Issue 4 , November 2020 , pp. 971 - 983
Check for updates
Copyright
Copyright © The Author(s), 2020. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akin, E., Hurley, M. and Kennedy, J., Dynamics of topologically generic homeomorphisms, Mem. Amer. Math. Soc. 164(783) (2003), viii+130 pp.Google Scholar
Anderson, B., Diffeomorphisms with discrete centralizer, Topology 15 (1976), 143–147.CrossRefGoogle Scholar
Andrea, S., On homeomorphisms of the plane, and their embedding in flows, Bull. Amer. Math. Soc. 71 (1965), 381–383.CrossRefGoogle Scholar
Arbieto, A. and Matheus, C., A pasting lemma and some applications for conservative systems, Ergodic Th. Dynam. Sys. 27(5) (2007), 1399–1417.CrossRefGoogle Scholar
Arnaud, M.-C., Le “closing lemma” en topologie $C^{1}$, Mém. Soc. Math. Fr. 74 (1998), vi+120 p.Google Scholar
Bessa, M., Torres, M. J. and Varandas, P., On the periodic orbits, shadowing and strong transitivity of continuous flows, Nonlinear Anal. 175 (2018), 191–209.CrossRefGoogle Scholar
Bonomo, W., Lima, H. and Varandas, P., The rotation sets of most homeomorphisms on $\mathbb {T}^{d}$ are stable, convex and rational polyhedrons, Isr. J. Math. (to appear).Google Scholar
Brin, M., The inclusion of a diffeomorphism into a flow, Izv. Vyss. Ucebn. Zaved. Matematika 8(123) (1972), 19–25.Google Scholar
Edwards, R. D. and Kirby, R. C., Deformations of spaces of embeddings, Ann. Math. 93(2) (1971), 63–88.CrossRefGoogle Scholar
Foland, N. E., An embedding theorem for discrete flows on a closed 2-cell, Duke Math. J. 33 (1966), 441–444.CrossRefGoogle Scholar
Fort, M. K., The embedding of homeomorphisms in flows, Proc. Amer. Math. Soc. 6 (1955), 960–967.CrossRefGoogle Scholar
Franks, J., Necessary conditions for stability of diffeomorphisms, Trans. Amer. Math. Soc. 158(2) (1971), 301–308.CrossRefGoogle Scholar
Franks, J. and Misiurewicz, M., Rotation sets of toral flows, Proc. Amer. Math. Soc. 109(1) (1990), 243–249.CrossRefGoogle Scholar
Grines, V., Gurevich, E., Medvedev, V. and Pochinka, O., On embedding a Morse-Smale diffeomorphism on a 3-manifold in a topological flow, Sbornik Math. 203(12) (2012), 1761.CrossRefGoogle Scholar
Guihéneuf, P.-A., Proprietés dynamiques genériques des homéomorphismes conservatifs, Ensaios Matemáticos, Volume 22 (Sociedade Brasileira de Matemática, 2012).Google Scholar
Guzik, G., Cocycles and continuous iteration semigroups of triangular functions, J. Difference Equ. Appl. 21(12) (2015), 1171–1185.CrossRefGoogle Scholar
Hurley, M., On proof of the $C^{0}$-general density theorem, Proc. Amer. Math. Soc. 124(4) (1996), 1305–1309.CrossRefGoogle Scholar
Kopell, N., Commuting diffeomorphisms. in Global analysis, Proceedings of Symposia in Pure Mathematics XIV, pp. 165–184 (Berkeley, CA, 1968).CrossRefGoogle Scholar
Le Roux, F., O'Farrell, A., Roginskaya, M. and Short, I., Flowability of plane homeomorphisms, Ann. Inst. Fourier 62(2) (2012), 619–639.CrossRefGoogle Scholar
Misiurewicz, M. and Ziemian, K., Rotation sets for maps of tori, J. London Math. Soc. (2) 40(3) (1989), 490–506.CrossRefGoogle Scholar
Müller, S., Uniform approximation of homeomorphisms by diffeomorphisms, Topology Appl. 178 (2014), 315–319.CrossRefGoogle Scholar
Munkres, J., Obstructions to the smoothing of piecewise-differentiable homeomorphisms, Ann. Math. 72 (1960), 521–554.CrossRefGoogle Scholar
Oh, Y.-G., $C^{0}$-coerciveness of Moser's Problem and smoothing area-preserving homeomorphisms, arXiv:math/0601183.Google Scholar
Palis, J., Vector fields generate few diffeomorphisms, Bull, Amer. Math. Soc. 80(3) (1974), 503–505.CrossRefGoogle Scholar
Passeggi, A., Rational polygons as rotation sets of generic homeomorphisms of the two torus, J, Lond. Math. Soc. (2) 89(1) (2014), 235–254.CrossRefGoogle Scholar
Polterovich, L. and Shelukhin, E., Autonomous Hamiltonian flows, Hofer's geometry and persistence modules, Sel. Math. New Ser. 22 (2016), 227–296.CrossRefGoogle Scholar
Pugh, C. and Robinson, C., The $C^{1}$-Closing Lemma, including Hamiltonians, Ergodic Th. Dynam. Sys. 3 (1983), 261–313.CrossRefGoogle Scholar
Sikorav, J.-C., Approximation of a volume-preserving homeomorphism by a volume-preserving diffeomorphism, available at http://www.umpa.ens-lyon.fr/symplexe (September 2007).Google Scholar
Teixeira, P., On the conservative pasting lemma, Ergodic Th. Dynam. Sys. 40(5) (2020), 1402–1440.CrossRefGoogle Scholar
Togawa, Y., Generic Morse-Smale diffeomorphisms have only trivial symmetries, Proc. Amer. Math. Soc. 65(1) (1977), 145–149.CrossRefGoogle Scholar
Utz, W., The embedding of homeomorphisms in continuous flows, The Proceedings of the 1981 Topology Conference (Blacksburg, VA, 1981). Topology Proc. 6(1) (1982), 159–177Google Scholar
Yano, K., A remark on the topological entropy of homeomorphisms, Invent. Math. 59 (1980), 215–220.CrossRefGoogle Scholar
Young, L.-S., Entropy of continuous flows on compact 2-manifolds, Topology 16 (1977), 469–471.CrossRefGoogle Scholar
Zdun, M., On embedding of homeomorphisms of the circle in a continuous flow. Iteration theory and its functional equations, Lecture Notes in Math., Volume 1163, pp. 218–231 (Springer, Berlin, 1985)CrossRefGoogle Scholar