Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-10T19:32:56.239Z Has data issue: false hasContentIssue false
  • English
  • Français

Crystal flex bases and the RUM spectrum

Part of: Discrete geometry Phase transformations in solids

Published online by Cambridge University Press:  24 November 2021

G. Badri ,
D. Kitson Open the ORCID record for D. Kitson [Opens in a new window]  and
S. C. Power Open the ORCID record for S. C. Power [Opens in a new window]
G. Badri
Affiliation:
Department of Mathematical Sciences, Umm Al-Qura University, Mecca Saudi Arabia (gmbadri@uqu.edu.sa)
D. Kitson
Affiliation:
Department of Mathematics and Computer Studies, Mary Immaculate College, Thurles, Co. Tipperary, Ireland (derek.kitson@mic.ul.ie)
S. C. Power
Affiliation:
Department of Mathematics and Statistics, Lancaster University, LancasterLA1 4YF, UK (s.power@lancaster.ac.uk)
Get access Rights & Permissions [Opens in a new window]

Abstract

A theory of infinite spanning sets and bases is developed for the first-order flex space of an infinite bar-joint framework, together with space group symmetric versions for a crystallographic bar-joint framework ${{\mathcal {C}}}$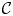. The existence of a crystal flex basis for ${{\mathcal {C}}}$ 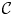is shown to be closely related to the spectral analysis of the rigid unit mode (RUM) spectrum of ${{\mathcal {C}}}$ 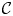and an associated geometric flex spectrum. Additionally, infinite spanning sets and bases are computed for a range of fundamental crystallographic bar-joint frameworks, including the honeycomb (graphene) framework, the octahedron (perovskite) framework and the 2D and 3D kagome frameworks.

Keywords

rigid unit modesperiodic frameworksflexibility

MSC classification

Primary: 52C25: Rigidity and flexibility of structures 74N05: Crystals
Secondary: 74N10: Displacive transformations
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 64 , Issue 4 , November 2021 , pp. 735 - 761
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Badri, G., Kitson, D. and Power, S. C., The almost periodic rigidity of crystallographic bar-joint frameworks, Symmetry 6 (2014), 308–328.CrossRefGoogle Scholar
Connelly, R., Ivić, W. A. and Whiteley, W., Rigidity and symmetry, Fields Institute Communications, Volume 70 (Springer, 2014).CrossRefGoogle Scholar
Dove, M. T., Heine, V. and Hammonds, K. D., Rigid unit modes in framework silicates, Mineral. Mag. 59 (1995), 629–639.CrossRefGoogle Scholar
Dove, M. T., Pryde, A. K. A., Heine, V. and Hammonds, K. D., Exotic distributions of rigid unit modes in the reciprocal spaces of framework aluminosilicates, J. Phys. Condens. Matter 19 (2007), 275209. doi:10.1088/0953-8984/19/27/275209CrossRefGoogle Scholar
Giddy, A. P., Dove, M. T., Pawley, G. S. and Heine, V., The determination of rigid unit modes as potential soft modes for displacive phase transitions in framework crystal structures, Acta Crystallogr. A49 (1993), 697–703.CrossRefGoogle Scholar
Graf, G. M. and Porta, M., Bulk-edge correspondence for two-dimensional topological insulators, Comm. Math. Phys. 324 (2013), 851–895.CrossRefGoogle Scholar
Guest, S. D., Fowler, P. W. and Power, S. C., (Editors), Rigidity of periodic and symmetric structures in nature and engineering, Phil. Trans. R. Soc. A 372 (2014), 0358.CrossRefGoogle ScholarPubMed
Hutchinson, R. G. and Fleck, N. A., The structural performance of the periodic truss, J. Mech. Phys. Solids 54 (2006), 756–782.CrossRefGoogle Scholar
Kasim Sait, A., Rigidity of Infinite Frameworks, MPhil thesis, Lancaster University (2011).Google Scholar
Kastis, E. and Power, S. C., Algebraic spectral synthesis and crystal rigidity, J. Pure Appl. Algebra 223 (2019), 4954–4965.CrossRefGoogle Scholar
Kastis, E. and Power, S. C., The first-order flexibility of a crystal framework, J. Math. Anal. App. 504 (2021), 125404. doi:10.1016/j.jmaa.2021.125404CrossRefGoogle Scholar
Kitson, D. and Power, S. C., The rigidity of infinite graphs, Discrete Comput. Geom. 60 (2018), 531–557.CrossRefGoogle Scholar
Lubensky, T. C., Kane, C. L., Mao, X., Souslov, A. and Sun, K., Phonons and elasticity in critically coordinated lattices, Rep. Progress Phys. 78(7) (2015), 073901.CrossRefGoogle ScholarPubMed
Owen, J. C. and Power, S. C., Infinite bar-joint frameworks, crystals and operator theory, New York J. Math. 17 (2011), 445–490.Google Scholar
Power, S. C., Polynomials for crystal frameworks and the rigid unit mode spectrum, Phil. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 372 (2014), 20120030.Google ScholarPubMed
Rocklin, D. Z., Gin-ge Chen, B., Falk, M., Vitelli, V. and Lubensky, T. C., Mechanical Weyl modes in topological Maxwell lattices, Phys. Rev. Lett. 116 (2016), 135503.CrossRefGoogle ScholarPubMed
Wegner, F., Rigid-unit modes in tetrahedral crystals, J. Phys. Condens. Matter 19 (2007), 406218. doi:10.1088/0953-8984/19/40/406218CrossRefGoogle ScholarPubMed