Equal Sums of Like Powers

Extract

In this note all small latin letters denote rational integers. We write k ≧ 1, s ≧ 1 and consider the simultaneous equations

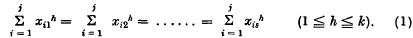
A solution of these equations is said to be non-trivial if no set {x_iu} is a permutation of another set {x_iv}. In 1851 Prouhet constructed a non-trivial solution of these equations with j = s^k and Lehmer has recently found a parametric solution for the same j. Here I give two alternative elementary proofs of Lehmer's result. Lehmer's own proof depends on the ideas of generating functions, exponentials, differentiation, matrices, and complex roots of unity, though all at a fairly simple level. One of my proofs requires only the factor theorem for a polynomial and the other only the multinomial theorem for a positive integral index.