Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Frei, Christopher
Loughran, Daniel
and
Sofos, Efthymios
2018.
Rational points of bounded height on general conic bundle surfaces.
Proceedings of the London Mathematical Society,
Vol. 117,
Issue. 2,
p.
407.
Huang, Zhizhong
and
Montero, Pedro
2020.
Fano Threefolds as Equivariant Compactifications of the Vector Group.
Michigan Mathematical Journal,
Vol. 69,
Issue. 2,
Pieropan, Marta
Smeets, Arne
Tanimoto, Sho
and
Várilly‐Alvarado, Anthony
2021.
Campana points of bounded height on vector group compactifications.
Proceedings of the London Mathematical Society,
Vol. 123,
Issue. 1,
p.
57.
Arzhantsev, Ivan
and
Zaitseva, Yulia Ivanovna
2022.
Эквивариантные пополнения аффинных пространств.
Успехи математических наук,
Vol. 77,
Issue. 4(466),
p.
3.
Arzhantsev, Ivan
and
Zaitseva, Yulia Ivanovna
2022.
Equivariant completions of affine spaces.
Russian Mathematical Surveys,
Vol. 77,
Issue. 4,
p.
571.
Derenthal, Ulrich
and
Wilsch, Florian
2024.
INTEGRAL POINTS ON SINGULAR DEL PEZZO SURFACES.
Journal of the Institute of Mathematics of Jussieu,
Vol. 23,
Issue. 3,
p.
1259.
Ortmann, Judith
2024.
Integral points on a del Pezzo surface over imaginary quadratic fields.
Research in Number Theory,
Vol. 10,
Issue. 4,


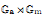 on ℙ
on ℙ