Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Yalçın, Ergün
2016.
Rank 3 finitep-group actions on products of spheres.
Bulletin of the London Mathematical Society,
Vol. 48,
Issue. 2,
p.
325.

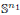 × … ×
× … × 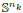 for some positive integers
for some positive integers 