Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-10T12:16:21.242Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalised Algebraic Continued Fractions related to Definite Integrals1

Published online by Cambridge University Press:  20 January 2009

L. R. Shenton
L. R. Shenton
Affiliation:
Manchester College of Science and Technology, Manchester, 1.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The present paper is a continuation of the work initiated in [l]-[5]. In [5] I gave an expansion of the form

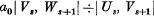
for the second order C.F. associated with

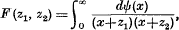
where U8, V8, W8 satisfy a fourth-order recurrence relation, there being a similar expansion for third order C.F.'s. I shall now give simple expressions for U8, V8, W8 (or related forms) in terms of χ2s(Z1), χ2s (Z2), ω2s(Z1), ω2s(Z2), where

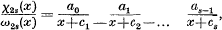
and show that there is a remarkable relation between the recurrence formula for the first order C.F. and that satisfied by U3, V3, W3. The generalised form of these results will be stated and proved.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 9 , Issue 4 , May 1958 , pp. 170 - 182
Copyright
Copyright © Edinburgh Mathematical Society 1958

References

REFERENCES

1.Shenton, L. R., Proc. Edinburgh Math. Soc. (2), 9 (1953), 44–52.CrossRefGoogle Scholar
2.Shenton, L. R., Proc. Edinburgh Math. Soc. (2), 10 (1954), 78–91.CrossRefGoogle Scholar
3.Shenton, L. R., Proc. Edinburgh Math. Soc. (2), 10 (10), 134–140.CrossRefGoogle Scholar
4.Shenton, L. R., Proc. Edinburgh Math. Soc. (2), 10 (1957), 153–166.CrossRefGoogle Scholar
5.Shenton, L. R., Proc. Edinburgh Math. Soc. (2), 10 (1957), 167–188.CrossRefGoogle Scholar
6.Jacobi, C. G. J., Crelle's Journal, lxix (1868), 29–64.Google Scholar
7.Hermite, Ch., Annali di Mat. (2), 21 (1893), 289–308.CrossRefGoogle Scholar
8.Perron, O., Math. Annalen, 64 (1907), 1–76.CrossRefGoogle Scholar
9.Bateman, H., Quart. J. Math., xli (1910), 302–308.Google Scholar
10.Paley, R. E. A. C. and Ursell, H. D., Proc. Cambridge Phil. Soc., 26 (1929), 127–144.CrossRefGoogle Scholar
11.Stieltjes, and Hermite, , Correspondance d'Hermite et de Stieltjes, Vols. 1 and 2 (Paris, 1905: Gauthier-Villars).Google Scholar