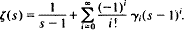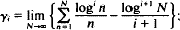Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Berndt, Bruce C
and
Evans, Ronald J
1983.
Chapter 7 of Ramanujan’s second notebook.
Proceedings of the Indian Academy of Sciences - Section A,
Vol. 92,
Issue. 2,
Balakrishnan, U.
1986.
Laurent expansion of Dirichlet series.
Bulletin of the Australian Mathematical Society,
Vol. 33,
Issue. 3,
p.
351.
Balakrishnan, U.
1987.
Laurent expansion of Dirichlet series-II.
Monatshefte f�r Mathematik,
Vol. 103,
Issue. 1,
p.
1.
Dilcher, Karl
1992.
Generalized Euler constants for arithmetical progressions.
Mathematics of Computation,
Vol. 59,
Issue. 199,
p.
259.
Ishibashi, Makoto
and
Kanemitsu, Shigeru
1999.
Dirichlet series with periodic coefficients.
Results in Mathematics,
Vol. 35,
Issue. 1-2,
p.
70.
Shirasaka, S.
2002.
On the Laurent coefficients of a class of Dirichlet series.
Results in Mathematics,
Vol. 42,
Issue. 1-2,
p.
128.
Ishikawa, H.
and
Thuswaldner, J. M.
2004.
On the asymptotic behavior of the Laurent coefficients of a class of Dirichlet series.
Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg,
Vol. 74,
Issue. 1,
p.
11.
Kanemitsu, S.
Kumagai, H.
Srivastava, H.M.
and
Yoshimoto, M.
2004.
Some integral and asymptotic formulas associated with the Hurwitz Zeta function.
Applied Mathematics and Computation,
Vol. 154,
Issue. 3,
p.
641.
Atkinson, Bruce W.
2012.
Meromorphic representations of products of complex arithmetic progressions.
Aequationes mathematicae,
Vol. 83,
Issue. 3,
p.
295.
Saad Eddin, Sumaia
2013.
Explicit upper bounds for the Stieltjes constants.
Journal of Number Theory,
Vol. 133,
Issue. 3,
p.
1027.
Chatterjee, Tapas
and
Khurana, Suraj Singh
2019.
Shifted Euler constants and a generalization of Euler-Stieltjes constants.
Journal of Number Theory,
Vol. 204,
Issue. ,
p.
185.
Wang, N.-L.
Agarwal, Praveen
and
Kanemitsu, S.
2020.
Limiting Values and Functional and Difference Equations.
Mathematics,
Vol. 8,
Issue. 3,
p.
407.
WANG, Xiaohan
MEHTA, Jay
and
KANEMITSU, Shigeru
2020.
THE BOUNDARY LERCH ZETA-FUNCTION AND SHORT CHARACTER SUMS À LA Y. YAMAMOTO.
Kyushu Journal of Mathematics,
Vol. 74,
Issue. 2,
p.
313.
Chatterjee, Tapas
and
Khurana, Suraj Singh
2022.
A series representation of Euler–Stieltjes constants and an identity of Ramanujan.
Rocky Mountain Journal of Mathematics,
Vol. 52,
Issue. 1,
Chatterjee, Tapas
and
Garg, Sonam
2023.
On 𝑞-analogue of Euler–Stieltjes constants.
Proceedings of the American Mathematical Society,
Languasco, Alessandro
and
Moree, Pieter
2025.
Euler constants from primes in arithmetic progression.
Mathematics of Computation,