No CrossRef data available.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Published online by Cambridge University Press: 20 January 2009
The hypergeometric function1F(a, b; c; z) is analytic in the domain |arg(−z)| < π, and, when |z| < 1, may be represented by the series
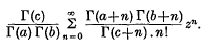
When |z| = 1 in the domain |arg(−z)| <π, this series converges2 to F(a; b; c; z) if R(a+b−c) < 0 (integral values of a, b and c are excluded in the present paper).
1 Whittaker, and Watson, , Modern Analysis (1927), Ch. XIV.Google Scholar
2 Ibid., pp. 25 and 57.
3 Fabian, , Quart. J. of Math., 7 (1936), 252. CJ. the Riemann-Liouville integral.CrossRefGoogle Scholar
1 Fabian, , Math. Gazette, 20 (1936), 249.CrossRefGoogle Scholar
2 Whittaker, and Watson, , op. cit., p. 23.Google Scholar
1 Fabian, , Math. Gazette, 20 (1936), 249.CrossRefGoogle Scholar
You have
Access