Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Smith, Kirby C.
1986.
The group of units of a gc near-ring.
Communications in Algebra,
Vol. 14,
Issue. 9,
p.
1809.
Pettet, Martin R.
and
Smith, Kirby C.
1989.
Distributively generated gc near-rings.
Communications in Algebra,
Vol. 17,
Issue. 6,
p.
1505.
Bagley, Scott W
1997.
Distributor and j2-radical ideals of generalized centralizer near-rings.
Communications in Algebra,
Vol. 25,
Issue. 11,
p.
3405.

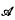 be a group of automorphisms of
be a group of automorphisms of 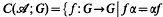 for all α∈
for all α∈