Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T16:30:32.207Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalized manifolds, normal invariants, and 𝕃-homology

Part of: Generalized manifolds Classical Topics in Algebraic Topology Differential topology Homology and cohomology theories Fiber spaces and bundles Categories and geometry

Published online by Cambridge University Press:  16 June 2021

Friedrich Hegenbarth  and
Dušan Repovš
Friedrich Hegenbarth
Affiliation:
Dipartimento di Matematica ‘Federigo Enriques’, Università degli studi di Milano, 20133Milano, Italy (friedrich.hegenbarth@unimi.it)
Dušan Repovš
Affiliation:
Faculty of Education and Faculty of Mathematics and Physics, University of Ljubljana, 1000Ljubljana, Slovenia (dusan.repovs@guest.arnes.si)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let $X^{n}$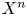 be an oriented closed generalized $n$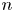-manifold, $n\ge 5$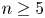. In our recent paper (Proc. Edinb. Math. Soc. (2) 63 (2020), no. 2, 597–607), we have constructed a map $t:\mathcal {N}(X^{n}) \to H^{st}_{n} ( X^{n}; \mathbb{L}^{+})$ which extends the normal invariant map for the case when $X^{n}$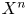 is a topological $n$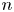-manifold. 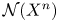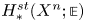Here, $\mathcal {N}(X^{n})$ denotes the set of all normal bordism classes of degree one normal maps $(f,\,b): M^{n} \to X^{n},$ and $H^{st}_{*} ( X^{n}; \mathbb{E})$ denotes the Steenrod homology of the spectrum $\mathbb{E}$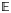. An important non-trivial question arose whether the map $t$ 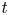is bijective (note that this holds in the case when $X^{n}$ 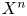is a topological $n$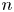-manifold). It is the purpose of this paper to prove that the answer to this question is affirmative.

Keywords

Generalized manifoldSteenrod $\mathbb{L}$-homologyPoincaré duality complexnormal invariant of degree one mapperiodic surgery spectrum $\mathbb{L}$fundamental complexSpivak fibrationPontryagin–Thom constructionSpanier–Whitehead dualityabsolute neighbourhood retract

MSC classification

Primary: 55N07: Steenrod-Sitnikov homologies 55R20: Spectral sequences and homology of fiber spaces 57P10: Poincaré duality spaces 57R67: Surgery obstructions, Wall groups
Secondary: 18F15: Abstract manifolds and fiber bundles 55M05: Duality 55N20: Generalized (extraordinary) homology and cohomology theories 57P05: Local properties of generalized manifolds 57P99: None of the above, but in this section 57R65: Surgery and handlebodies
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 64 , Issue 3 , August 2021 , pp. 574 - 589
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Dedicated to the memory of Professor Erik Kjær Pedersen (1946–2020)

References

Browder, W., Surgery on simply-connected manifolds, Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 65 (Springer-Verlag, Heidelberg, 1972), MR 0358813.10.1007/978-3-642-50020-6CrossRefGoogle Scholar
Bryant, J. L., Ferry, S., Mio, W. and Weinberger, S., Topology of homology manifolds, Ann. of Math. 143(2) (1996), 435–467, MR 1394965.10.2307/2118532CrossRefGoogle Scholar
Cavicchioli, A., Hegenbarth, F. and Repovš, D., Higher-dimensional generalized manifolds: surgery and constructions, EMS Series of Lectures in Mathematics, Volume 23 (European Math. Soc., Zürich, 2016), MR 3558558.10.4171/156CrossRefGoogle Scholar
Ferry, S. C., Geometric topology notes (Piscataway, NJ, Rutgers University, 1992–1993), https://sites.math.rutgers.edu/~sferry/ps/geotop.pdf.Google Scholar
Ferry, S. C., Remarks on Steenrod homology, in Novikov conjectures, index theorems, and rigidity, Volume 2 (eds. S. Ferry, A. Ranicki, and J. Rosenberg), London Math. Soc. Lecture Note Ser., Volume 227, pp. 148–166 (Cambridge University Press, Cambridge, 1995), MR 1388310.CrossRefGoogle Scholar
Ferry, S. C. and Pedersen, E. K., Epsilon surgery theory, in Novikov conjecture, index theorem and rigidity Volume 2 (eds. S. Ferry, A. Ranicki, and J. Rosenberg), pp. 167–226, London Math. Soc. Lecture Notes Series, Volume 227 (London, 1995), MR 1388311.Google Scholar
Hausmann, J. C. and Vogel, P., Geometry on Poincaré spaces, Math. Notes, Volume 41 (Princeton University Press, Princeton, NJ, 1993), MR 1238937.Google Scholar
Hegenbarth, F. and Repovš, D., The Bryant-Ferry-Mio-Weinberger construction of generalized manifolds, in Exotic homology manifolds, Oberwolfach 2003, pp. 17–32, Geom. Topol. Monogr., Volume 9, (Geom. Topol. Publ., Coventry, 2006), MR 2222488.Google Scholar
Hegenbarth, F. and Repovš, D., On Steenrod $\mathbb {L}$-homology, generalized manifolds, and surgery, Proc. Edinb. Math. Soc. 63(2) (2020), 579–607, MR 4085040.Google Scholar
Kahn, D. S., Kaminker, J. and Schochet, C., Generalized homology theories on compact metric spaces, Michigan Math. J. 24(2) (1977), 203–224, MR 0474274.CrossRefGoogle Scholar
Kirby, R. C. and Siebenmann, L. C., Foundational essays on topological manifolds, smoothings, and triangulations, With notes by J. Milnor and M. Atiyah, Ann. of Math. Stud., Volume 88 (Princeton University Press, Princeton, NJ, 1977), MR 0645390.10.1515/9781400881505CrossRefGoogle Scholar
Kühl, P., Macko, T. and Mole, A., The total surgery obstruction revisited, Münster J. Math. 6(1) (2013), 181–269, MR 3148212.Google Scholar
Levitt, N., Poincaré duality cobordism, Ann. of Math. (2) 96 (1972), 211–244, MR 0314059.10.2307/1970787CrossRefGoogle Scholar
Madsen, I. and Milgram, R. J., The classifying spaces for surgery and cobordism of manifolds, Ann. of Math. Stud., Volume 92 (Princeton University Press, Princeton, NJ, 1979), MR 0548575.Google Scholar
Milnor, J., On the Steenrod homology theory, in Novikov conjectures, index theorems, and rigidity, Volume 1 (eds. S. Ferry, A. Ranicki, and J. Rosenberg), pp. 79–96, London Math. Soc. Lecture Note Ser., Volume 226 (Cambridge University Press, Cambridge, 1995), MR 1388297.Google Scholar
Mio, W., Homology manifolds, in Surveys on surgery theory, Volume 1: Papers Dedicated to C. T. C. Wall (eds. S. Cappell, A. Ranicki and J. Rosenberg), pp. 323–343, Ann. of Math. Stud., Volume 145, (Princeton University Press, Princeton, NJ, 2000), MR 1747540.Google Scholar
Nicas, A., Induction theorems for groups of homotopy manifold structures, Mem. Amer. Math. Soc., Volume 39 (267) (Amer. Math. Soc., Providence, RI, 1982), MR 0668807.10.1090/memo/0267CrossRefGoogle Scholar
Quinn, F. S., Surgery on Poincaré and normal spaces, Bull. Amer. Math. Soc. 78 (1972), 262–267, MR 0296955.10.1090/S0002-9904-1972-12950-1CrossRefGoogle Scholar
Ranicki, A. A., The total surgery obstruction, in Proc. Alg. Topol. Conf. Aarhus 1978, pp. 275–316, Lect. Notes Math., Volume 763 (Springer-Verlag, Berlin, 1979), MR 0561227.Google Scholar
Ranicki, A. A., Algebraic L-theory and topological manifolds, Cambridge Tracts in Math., Volume 102 (Cambridge University Press, Cambridge, 1992), MR 1211640.Google Scholar
Ranicki, A. A., A composition formula for manifold structures, Pure Appl. Math. Q. 5(2) (2009), 701–727, MR 2508900.10.4310/PAMQ.2009.v5.n2.a5CrossRefGoogle Scholar
Wall, C. T. C., Surgery on compact manifolds, 2nd Ed., Edited and with a foreword by A. A. Ranicki, Mathematical Surveys and Monographs, Volume 69 (Amer. Math. Soc., Providence, RI, 1999), MR 1687388.10.1090/surv/069CrossRefGoogle Scholar