Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Maróti, Attila
2016.
A lower bound for the number of conjugacy classes of a finite group.
Advances in Mathematics,
Vol. 290,
Issue. ,
p.
1062.
Maróti, Attila
and
Simion, Iulian I.
2020.
Bounding the number of classes of a finite group in terms of a prime.
Journal of Group Theory,
Vol. 23,
Issue. 3,
p.
471.
Hung, Nguyen Ngoc
and
Maróti, Attila
2022.
p-Regular conjugacy classes and p-rational irreducible characters.
Journal of Algebra,
Vol. 607,
Issue. ,
p.
387.
Nguyen, Ngoc Hung
and
Schaeffer Fry, A. A.
2023.
On Héthelyi–Külshammer’s conjecture for
principal blocks.
Algebra & Number Theory,
Vol. 17,
Issue. 6,
p.
1127.
Hung, Nguyen N.
Schaeffer Fry, A.A.
and
Vallejo, Carolina
2024.
Principal blocks with six ordinary irreducible characters.
Journal of Algebra,
Vol. 655,
Issue. ,
p.
517.
Çınarcı, Burcu
and
Keller, Thomas
2024.
A new lower bound for the number of conjugacy classes.
Proceedings of the American Mathematical Society,
Keller, Thomas Michael
and
Yang, Yong
2025.
Bounding the number of p'-degree characters from below.
Forum Mathematicum,


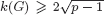 with equality if and only if if
with equality if and only if if 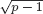 is an integer,
is an integer,  and
and 