Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T16:56:09.110Z Has data issue: false hasContentIssue false
  • English
  • Français

Hecke C*-algebras and semi-direct products

Part of: Representation theory of groups Selfadjoint operator algebras

Published online by Cambridge University Press:  02 February 2009

S. Kaliszewski ,
Magnus B. Landstad  and
John Quigg
S. Kaliszewski
Affiliation:
Department of Mathematics and Statistics, Arizona State University, Tempe, AZ 85287, USA (quigg@asu.edu; kaliszewski@asu.edu)
Magnus B. Landstad
Affiliation:
Department of Mathematical Sciences, Norwegian University of Science and Technology, 7491 Trondheim, Norway (magnusla@math.ntnu.no)
John Quigg
Affiliation:
Department of Mathematics and Statistics, Arizona State University, Tempe, AZ 85287, USA (quigg@asu.edu; kaliszewski@asu.edu)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We analyse Hecke pairs (G,H) and the associated Hecke algebra 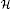when G is a semi-direct product N ⋊ Q and H = M ⋊ R for subgroups M ⊂ N and R ⊂ Q with M normal in N. Our main result shows that, when (G,H) coincides with its Schlichting completion and R is normal in Q, the closure of 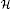in C*(G) is Morita–Rieffel equivalent to a crossed product I⋊βQ/R, where I is a certain ideal in the fixed-point algebra C*(N)R. Several concrete examples are given illustrating and applying our techniques, including some involving subgroups of GL(2,K) acting on K2, where K = ℚ or K = ℤ[p−1]. In particular we look at the ax + b group of a quadratic extension of K.

Keywords

Hecke algebragroup C*-algebraMorita equivalencesemi-direct product

MSC classification

Secondary: 46L55: Noncommutative dynamical systems 20C08: Hecke algebras and their representations
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 52 , Issue 1 , February 2009 , pp. 127 - 153
Copyright
Copyright © Edinburgh Mathematical Society 2009