Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T05:58:33.426Z Has data issue: false hasContentIssue false
  • English
  • Français

Hecke C*-Algebras, Schlichting Completions and Morita Equivalence

Published online by Cambridge University Press:  12 December 2008

S. Kaliszewski ,
Magnus B. Landstad  and
John Quigg
S. Kaliszewski
Affiliation:
Department of Mathematics and Statistics, Arizona State University, Tempe, AZ 85287, USA (kaliszewski@asu.edu; quigg@math.asu.edu)
Magnus B. Landstad
Affiliation:
Department of Mathematical Sciences, Norwegian University of Science and Technology, 7491 Trondheim, Norway (magnusla@math.ntnu.no)
John Quigg
Affiliation:
Department of Mathematics and Statistics, Arizona State University, Tempe, AZ 85287, USA (kaliszewski@asu.edu; quigg@math.asu.edu)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

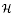The Hecke algebra of a Hecke pair (G, H) is studied using the Schlichting completion (Ḡ, 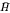), which is a Hecke pair whose Hecke algebra is isomorphic to 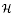and which is topologized so that 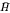is a compact open subgroup of Ḡ. In particular, the representation theory and C*-completions of 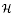are addressed in terms of the projection 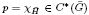using both Fell's and Rieffel's imprimitivity theorems and the identity 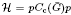. An extended analysis of the case where H is contained in a normal subgroup of G (and in particular the case where G is a semi-direct product) is carried out, and several specific examples are analysed using this approach.

Keywords

Hecke algebratotally disconnected groupgroup C*-algebraMorita equivalence
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 51 , Issue 3 , October 2008 , pp. 657 - 695
Copyright
Copyright © Edinburgh Mathematical Society 2008