Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-10T13:07:31.939Z Has data issue: false hasContentIssue false
  • English
  • Français

Invariance of KMS states on graph C*-algebras under classical and quantum symmetry

Part of: Selfadjoint operator algebras Graph theory

Published online by Cambridge University Press:  20 September 2021

Soumalya Joardar  and
Arnab Mandal
Soumalya Joardar
Affiliation:
Department of Mathematics and Statistics, IISER Kolkata, Mohanpur, West Bengal741246, India (soumalya.j@gmail.com)
Arnab Mandal
Affiliation:
Presidency University, College Street, Kolkata, West Bengal700073, India (arnabmaths@gmail.com)
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the invariance of KMS states on graph $C^{\ast }$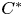-algebras coming from strongly connected and circulant graphs under the classical and quantum symmetry of the graphs. We show that the unique KMS state for strongly connected graphs is invariant under the quantum automorphism group of the graph. For circulant graphs, it is shown that the action of classical and quantum automorphism groups preserves only one of the KMS states occurring at the critical inverse temperature. We also give an example of a graph $C^{\ast }$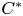-algebra having more than one KMS state such that all of them are invariant under the action of classical automorphism group of the graph, but there is a unique KMS state which is invariant under the action of quantum automorphism group of the graph.

Keywords

KMS statesGraph C*-algebraquantum automorphism group

MSC classification

Primary: 05C50: Graphs and linear algebra (matrices, eigenvalues, etc.)
Secondary: 46L30: States 46L89: Other “noncommutative” mathematics based on $C^*$-algebra theory
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 64 , Issue 4 , November 2021 , pp. 762 - 778
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Atserias, A., Mancinska, L., Roberson, D. E., Samal, R., Severini, S. and Varvitsiotis, A., Quantum and non-signalling graph isomorphisms, J. Comb. Theory, Ser. B 136 (2019), 289–328.CrossRefGoogle Scholar
Banica, T., Quantum automorphism groups of homogeneous graphs, J. Funct. Anal. 224 (2005), 243–280.CrossRefGoogle Scholar
Bichon, J., Quantum automorphism groups of finite graphs, Proc. Am. Math. Soc. 131(3) (2003), 665–673.CrossRefGoogle Scholar
Cuntz, J. and Krieger, W., A class of $C^{\ast }$-algebras and topological Markov chains, Invent. Math. 56 (1980), 251–268.CrossRefGoogle Scholar
Fulton, M., The quantum automorphism group and undirected trees. Ph.D. Thesis, Virginia, 2006.Google Scholar
Huef, A., Laca, M., Raeburn, I. and Sims, A., KMS states on the $C^{\ast }$-algebras of finite graphs, J. Math. Anal. Appl. 405(2) (2013), 388–399.10.1016/j.jmaa.2013.03.055CrossRefGoogle Scholar
Joardar, S. and Mandal, A., Quantum symmetry of graph $C^{\ast }$-algebras associated with connected graphs, Infin. Dimens. Anal., Quantum Probab. Relat. Top. 21 (2018).CrossRefGoogle Scholar
Joardar, S. and Mandal, A., Quantum symmetry of graph $C^{\ast }$-algebras at critical inverse temperature, Stud. Math. 256(1) (2021).10.4064/sm190102-30-9CrossRefGoogle Scholar
Kajiwara, T and Watatani, Y., KMS states on finite graph $C^{\ast }$-algebras, Kyushu J. Math. 67(1) (2013), 83–104.CrossRefGoogle Scholar
Kra, I. and Santiago, S. R., On circulant matrices, web.mit.edu/18.06/www/spring17/Circulant-Matrices.pdf.Google Scholar
Lupini, M., Mancinska, L. and Roberson, D. E., Non local games and quantum permutation groups, to appear in J. Funct. Anal.Google Scholar
Maes, A. and Van Daele, A., Notes on compact quantum groups, Nieuw Arch. Wisk (4) 16(12) (1998), 73–112.Google Scholar
Pask, D. and Rennie, A., The noncommutative geometry of graph $C^{\ast }$-algebras I: Index theorem, J. Funct. Anal. 233 (2006), 92–134.10.1016/j.jfa.2005.07.009CrossRefGoogle Scholar
Schmidt, S. and Weber, M., Quantum symmetry of graph $C^{\ast }$-algberas, Can. Math. Bull. 61(4) (2017).Google Scholar
Wang, S., Quantum symmetry groups of finite spaces, Comm. Math. Phys. 195 (1998), 195–211.10.1007/s002200050385CrossRefGoogle Scholar
Woronowicz, S. L., Compact matrix pseudogroups, Comm. Math. Phys. 111 (1987), 613–665.10.1007/BF01219077CrossRefGoogle Scholar
Zeman, P., Automorphism groups of geometrically presented graphs. Bachelor's thesis, Computer Science Institute, Prague, 2014.Google Scholar