Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-01-26T07:10:07.313Z Has data issue: false hasContentIssue false
  • English
  • Français

Irreducible factors of a polynomial

Part of: Topological fields Algebraic number theory: global fields General field theory

Published online by Cambridge University Press:  24 January 2025

Sneha Mavi Open the ORCID record for Sneha Mavi [Opens in a new window]  and
Anuj Bishnoi Open the ORCID record for Anuj Bishnoi [Opens in a new window]
Sneha Mavi
Affiliation:
Department of Mathematics, University of Delhi, Delhi-110007, India
Anuj Bishnoi*
Affiliation:
Department of Mathematics, University of Delhi, Delhi-110007, India
*
*Corresponding author: Anuj Bishnoi, email: abishnoi@maths.du.ac.in
Get access Rights & Permissions [Opens in a new window]

Abstract

Let (K, v) be a valued field and 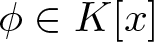$\phi\in K[x]$ be any key polynomial for a residue-transcendental extension w of v to K(x). In this article, using the ϕ-Newton polygon of a polynomial 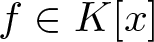$f\in K[x]$ (with respect to w), we give a lower bound for the degree of an irreducible factor of f. This generalizes the result given in Jakhar and Srinivas (On the irreducible factors of a polynomial II, J. Algebra 556 (2020), 649–655).

Keywords

irreducibilitykey polynomialsNewton polygonsvalued fields

MSC classification

Primary: 11R09: Polynomials (irreducibility, etc.)
Secondary: 12E05: Polynomials (irreducibility, etc.) 12J10: Valued fields
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , First View , pp. 1 - 10
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alberich-Carraminãna, M., Guàrdia, J., Nart, E., Poteaux, A., Roé, J. and Weimann, M., Polynomial factorization over Henselian fields, Found. Comput. Math. (2024). doi:10.1007/s10208-024-09646-xCrossRefGoogle Scholar
Alexandru, V., Popescu, N. and Zaharescu, A., A theorem of characterization of residual transcendental extensions of a valuation, J. Math. Kyoto Univ. 28(4) (1988), 579–592.Google Scholar
Engler, A. J. and Prestel, A., Valued Fields (Springer-Verlag, Berlin, 2005).Google Scholar
Guàrdia, J., Montes, J. and Nart, E., Newton polygons of higher order in algebraic number theory, Trans. Amer. Math. Soc. 364(1) (2012), 361–416.CrossRefGoogle Scholar
Jakhar, A.. On the irreducible factors of a polynomial, Proc. Am. Math. Soc. 148(4) (2020), 1429–1437. https://www.ams.org/journals/proc/2020-148-04/home.html?active=allissuesCrossRefGoogle Scholar
Jakhar, A., On the factors of a polynomial, Bull. Lond. Math. Soc. 52(1) (2020), 158–160.CrossRefGoogle Scholar
Jakhar, A., Khanduja, S. K. and Sangwan, N., On factorization of polynomials in Henselian valued fields, Comm. Algebra 46(7) (2018), 3205–3221.CrossRefGoogle Scholar
Jakhar, A. and Srinivas, K., On the irreducible factors of a polynomial II, J. Algebra 556 (2020), 649–655.CrossRefGoogle Scholar
Jakhar, A. and Srinivas, K.. On the degrees of irreducible factors of a polynomial, Proc. Am. Math. Soc. 150(5) (2022), 1949–1953. https://www.ams.org/journals/proc/2022-150-05/home.html?active=allissuesGoogle Scholar
Khanduja, S. K. and Kumar, M., Prolongations of valuations to finite extensions, Manuscr. Math. 131(3-4) (2010), 323–334.CrossRefGoogle Scholar
MacLane, S., A construction for absolute values in polynomial rings, Trans. Amer. Math. Soc. 40(3) (1936), 363–395.CrossRefGoogle Scholar
Nart, E., MacLane-Vaquié chains of valuations on a polynomial ring, Pac. J. Math. 311(1) (2021), 165–195.CrossRefGoogle Scholar
Popescu, L. and Popescu, N., On the residual transcendental extensions of a valuation. Key polynomials and augmented valuation, Tsukuba J. Math. 15(1) (1991), 57–78.CrossRefGoogle Scholar
Vaquié, M., Extension d’une valuation, Trans. Amer. Math. Soc. 359(7) (2007), 3439–3481.CrossRefGoogle Scholar