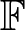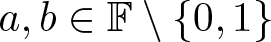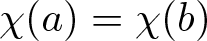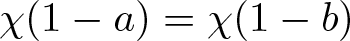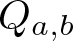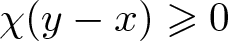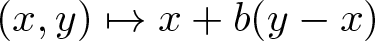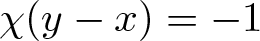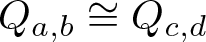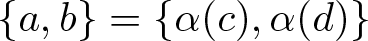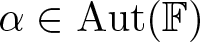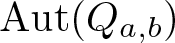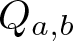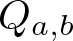1. Main results
Throughout, ![]() $\mathbb F$ will be a finite field of odd order. A quasigroup Q is a set with a binary operation, say ·, such that the equations
$\mathbb F$ will be a finite field of odd order. A quasigroup Q is a set with a binary operation, say ·, such that the equations ![]() $x\cdot a = b$ and
$x\cdot a = b$ and ![]() $a\cdot y=b$ have unique solutions for all
$a\cdot y=b$ have unique solutions for all ![]() $a,b\in Q$. Let
$a,b\in Q$. Let ![]() $\chi:\mathbb F\to \{-1,0,1\}$ be the extended quadratic character, which satisfies
$\chi:\mathbb F\to \{-1,0,1\}$ be the extended quadratic character, which satisfies ![]() $\chi(0)=0$ and sends non-zero squares and non-squares to +1 and −1, respectively. For any
$\chi(0)=0$ and sends non-zero squares and non-squares to +1 and −1, respectively. For any ![]() $a,b \in \mathbb F$, there exists an operation
$a,b \in \mathbb F$, there exists an operation ![]() $*$ on
$*$ on ![]() $\mathbb F$ such that
$\mathbb F$ such that
 \begin{equation}
x*y = \begin{cases} x+a(y-x) & \text{if} \ \chi(y-x) \geqslant 0, \\
x+b(y-x) &\text{if} \ \chi(y-x) = -1. \end{cases}
\end{equation}
\begin{equation}
x*y = \begin{cases} x+a(y-x) & \text{if} \ \chi(y-x) \geqslant 0, \\
x+b(y-x) &\text{if} \ \chi(y-x) = -1. \end{cases}
\end{equation}This operation yields a quasigroup (see e.g. [Reference Evans8]) if and only if
If Condition (1.2) holds, then the quasigroup given by Condition (1.1) will be denoted by ![]() $Q_{a,b}$. A finite quasigroup isomorphic to a quasigroup
$Q_{a,b}$. A finite quasigroup isomorphic to a quasigroup ![]() $Q_{a,b}$ is said to be quadratic. Note that quadratic quasigroups are idempotent, i.e., they satisfy the law xx = x.
$Q_{a,b}$ is said to be quadratic. Note that quadratic quasigroups are idempotent, i.e., they satisfy the law xx = x.
Quadratic quasigroups have many applications, including the construction of mutually orthogonal Latin squares [Reference Evans7, Reference Evans8], atomic Latin squares [Reference Wanless14], Falconer varieties [Reference Allsop and Wanless1], perfect 1-factorizations of graphs [Reference Allsop and Wanless1, Reference Gill and Wanless9, Reference Wanless14] and maximally non-associative quasigroups [Reference Drápal and Wanless5]. A question raised by [Reference Drápal and Wanless5] was to understand when two quadratic quasigroups are isomorphic. Our first main result answers this question:
Theorem 1.1. Let ![]() $Q_{a,b}$ and
$Q_{a,b}$ and ![]() $Q_{c,d}$ be quadratic quasigroups over
$Q_{c,d}$ be quadratic quasigroups over ![]() $\mathbb F$. Then
$\mathbb F$. Then ![]() $Q_{a,b}\cong Q_{c,d}$ if and only if there exists
$Q_{a,b}\cong Q_{c,d}$ if and only if there exists ![]() $\alpha \in \operatorname{Aut}(\mathbb F)$ such that
$\alpha \in \operatorname{Aut}(\mathbb F)$ such that ![]() $\{a,b\} = \{\alpha(c),\alpha(d)\}$.
$\{a,b\} = \{\alpha(c),\alpha(d)\}$.
In [Reference Wanless14], it was noted that quadratic quasigroups have rich automorphism groups. Our second major goal is to fully understand these groups. We start by defining the following groups:
•
 $\mathrm A \Gamma \mathrm L_1(\mathbb F)$ is the group of all affine semilinear mappings
$\mathrm A \Gamma \mathrm L_1(\mathbb F)$ is the group of all affine semilinear mappings  $x \mapsto \lambda \alpha(x) + \mu$, where
$x \mapsto \lambda \alpha(x) + \mu$, where  $\lambda\in\mathbb F^*$,
$\lambda\in\mathbb F^*$,  $\mu \in \mathbb F$ and
$\mu \in \mathbb F$ and  $\alpha \in \operatorname{Aut}(\mathbb F)$.
$\alpha \in \operatorname{Aut}(\mathbb F)$.•
 $\mathrm A \Gamma \mathrm L_1(\mathbb F\,{\mid}\, \mathbb K)$ is the subgroup of
$\mathrm A \Gamma \mathrm L_1(\mathbb F\,{\mid}\, \mathbb K)$ is the subgroup of  $\mathrm A \Gamma \mathrm L_1(\mathbb F)$ in which the automorphism
$\mathrm A \Gamma \mathrm L_1(\mathbb F)$ in which the automorphism  $\alpha\in \operatorname{Aut}(\mathbb F)$ fixes every element of a subfield
$\alpha\in \operatorname{Aut}(\mathbb F)$ fixes every element of a subfield  $\mathbb K$ of
$\mathbb K$ of  $\mathbb F$ (in other words,
$\mathbb F$ (in other words,  $\alpha \in \operatorname{Gal}(\mathbb F\,{\mid}\, \mathbb K)$).
$\alpha \in \operatorname{Gal}(\mathbb F\,{\mid}\, \mathbb K)$).•
 $\mathrm A \Gamma^2 \mathrm L_1(\mathbb F)$ is the subgroup of
$\mathrm A \Gamma^2 \mathrm L_1(\mathbb F)$ is the subgroup of  $\mathrm A \Gamma \mathrm L_1(\mathbb F)$ consisting of all maps
$\mathrm A \Gamma \mathrm L_1(\mathbb F)$ consisting of all maps  $x \mapsto \lambda \alpha(x) + \mu$ such that
$x \mapsto \lambda \alpha(x) + \mu$ such that  $\chi(\lambda) = 1$.
$\chi(\lambda) = 1$.•
 $\mathrm A \Gamma^2 \mathrm L_1(\mathbb F\,{\mid}\, \mathbb K) = \mathrm A \Gamma^2 \mathrm L_1(\mathbb F)\cap \mathrm A \Gamma \mathrm L_1(\mathbb F\,{\mid}\, \mathbb K)$.
$\mathrm A \Gamma^2 \mathrm L_1(\mathbb F\,{\mid}\, \mathbb K) = \mathrm A \Gamma^2 \mathrm L_1(\mathbb F)\cap \mathrm A \Gamma \mathrm L_1(\mathbb F\,{\mid}\, \mathbb K)$.
The index of ![]() $\mathrm A \Gamma^2 \mathrm L_1(\mathbb F\,{\mid}\, \mathbb K)$ in
$\mathrm A \Gamma^2 \mathrm L_1(\mathbb F\,{\mid}\, \mathbb K)$ in ![]() $\mathrm A \Gamma \mathrm L_1(\mathbb F\,{\mid}\, \mathbb K)$ is equal to two. If there exists a subfield
$\mathrm A \Gamma \mathrm L_1(\mathbb F\,{\mid}\, \mathbb K)$ is equal to two. If there exists a subfield ![]() $\mathbb L$ such that
$\mathbb L$ such that ![]() $[\mathbb K:\mathbb L]=2$, then it is possible to construct another group of affine semilinear mappings in which
$[\mathbb K:\mathbb L]=2$, then it is possible to construct another group of affine semilinear mappings in which ![]() $\mathrm A \Gamma^2 \mathrm L_1(\mathbb F\,{\mid}\, \mathbb K)$ forms a subgroup of index two. This group is said to be a twist of
$\mathrm A \Gamma^2 \mathrm L_1(\mathbb F\,{\mid}\, \mathbb K)$ forms a subgroup of index two. This group is said to be a twist of ![]() $\mathrm A \Gamma \mathrm L_1(\mathbb F{\mid} \mathbb K)$. It is denoted by
$\mathrm A \Gamma \mathrm L_1(\mathbb F{\mid} \mathbb K)$. It is denoted by ![]() $\mathrm A \Gamma \mathrm L^{\mathrm{tw}}_1(\mathbb F\,{\mid}\, \mathbb K)$ and consists of
$\mathrm A \Gamma \mathrm L^{\mathrm{tw}}_1(\mathbb F\,{\mid}\, \mathbb K)$ and consists of ![]() $\mathrm A \Gamma^2 \mathrm L_1(\mathbb F{\mid} \mathbb K)$ and all mappings
$\mathrm A \Gamma^2 \mathrm L_1(\mathbb F{\mid} \mathbb K)$ and all mappings
Theorem 1.2. Let ![]() $Q=Q_{a,b}$ be a quadratic quasigroup over
$Q=Q_{a,b}$ be a quadratic quasigroup over ![]() $\mathbb F$. Denote by
$\mathbb F$. Denote by ![]() $\mathbb K$ the least subfield of
$\mathbb K$ the least subfield of ![]() $\mathbb F$ that contains
$\mathbb F$ that contains ![]() $\{a,b\}$. The automorphism group of Q is equal to
$\{a,b\}$. The automorphism group of Q is equal to ![]() $\mathrm A \Gamma^2 \mathrm L_1(\mathbb F{\mid} \mathbb K)$ up to these exceptions:
$\mathrm A \Gamma^2 \mathrm L_1(\mathbb F{\mid} \mathbb K)$ up to these exceptions:
(i) If a = b, then
 $\operatorname{Aut}(Q) \cong \operatorname{AGL}_k(\mathbb K)$, where
$\operatorname{Aut}(Q) \cong \operatorname{AGL}_k(\mathbb K)$, where  $k=[\mathbb F:\mathbb K]$. The automorphisms of Q are all mappings
$k=[\mathbb F:\mathbb K]$. The automorphisms of Q are all mappings  $x\mapsto \sigma(x)+\mu$, where
$x\mapsto \sigma(x)+\mu$, where  $\mu \in \mathbb F$ and
$\mu \in \mathbb F$ and  $\sigma\colon\mathbb F \to \mathbb F$ is a
$\sigma\colon\mathbb F \to \mathbb F$ is a  $\mathbb K$-linear bijection.
$\mathbb K$-linear bijection.(ii) If there is an integer γ such that
 $b=a^\gamma$ and
$b=a^\gamma$ and  $\gamma^2 = |\mathbb K|$, then
$\gamma^2 = |\mathbb K|$, then  $\operatorname{Aut}(Q) = \mathrm A \Gamma \mathrm L^{\mathrm{tw}}_1(\mathbb F{\mid} \mathbb K)$.
$\operatorname{Aut}(Q) = \mathrm A \Gamma \mathrm L^{\mathrm{tw}}_1(\mathbb F{\mid} \mathbb K)$.(iii) If
 $|\mathbb F|=7$ and
$|\mathbb F|=7$ and  $\{a,b\} = \{3,5\}$, then
$\{a,b\} = \{3,5\}$, then  $\operatorname{Aut}(Q) \cong \operatorname{PSL}_2(7)$.
$\operatorname{Aut}(Q) \cong \operatorname{PSL}_2(7)$.
The proof of Theorem 1.2 leads us to examine several varieties of quasigroup, and it becomes important to understand which quadratic quasigroups those varieties contain. This leads to our third main result:
Theorem 1.3. Let ![]() $Q=Q_{a,b}$ be a quadratic quasigroup over
$Q=Q_{a,b}$ be a quadratic quasigroup over ![]() $\mathbb F$. Then
$\mathbb F$. Then
(i) Q is entropic (i.e. fulfils the law
 $xy\cdot uv = xu\cdot yv$) if and only if a = b;
$xy\cdot uv = xu\cdot yv$) if and only if a = b;(ii) Q is left distributive (i.e. fulfils the law
 $x\cdot yz = xy \cdot xz$) if and only if a = b;
$x\cdot yz = xy \cdot xz$) if and only if a = b;(iii) Q is right distributive (i.e. fulfils the law
 $xy \cdot z = xz\cdot yz$) if and only if a = b;
$xy \cdot z = xz\cdot yz$) if and only if a = b;(iv) Q is commutative if and only if
 $a+b = 1$ and either
$a+b = 1$ and either  $|\mathbb F|\equiv3\bmod4$ or a = b.
$|\mathbb F|\equiv3\bmod4$ or a = b.(v) Q is flexible (i.e. fulfils the law
 $x\cdot yx = xy \cdot x$) if and only if a = b or
$x\cdot yx = xy \cdot x$) if and only if a = b or  $\chi(a) = \chi(1-a) = 1$ or both
$\chi(a) = \chi(1-a) = 1$ or both  $a+b =1$ and
$a+b =1$ and  $|\mathbb F|\equiv3\bmod4$;
$|\mathbb F|\equiv3\bmod4$;(vi) Q is semisymmetric (i.e. fulfils the law
 $xy \cdot x=y$) if and only if
$xy \cdot x=y$) if and only if  $a^2-a+1=0$ and either a = b or
$a^2-a+1=0$ and either a = b or  $a+b=1$.
$a+b=1$.(vii) Q is a Steiner quasigroup (i.e. idempotent, commutative and semisymmetric) if and only if either
 $\operatorname{char}(\mathbb F)=3$ and
$\operatorname{char}(\mathbb F)=3$ and  $a=b=-1$, or
$a=b=-1$, or  $\operatorname{char}(\mathbb F) \gt 3$,
$\operatorname{char}(\mathbb F) \gt 3$,  $a+b=ab=1$ and
$a+b=ab=1$ and  $\chi(a)=\chi(-1)=-1$. In the latter case,
$\chi(a)=\chi(-1)=-1$. In the latter case,  $a\ne b$.
$a\ne b$.(viii) Q is isotopic to a group if and only if a = b.
Another outcome from our work is a precise characterization of all minimal subquasigroups of quadratic quasigroups ![]() $Q_{a,b}$. See Theorems 5.4 and 5.5.
$Q_{a,b}$. See Theorems 5.4 and 5.5.
Regarding Theorem 1.3(i), we note that entropic quasigroups are also sometimes called medial.
Regarding Theorem 1.3(vii), we make the following remarks. If ![]() $\operatorname{char}(\mathbb F) = 3$, then
$\operatorname{char}(\mathbb F) = 3$, then ![]() $Q_{a,b}$ is Steiner if and only if
$Q_{a,b}$ is Steiner if and only if ![]() $a=b=-1$. Steiner quadratic quasigroups in characteristic 3 thus coincide with affine STSs. If
$a=b=-1$. Steiner quadratic quasigroups in characteristic 3 thus coincide with affine STSs. If ![]() $\operatorname{char}(\mathbb F) \gt 3$, then
$\operatorname{char}(\mathbb F) \gt 3$, then ![]() $Q_{a,b}$ is a Steiner quasigroup if and only if
$Q_{a,b}$ is a Steiner quasigroup if and only if ![]() $a+b=1=ab$ and
$a+b=1=ab$ and ![]() $\chi(a)=\chi(b)=\chi(-1) =-1$. An easy number theoretical argument shows that this happens if and only if
$\chi(a)=\chi(b)=\chi(-1) =-1$. An easy number theoretical argument shows that this happens if and only if ![]() $|\mathbb F| = p^k$ for a prime
$|\mathbb F| = p^k$ for a prime ![]() $p\equiv 7 \bmod 12$ and odd
$p\equiv 7 \bmod 12$ and odd ![]() $k\geqslant 1$, and a and b are distinct primitive sixth roots of unity. Blocks of the STS are the sets
$k\geqslant 1$, and a and b are distinct primitive sixth roots of unity. Blocks of the STS are the sets ![]() $\{u,v,av+bu\}$, where
$\{u,v,av+bu\}$, where ![]() $\chi(v-u) = 1$. These STSs are known as Netto systems, and we refer to the corresponding quasigroups as Netto quasigroups. Robinson [Reference Robinson11] proved that their automorphism group is equal to
$\chi(v-u) = 1$. These STSs are known as Netto systems, and we refer to the corresponding quasigroups as Netto quasigroups. Robinson [Reference Robinson11] proved that their automorphism group is equal to ![]() $\mathrm A \Gamma^2 \mathrm L_1(\mathbb F)$, with the exception of order 7, which yields the Fano plane – and thus also Theorem 1.2(iii).
$\mathrm A \Gamma^2 \mathrm L_1(\mathbb F)$, with the exception of order 7, which yields the Fano plane – and thus also Theorem 1.2(iii).
Say that a quadratic quasigroup ![]() $Q = Q_{a,b}$ is twisted if
$Q = Q_{a,b}$ is twisted if ![]() $b = a^\gamma$, where γ 2 is the order of the least subfield of
$b = a^\gamma$, where γ 2 is the order of the least subfield of ![]() $\mathbb F$ containing the element a. The exceptional cases of Theorem 1.2 may thus be labelled entropic, twisted and Fano. It is immediately clear that these are the only cases in which
$\mathbb F$ containing the element a. The exceptional cases of Theorem 1.2 may thus be labelled entropic, twisted and Fano. It is immediately clear that these are the only cases in which ![]() $\operatorname{Aut}(Q)$ is 2-transitive.
$\operatorname{Aut}(Q)$ is 2-transitive.
Twisted quadratic quasigroups are closely related to quasigroups constructed from quadratic nearfields. The axioms of a (left) nearfield ![]() $(N,+,\circ,0,1)$ stipulate that
$(N,+,\circ,0,1)$ stipulate that ![]() $(N,+,0)$ is an abelian group,
$(N,+,0)$ is an abelian group, ![]() $(N\setminus\{0\},\circ,1)$ is a group,
$(N\setminus\{0\},\circ,1)$ is a group, ![]() $0\circ x = 0 = x\circ 0$ for all
$0\circ x = 0 = x\circ 0$ for all ![]() $x\in N$ and
$x\in N$ and ![]() $x\circ(y+z) = x\circ y + x \circ z$, for all
$x\circ(y+z) = x\circ y + x \circ z$, for all ![]() $x,y,z\in N$. A quadratic nearfield is defined over a field
$x,y,z\in N$. A quadratic nearfield is defined over a field ![]() $\mathbb F_{q^2}$, where q is a power of an odd prime, by
$\mathbb F_{q^2}$, where q is a power of an odd prime, by
 \begin{equation}
x\circ y = \begin{cases} xy& \text{if} \ \chi(x) \geqslant 0; \\
xy^q & \text{if} \ \chi(x) = -1.
\end{cases}
\end{equation}
\begin{equation}
x\circ y = \begin{cases} xy& \text{if} \ \chi(x) \geqslant 0; \\
xy^q & \text{if} \ \chi(x) = -1.
\end{cases}
\end{equation} With each element ![]() $c\notin \{0,1\}$ of a nearfield N, there may be associated a quasigroup
$c\notin \{0,1\}$ of a nearfield N, there may be associated a quasigroup ![]() $(N,*_c)$ for which
$(N,*_c)$ for which
Stein [Reference Stein12] showed that each of the mappings ![]() $x\mapsto \lambda \circ x + \mu$, where
$x\mapsto \lambda \circ x + \mu$, where ![]() $\lambda \in N\setminus\{0\}$ and
$\lambda \in N\setminus\{0\}$ and ![]() $\mu\in N$, is an automorphism of
$\mu\in N$, is an automorphism of ![]() $(N,*_c)$. For background on nearfields, see [Reference Wähling13].
$(N,*_c)$. For background on nearfields, see [Reference Wähling13].
The notation  $(\mathbb F_{q^2},*_c)$ will always refer to the quasigroup built by means of Condition (1.4) over the quadratic nearfield that is defined on
$(\mathbb F_{q^2},*_c)$ will always refer to the quasigroup built by means of Condition (1.4) over the quadratic nearfield that is defined on ![]() $\mathbb F_{q^2}$ by Condition (1.3). These quasigroups may also be obtained by means of Condition (1.1) as quadratic quasigroups:
$\mathbb F_{q^2}$ by Condition (1.3). These quasigroups may also be obtained by means of Condition (1.1) as quadratic quasigroups:
Proposition 1.4. Suppose that ![]() $|\mathbb F| = q^2$ and that
$|\mathbb F| = q^2$ and that ![]() $a\in \mathbb F\setminus\{0,1\}$. Then
$a\in \mathbb F\setminus\{0,1\}$. Then  $Q_{a,a^q} = (\mathbb F_{q^2},*_a)$ and
$Q_{a,a^q} = (\mathbb F_{q^2},*_a)$ and  $Q_{a^q,a} =
(\mathbb F_{q^2},*_{a^q})$. The mapping
$Q_{a^q,a} =
(\mathbb F_{q^2},*_{a^q})$. The mapping ![]() $x\mapsto x^q$ yields an isomorphism
$x\mapsto x^q$ yields an isomorphism  $(\mathbb F_{q^2},*_a)\cong (\mathbb F_{q^2},*_{a^q})$.
$(\mathbb F_{q^2},*_a)\cong (\mathbb F_{q^2},*_{a^q})$.
Proof. We use ![]() $*$ to denote the operation of
$*$ to denote the operation of ![]() $Q_{a,a^q}$. If y − x is a square, then
$Q_{a,a^q}$. If y − x is a square, then ![]() $x*y = x+(y-x)a = x+ (y-x)\circ a= x*_a y$. If y − x is a non-square, then
$x*y = x+(y-x)a = x+ (y-x)\circ a= x*_a y$. If y − x is a non-square, then ![]() $x*y = x+(y-x)a^q = x+ (y-x)\circ a = x*_a y$, for all
$x*y = x+(y-x)a^q = x+ (y-x)\circ a = x*_a y$, for all ![]() $x,y \in \mathbb F$. It follows that
$x,y \in \mathbb F$. It follows that  $Q_{a,a^q} = (\mathbb F_{q^2},*_a)$, and then by substituting aq for a, we find that
$Q_{a,a^q} = (\mathbb F_{q^2},*_a)$, and then by substituting aq for a, we find that  $Q_{a^q,a} = (\mathbb F_{q^2},*_{a^q})$. The fact that
$Q_{a^q,a} = (\mathbb F_{q^2},*_{a^q})$. The fact that ![]() $x\mapsto x^q$ is an isomorphism
$x\mapsto x^q$ is an isomorphism ![]() $Q_{a,a^q}\cong Q_{a^q,a}$ was shown in [Reference Wanless14] (and also follows from Proposition 2.1).
$Q_{a,a^q}\cong Q_{a^q,a}$ was shown in [Reference Wanless14] (and also follows from Proposition 2.1).
Let us briefly outline the content of the following sections. Section 2 consists of straightforward arguments that establish Theorem 1.3. To avoid repeating the same condition, let us assume in the rest of this overview that ![]() $Q = Q_{a,b}$ is a quadratic quasigroup defined on the field
$Q = Q_{a,b}$ is a quadratic quasigroup defined on the field ![]() $\mathbb F = \mathbb F_q$ by means of Condition (1.1) such that
$\mathbb F = \mathbb F_q$ by means of Condition (1.1) such that ![]() $a\ne b$ and such that Q is not a Steiner quasigroup.
$a\ne b$ and such that Q is not a Steiner quasigroup.
The main achievement of Section 3 is Proposition 3.4, which shows that every subquasigroup of Q containing 0 is closed under the addition of ![]() $\mathbb F$. Section 4 starts by investigating the situation when there exists an additive
$\mathbb F$. Section 4 starts by investigating the situation when there exists an additive ![]() $\varphi \in \operatorname{Aut}(Q)$ such that
$\varphi \in \operatorname{Aut}(Q)$ such that ![]() $\varphi(1)$ is a non-square in
$\varphi(1)$ is a non-square in ![]() $\mathbb F$. Several technical results are needed to obtain Proposition 4.5 by which the latter condition implies that Q is twisted. That suffices to prove Theorem 1.2 for the case of Q being 2-generated. That is done in Theorem 4.7. The structure of
$\mathbb F$. Several technical results are needed to obtain Proposition 4.5 by which the latter condition implies that Q is twisted. That suffices to prove Theorem 1.2 for the case of Q being 2-generated. That is done in Theorem 4.7. The structure of ![]() $\operatorname{Aut}(Q)$ is then used to establish, in Theorem 4.8, the validity of Theorem 1.1 when Q is 2-generated.
$\operatorname{Aut}(Q)$ is then used to establish, in Theorem 4.8, the validity of Theorem 1.1 when Q is 2-generated.
Assume now that Q is not 2-generated. Call a subquasigroup minimal if it consists of more than one element and has no proper subquasigroup with more than one element. Section 5 is devoted to the description of minimal subquasigroups of Q and of 2-generated subquasigroups of Q. This is achieved in Theorems 5.4 and 5.5. It turns out that such subquasigroups may be used to get a structure of affine lines belonging to a subfield of ![]() $\mathbb F$. Since an automorphism of Q has to respect such a structure, it has to be induced by semilinear mappings (Proposition 5.8). It turns out that such a mapping has to be linear in many cases (Proposition 6.2) and that allows us, by an application of a theorem of Carlitz, to confirm the structure of
$\mathbb F$. Since an automorphism of Q has to respect such a structure, it has to be induced by semilinear mappings (Proposition 5.8). It turns out that such a mapping has to be linear in many cases (Proposition 6.2) and that allows us, by an application of a theorem of Carlitz, to confirm the structure of ![]() $\operatorname{Aut}(Q)$ as described in Theorem 1.2. Knowledge of
$\operatorname{Aut}(Q)$ as described in Theorem 1.2. Knowledge of ![]() $\operatorname{Aut}(Q)$ is then used to prove Theorem 1.1 in its general form.
$\operatorname{Aut}(Q)$ is then used to prove Theorem 1.1 in its general form.
2. Varieties of quadratic quasigroups
This section is primarily aimed at proving Theorem 1.3. The proof is split between Lemmas 2.3–2.8 below. Let ![]() $Q = Q_{a,b}$ be a quadratic quasigroup over
$Q = Q_{a,b}$ be a quadratic quasigroup over ![]() $\mathbb F$. We wish to give easily checkable conditions on
$\mathbb F$. We wish to give easily checkable conditions on ![]() $a,b$ under which Q is entropic, left or right distributive, commutative, flexible, semisymmetric or totally symmetric. Note that totally symmetric is a term describing the combination of commutative and semisymmetric. Steiner quasigroups are precisely those that are idempotent and totally symmetric.
$a,b$ under which Q is entropic, left or right distributive, commutative, flexible, semisymmetric or totally symmetric. Note that totally symmetric is a term describing the combination of commutative and semisymmetric. Steiner quasigroups are precisely those that are idempotent and totally symmetric.
We start with some basic properties of quadratic quasigroups. If ![]() $(Q,*)$ is a quasigroup, then the opposite and the translate of
$(Q,*)$ is a quasigroup, then the opposite and the translate of ![]() $(Q,*)$ are, respectively, the quasigroups
$(Q,*)$ are, respectively, the quasigroups ![]() $(Q,\circ)$ and
$(Q,\circ)$ and ![]() $(Q,\otimes)$ defined by
$(Q,\otimes)$ defined by ![]() $x*y=z\Leftrightarrow y\circ x=z\Leftrightarrow z\otimes x=y$. The following statement, with the exception of points (vii) and (viii), is immediate from [Reference Wanless14].
$x*y=z\Leftrightarrow y\circ x=z\Leftrightarrow z\otimes x=y$. The following statement, with the exception of points (vii) and (viii), is immediate from [Reference Wanless14].
Proposition 2.1. Let ![]() $Q_{a,b}$ be a quadratic quasigroup over
$Q_{a,b}$ be a quadratic quasigroup over ![]() $\mathbb F$.
$\mathbb F$.
(i)
 $Q_{a,b}$ is idempotent.
$Q_{a,b}$ is idempotent.(ii) For any
 $f\in\mathbb F$, the map
$f\in\mathbb F$, the map  $x\mapsto x+f$ is an automorphism of
$x\mapsto x+f$ is an automorphism of  $Q_{a,b}$.
$Q_{a,b}$.(iii) For any non-zero square
 $c\in\mathbb F$, the map
$c\in\mathbb F$, the map  $x\mapsto cx$ is an automorphism of
$x\mapsto cx$ is an automorphism of  $Q_{a,b}$.
$Q_{a,b}$.(iv)
 $Q_{a,b}$ is isomorphic to
$Q_{a,b}$ is isomorphic to  $Q_{b,a}$ by the map
$Q_{b,a}$ by the map  $x\mapsto\zeta x$, where ζ is any non-square in
$x\mapsto\zeta x$, where ζ is any non-square in  $\mathbb F$.
$\mathbb F$.(v) The opposite quasigroup of
 $Q_{a,b}$ is
$Q_{a,b}$ is  $Q_{1-a,1-b}$ if
$Q_{1-a,1-b}$ if  $|\mathbb F|\equiv1\bmod4$ and
$|\mathbb F|\equiv1\bmod4$ and  $Q_{1-b,1-a}$ if
$Q_{1-b,1-a}$ if  $|\mathbb F|\equiv3\bmod4$.
$|\mathbb F|\equiv3\bmod4$.(vi) The translate of
 $Q_{a,b}$ is
$Q_{a,b}$ is  $Q_{(a-1)/a,(b-1)/b}$ if
$Q_{(a-1)/a,(b-1)/b}$ if  $\chi(a)=\chi(-1)$ and
$\chi(a)=\chi(-1)$ and  $Q_{(b-1)/b,(a-1)/a}$ if
$Q_{(b-1)/b,(a-1)/a}$ if  $\chi(a)\ne\chi(-1)$.
$\chi(a)\ne\chi(-1)$.(vii) If
 $a\ne b$ and ζ is a non-square in
$a\ne b$ and ζ is a non-square in  $\mathbb F$, then
$\mathbb F$, then  $\zeta(x*y)\ne (\zeta x)*(\zeta y)$ for all distinct
$\zeta(x*y)\ne (\zeta x)*(\zeta y)$ for all distinct  $x,y\in \mathbb F$.
$x,y\in \mathbb F$.(viii) If
 $\alpha\in \operatorname{Aut}(\mathbb F)$, then α induces an automorphism between
$\alpha\in \operatorname{Aut}(\mathbb F)$, then α induces an automorphism between  $Q_{a,b}$ and
$Q_{a,b}$ and  $Q_{\alpha(a),\alpha(b)}$.
$Q_{\alpha(a),\alpha(b)}$.
Proof. To prove (vii), consider ![]() $x,y \in \mathbb F$. If
$x,y \in \mathbb F$. If ![]() $\chi(y-x) = 1$, then
$\chi(y-x) = 1$, then ![]() $\zeta(x*y) = \zeta x + a\zeta(y-x)$, while
$\zeta(x*y) = \zeta x + a\zeta(y-x)$, while ![]() $\zeta x * \zeta y = \zeta x + b\zeta(y-x)$. If
$\zeta x * \zeta y = \zeta x + b\zeta(y-x)$. If ![]() $\chi(y-x) = -1$, then
$\chi(y-x) = -1$, then ![]() $\zeta(x*y) = \zeta x + b\zeta(y-x)$, while
$\zeta(x*y) = \zeta x + b\zeta(y-x)$, while ![]() $\zeta x * \zeta y = \zeta x + a\zeta(y-x)$.
$\zeta x * \zeta y = \zeta x + a\zeta(y-x)$.
To prove (viii), note that ![]() $\chi(y-x) = \chi(\alpha(y-x)) =\chi(\alpha(y)-\alpha(x))$ for all
$\chi(y-x) = \chi(\alpha(y-x)) =\chi(\alpha(y)-\alpha(x))$ for all ![]() $x,y \in Q$. Hence,
$x,y \in Q$. Hence, ![]() $x*y = x+a(y-x)$ in
$x*y = x+a(y-x)$ in ![]() $Q_{a,b}$ if and only if
$Q_{a,b}$ if and only if
in ![]() $Q_{\alpha(a),\alpha(b)}$. The argument remains true if a is replaced by b, so
$Q_{\alpha(a),\alpha(b)}$. The argument remains true if a is replaced by b, so ![]() $\alpha(x)*\alpha(y) =\alpha(x*y)$ in all cases.
$\alpha(x)*\alpha(y) =\alpha(x*y)$ in all cases.
Lemma 2.2. Suppose ![]() $\mathbb F$ is a finite field of odd order
$\mathbb F$ is a finite field of odd order ![]() $|\mathbb F| \gt 9$. Then there exist
$|\mathbb F| \gt 9$. Then there exist ![]() $u,v\in\mathbb F$ such that
$u,v\in\mathbb F$ such that ![]() $\chi(u)=\chi(v)=\chi(u+1)=\chi(v+1)=\chi(u-1)=-1$ and
$\chi(u)=\chi(v)=\chi(u+1)=\chi(v+1)=\chi(u-1)=-1$ and ![]() $\chi(v-1)=1$.
$\chi(v-1)=1$.
Proof. The statement is concerned with two special cases of a more general problem that asks if for ![]() $\varepsilon_i\in \{-1,1\}$,
$\varepsilon_i\in \{-1,1\}$, ![]() $-1\leqslant i \leqslant 1$, there exists
$-1\leqslant i \leqslant 1$, there exists ![]() $x \in \mathbb F$ such that
$x \in \mathbb F$ such that ![]() $\chi(x+i) = \varepsilon_i$. A consequence of Weil’s bound (e.g., as stated in [Reference Drápal and Wanless6, Theorem 1.6]) implies that such an x exists if
$\chi(x+i) = \varepsilon_i$. A consequence of Weil’s bound (e.g., as stated in [Reference Drápal and Wanless6, Theorem 1.6]) implies that such an x exists if
where ![]() $q= |\mathbb F|$. This is true for each prime power q > 43. For prime values q = 11, 13, 17, 19, 23, 29, 31, 37, 41 and 43, put u = 7, 6, 6, 13, 20, 11, 12, 14, 12 and 19, respectively. For q = 25, set
$q= |\mathbb F|$. This is true for each prime power q > 43. For prime values q = 11, 13, 17, 19, 23, 29, 31, 37, 41 and 43, put u = 7, 6, 6, 13, 20, 11, 12, 14, 12 and 19, respectively. For q = 25, set ![]() $u = 2\sqrt 2$. In all these cases, set
$u = 2\sqrt 2$. In all these cases, set ![]() $v = u-1$. For q = 27, set u = x and
$v = u-1$. For q = 27, set u = x and ![]() $v=2x^2$ in
$v=2x^2$ in ![]() $\mathbb F_3[x]/(x^3+2x+1)$.
$\mathbb F_3[x]/(x^3+2x+1)$.
Lemma 2.3. Suppose that ![]() $Q=Q_{a,b}$ is a quadratic quasigroup over
$Q=Q_{a,b}$ is a quadratic quasigroup over ![]() $\mathbb F$. Then Q is isotopic to a group if and only if a = b.
$\mathbb F$. Then Q is isotopic to a group if and only if a = b.
Proof. First suppose that a = b, so that ![]() $(Q,*)$ is defined by
$(Q,*)$ is defined by ![]() $x*y=(1-a)x+ay$ for all
$x*y=(1-a)x+ay$ for all ![]() $x,y\in\mathbb F$. So Q is isotopic to the additive group of
$x,y\in\mathbb F$. So Q is isotopic to the additive group of ![]() $\mathbb F$.
$\mathbb F$.
For the remainder of this proof, suppose that ![]() $a\ne b$. We use the well known quadrangle criterion (see e.g. [Reference Evans8]) to show that Q is not isotopic to any group. This criterion states that if Q is isotopic to a group and
$a\ne b$. We use the well known quadrangle criterion (see e.g. [Reference Evans8]) to show that Q is not isotopic to any group. This criterion states that if Q is isotopic to a group and ![]() $r_1,r_2,c_1,c_2,r_1^{\prime},r_2^{\prime},c_1^{\prime},c_2^{\prime}$ are any elements of Q such that
$r_1,r_2,c_1,c_2,r_1^{\prime},r_2^{\prime},c_1^{\prime},c_2^{\prime}$ are any elements of Q such that ![]() $r_1*c_1=r_1^{\prime}*c_1^{\prime}$,
$r_1*c_1=r_1^{\prime}*c_1^{\prime}$, ![]() $r_1*c_2=r_1^{\prime}*c_2^{\prime}$ and
$r_1*c_2=r_1^{\prime}*c_2^{\prime}$ and ![]() $r_2*c_1=r_2^{\prime}*c_1^{\prime}$, then it follows that
$r_2*c_1=r_2^{\prime}*c_1^{\prime}$, then it follows that ![]() $r_2*c_2=r_2'*c_2'$. For
$r_2*c_2=r_2'*c_2'$. For ![]() $|\mathbb F|=7$, we apply this criterion to the following quadrangles in
$|\mathbb F|=7$, we apply this criterion to the following quadrangles in ![]() $Q_{3,5}$:
$Q_{3,5}$:
 \begin{equation*} \begin{array}{r|cc} *&0&1\\ \hline 0&0&3\\
1&3&1 \end{array} \qquad \begin{array}{r|cc} *&6&5\\ \hline 2&0&3\\
4&3&0 \end{array} \end{equation*}
\begin{equation*} \begin{array}{r|cc} *&0&1\\ \hline 0&0&3\\
1&3&1 \end{array} \qquad \begin{array}{r|cc} *&6&5\\ \hline 2&0&3\\
4&3&0 \end{array} \end{equation*} It follows that ![]() $Q_{3,5}$ (and also, by Proposition 2.1(iv), its isomorph
$Q_{3,5}$ (and also, by Proposition 2.1(iv), its isomorph ![]() $Q_{5,3}$) is not isotopic to a group.
$Q_{5,3}$) is not isotopic to a group.
Similarly, for ![]() $|\mathbb F|=9$, the following quadrangles
$|\mathbb F|=9$, the following quadrangles
 \begin{equation*}
\begin{array}{r|cc}
*&1&2i\\
\hline
1&1&2\\
1+i&2&1
\end{array}
\qquad
\begin{array}{r|cc}
*&2+i&2+2i\\
\hline
1+2i&1&2\\
i&2&0
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{r|cc}
*&1&2i\\
\hline
1&1&2\\
1+i&2&1
\end{array}
\qquad
\begin{array}{r|cc}
*&2+i&2+2i\\
\hline
1+2i&1&2\\
i&2&0
\end{array}
\end{equation*} show that ![]() $Q_{1+i,1+2i}$ is not isotopic to any group (where
$Q_{1+i,1+2i}$ is not isotopic to any group (where ![]() $i=\sqrt{-1}$). This property is necessarily inherited by the opposite quasigroup
$i=\sqrt{-1}$). This property is necessarily inherited by the opposite quasigroup ![]() $Q_{2i,i}$ and translate
$Q_{2i,i}$ and translate ![]() $Q_{2+i,2+2i}$, as well as by
$Q_{2+i,2+2i}$, as well as by ![]() $Q_{1+2i,1+i}$,
$Q_{1+2i,1+i}$, ![]() $Q_{i,2i}$ and
$Q_{i,2i}$ and ![]() $Q_{2+2i,2+i}$. There are no other solutions to Condition (1.2) for
$Q_{2+2i,2+i}$. There are no other solutions to Condition (1.2) for ![]() $|\mathbb F|\leqslant9$.
$|\mathbb F|\leqslant9$.
If ![]() $|\mathbb F| \gt 9$, then let
$|\mathbb F| \gt 9$, then let ![]() $u,v\in\mathbb F$ be as given by Lemma 2.2. For such
$u,v\in\mathbb F$ be as given by Lemma 2.2. For such ![]() $u,v$, we have the following violation of the quadrangle criterion:
$u,v$, we have the following violation of the quadrangle criterion:
 \begin{equation*}
\begin{array}{r|cc}
*&u-bu&u-bu+1\\
\hline
-bu&0&b\\
1-bu&1-b&1
\end{array}
\qquad
\begin{array}{r|cc}
*&v-bv&v-bv+1\\
\hline
-bv&0&b\\
1-bv&1-a&1
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{r|cc}
*&u-bu&u-bu+1\\
\hline
-bu&0&b\\
1-bu&1-b&1
\end{array}
\qquad
\begin{array}{r|cc}
*&v-bv&v-bv+1\\
\hline
-bv&0&b\\
1-bv&1-a&1
\end{array}
\end{equation*}Lemma 2.4. Let ![]() $Q = Q_{a,b}$ be a quadratic quasigroup over
$Q = Q_{a,b}$ be a quadratic quasigroup over ![]() $\mathbb F$. If
$\mathbb F$. If ![]() $-1$ is a square, then Q is commutative if and only if
$-1$ is a square, then Q is commutative if and only if ![]() $a=b =1/2$. If
$a=b =1/2$. If ![]() $-1$ is a non-square, then Q is commutative if and only if
$-1$ is a non-square, then Q is commutative if and only if ![]() $a+b =1$.
$a+b =1$.
Proof. We use Proposition 2.1(v). If ![]() $|\mathbb F|\equiv1\bmod4$, then
$|\mathbb F|\equiv1\bmod4$, then ![]() $Q_{a,b}$ is commutative if and only if
$Q_{a,b}$ is commutative if and only if ![]() $a=1-a$ and
$a=1-a$ and ![]() $b=1-b$. If
$b=1-b$. If ![]() $|\mathbb F|\equiv3\bmod4$, then
$|\mathbb F|\equiv3\bmod4$, then ![]() $Q_{a,b}$ is commutative if and only if
$Q_{a,b}$ is commutative if and only if ![]() $a=1-b$ and
$a=1-b$ and ![]() $b=1-a$. The result follows.
$b=1-a$. The result follows.
Lemma 2.5. Let ![]() $Q = Q_{a,b}$ be a quadratic quasigroup over
$Q = Q_{a,b}$ be a quadratic quasigroup over ![]() $\mathbb F$. The quasigroup Q is entropic (or left distributive or right distributive) if and only if a = b.
$\mathbb F$. The quasigroup Q is entropic (or left distributive or right distributive) if and only if a = b.
Proof. If a = b, then Q is entropic (this is a well-known fact that may be verified directly). Idempotent entropic quasigroups are left distributive since an idempotent entropic quasigroup fulfils ![]() $x\cdot yz = xx \cdot yz = xy\cdot xz$. By Proposition 2.1(v), it thus suffices to assume that Q is left distributive and show that then a = b.
$x\cdot yz = xx \cdot yz = xy\cdot xz$. By Proposition 2.1(v), it thus suffices to assume that Q is left distributive and show that then a = b.
Since the number of squares in ![]() $\mathbb F$ exceeds
$\mathbb F$ exceeds ![]() $|\mathbb F|/2$, the squares cannot form a subquasigroup of Q. Hence, there exist squares
$|\mathbb F|/2$, the squares cannot form a subquasigroup of Q. Hence, there exist squares ![]() $x,y\in \mathbb F$ such that
$x,y\in \mathbb F$ such that ![]() $x*y$ is a non-square. By Condition (1.1),
$x*y$ is a non-square. By Condition (1.1), ![]() $0*(x*y) = b(x*y)$. If a is a square, then
$0*(x*y) = b(x*y)$. If a is a square, then ![]() $(0*x) * (0*y) =ax * ay=a(x*y)$, by Proposition 2.1(iii). Thus, in this case, the left distributivity clearly implies a = b. If a is a non-square, then b is a non-square too. If
$(0*x) * (0*y) =ax * ay=a(x*y)$, by Proposition 2.1(iii). Thus, in this case, the left distributivity clearly implies a = b. If a is a non-square, then b is a non-square too. If ![]() $a\ne b$, then
$a\ne b$, then ![]() $0*(x*y)=b(x*y)\ne bx * by = (0*x)*(0*y)$ by Proposition 2.1(vii).
$0*(x*y)=b(x*y)\ne bx * by = (0*x)*(0*y)$ by Proposition 2.1(vii).
A quasigroup ![]() $(M,\circ)$ is said to be affine if
$(M,\circ)$ is said to be affine if ![]() $x\circ y=x+\varphi(y-x)$ for all
$x\circ y=x+\varphi(y-x)$ for all ![]() $x,y\in M$, where
$x,y\in M$, where ![]() $\varphi\in\operatorname{Aut}(M)$ for some abelian group defined on M. An affine quasigroup is isotopic to the abelian group
$\varphi\in\operatorname{Aut}(M)$ for some abelian group defined on M. An affine quasigroup is isotopic to the abelian group ![]() $(M,+)$ since
$(M,+)$ since ![]() $x\circ y = (1-\varphi)(x) + \varphi(y)$. By Lemma 2.3,
$x\circ y = (1-\varphi)(x) + \varphi(y)$. By Lemma 2.3, ![]() $Q_{a,b}$ is isotopic to a group if and only if a = b. If a = b, then
$Q_{a,b}$ is isotopic to a group if and only if a = b. If a = b, then ![]() $Q_{a,b}$ is affine. We will say that
$Q_{a,b}$ is affine. We will say that ![]() $Q_{a,b}$ is non-affine if
$Q_{a,b}$ is non-affine if ![]() $a\ne b$.
$a\ne b$.
Lemma 2.6. Let ![]() $Q = Q_{a,b}$ be a quadratic quasigroup over
$Q = Q_{a,b}$ be a quadratic quasigroup over ![]() $\mathbb F$. The quasigroup Q is semisymmetric if and only if
$\mathbb F$. The quasigroup Q is semisymmetric if and only if ![]() $a^2-a+1=0$ and either a = b or
$a^2-a+1=0$ and either a = b or ![]() $a+b=1$.
$a+b=1$.
Proof. We use Proposition 2.1(vi) and the fact that ![]() $Q_{a,b}$ is semisymmetric if and only if it equals its translate. First suppose that
$Q_{a,b}$ is semisymmetric if and only if it equals its translate. First suppose that ![]() $\chi(a)\ne\chi(-1)$. Then
$\chi(a)\ne\chi(-1)$. Then ![]() $Q_{a,b}$ equals its translate if and only if
$Q_{a,b}$ equals its translate if and only if ![]() $a-1=ab=b-1$, which is equivalent to
$a-1=ab=b-1$, which is equivalent to ![]() $a=b=a^2+1$. Next suppose that
$a=b=a^2+1$. Next suppose that ![]() $\chi(a)=\chi(-1)$. Then
$\chi(a)=\chi(-1)$. Then ![]() $Q_{a,b}$ equals its translate if and only if
$Q_{a,b}$ equals its translate if and only if ![]() $a,b$ are both solutions to
$a,b$ are both solutions to ![]() $x=(x-1)/x$. There are two possibilities. The first is that
$x=(x-1)/x$. There are two possibilities. The first is that ![]() $a=b=a^2+1$. The second is that
$a=b=a^2+1$. The second is that ![]() $a,b$ are the two distinct roots of
$a,b$ are the two distinct roots of ![]() $x^2-x+1=0$, in which case
$x^2-x+1=0$, in which case ![]() $a+b=1$. The result now follows from the observation that if
$a+b=1$. The result now follows from the observation that if ![]() $a^2-a+1=0$ and
$a^2-a+1=0$ and ![]() $a+b=1$, then
$a+b=1$, then ![]() $\chi(a)=\chi(b)=\chi(-a^2)=\chi(-1)$.
$\chi(a)=\chi(b)=\chi(-a^2)=\chi(-1)$.
Lemma 2.7. Let ![]() $Q=Q_{a,b}$ be a quadratic quasigroup over
$Q=Q_{a,b}$ be a quadratic quasigroup over ![]() $\mathbb F$. If
$\mathbb F$. If ![]() $\operatorname{char}(\mathbb F) = 3$, then Q is a Steiner quasigroup if and only if
$\operatorname{char}(\mathbb F) = 3$, then Q is a Steiner quasigroup if and only if ![]() $a=b=-1$. In such a case, Q is induced by an affine STS. If
$a=b=-1$. In such a case, Q is induced by an affine STS. If ![]() $\operatorname{char}(\mathbb F)\ne 3$, then Q is a Steiner quasigroup if and only if
$\operatorname{char}(\mathbb F)\ne 3$, then Q is a Steiner quasigroup if and only if ![]() $ab= 1 =a+b$ and
$ab= 1 =a+b$ and ![]() $-1$ is a non-square. In such a case, we have
$-1$ is a non-square. In such a case, we have ![]() $a\ne b$,
$a\ne b$,
 \begin{equation}
\begin{gathered}
ab=a+b=a-a^2=b-b^2=-a^3=-b^3=1\text{ and }\\
\chi(a)=\chi(b)=\chi(1-a)=\chi(1-b)=\chi(-1) = -1.
\end{gathered}
\end{equation}
\begin{equation}
\begin{gathered}
ab=a+b=a-a^2=b-b^2=-a^3=-b^3=1\text{ and }\\
\chi(a)=\chi(b)=\chi(1-a)=\chi(1-b)=\chi(-1) = -1.
\end{gathered}
\end{equation} If ![]() $Q_{a,b}$ is a non-affine Steiner quasigroup, then
$Q_{a,b}$ is a non-affine Steiner quasigroup, then ![]() $Q_{c,d}$ is another non-affine quadratic Steiner quasigroup over
$Q_{c,d}$ is another non-affine quadratic Steiner quasigroup over ![]() $\mathbb F$ if and only if
$\mathbb F$ if and only if ![]() $\{a,b\} = \{c,d\}$. In such a case,
$\{a,b\} = \{c,d\}$. In such a case, ![]() $Q_{a,b}\cong Q_{c,d}$.
$Q_{a,b}\cong Q_{c,d}$.
Proof. Since total symmetry is the combination of semi-symmetry with commutativity, we combine Lemmas 2.6 and 2.4. Together they imply that the necessary and sufficient conditions for total symmetry are that at least one of
Condition (2.3) implies that ![]() $a(1-b)-a=-1$ and hence ab = 1. Moreover, if ab = 1 and
$a(1-b)-a=-1$ and hence ab = 1. Moreover, if ab = 1 and ![]() $a+b=1$, then
$a+b=1$, then ![]() $a^2=a(1-b)=a-1$. The characterization of quadratic Steiner quasigroups follows.
$a^2=a(1-b)=a-1$. The characterization of quadratic Steiner quasigroups follows.
Assume Condition (2.3) holds. Then ![]() $b-b^2=b(1-b)=(1-a)a=1$. So
$b-b^2=b(1-b)=(1-a)a=1$. So ![]() $a,b$ are both roots of
$a,b$ are both roots of ![]() $x^2-x+1=0$ and hence also of
$x^2-x+1=0$ and hence also of ![]() $x^3+1=(x+1)(x^2-x+1)=0$. From
$x^3+1=(x+1)(x^2-x+1)=0$. From ![]() $a^3=b^3=-1$ and
$a^3=b^3=-1$ and ![]() $a+b=1$, we get
$a+b=1$, we get ![]() $\chi(a)=\chi(b)=\chi(-1)=\chi(1-b)=\chi(1-a)$.
$\chi(a)=\chi(b)=\chi(-1)=\chi(1-b)=\chi(1-a)$.
The polynomial ![]() $x^2-x+1$ has at most two roots (these roots coincide if and only if
$x^2-x+1$ has at most two roots (these roots coincide if and only if ![]() $\operatorname{char}(\mathbb F) = 3$). That explains why
$\operatorname{char}(\mathbb F) = 3$). That explains why ![]() $\{a,b\} = \{c,d\}$ if
$\{a,b\} = \{c,d\}$ if ![]() $Q_{a,b}$ and
$Q_{a,b}$ and ![]() $Q_{c,d}$ are Steiner quadratic quasigroups on
$Q_{c,d}$ are Steiner quadratic quasigroups on ![]() $\mathbb F$, with
$\mathbb F$, with ![]() $a\ne b$ and
$a\ne b$ and ![]() $c\ne d$. If
$c\ne d$. If ![]() $\{a,b\} = \{c,d\}$, then
$\{a,b\} = \{c,d\}$, then ![]() $Q_{a,b}\cong Q_{c,d}$ by Proposition 2.1(iv).
$Q_{a,b}\cong Q_{c,d}$ by Proposition 2.1(iv).
For the next proof, we define notation θx by ![]() $\theta_{x}=a$ if
$\theta_{x}=a$ if ![]() $\chi(x)=1$ and
$\chi(x)=1$ and ![]() $\theta_{x}=b$ if
$\theta_{x}=b$ if ![]() $\chi(x)=-1$. Note that
$\chi(x)=-1$. Note that ![]() $\theta_{a}=\theta_{b}$ and
$\theta_{a}=\theta_{b}$ and ![]() $\theta_{1-a}=\theta_{1-b}$ for any quadratic quasigroup
$\theta_{1-a}=\theta_{1-b}$ for any quadratic quasigroup ![]() $Q_{a,b}$.
$Q_{a,b}$.
Lemma 2.8. The quadratic quasigroup ![]() $Q=Q_{a,b}$ is flexible if and only if at least one of the following conditions holds:
$Q=Q_{a,b}$ is flexible if and only if at least one of the following conditions holds:
(i) a = b,
(ii)
 $\chi(a) = \chi(1-a)=1$, or
$\chi(a) = \chi(1-a)=1$, or(iii)
 $a+b=1$ and
$a+b=1$ and  $|\mathbb F|\equiv3\bmod4$.
$|\mathbb F|\equiv3\bmod4$.
Proof. First note that ![]() $x*(x*x)=x*x=(x*x)*x$ for all
$x*(x*x)=x*x=(x*x)*x$ for all ![]() $x\in\mathbb F$, by idempotence. Thus, consider distinct
$x\in\mathbb F$, by idempotence. Thus, consider distinct ![]() $x,y\in \mathbb F$ and let
$x,y\in \mathbb F$ and let ![]() $z=x-y$. Then
$z=x-y$. Then
and
It follows that Q is flexible if and only if
for all z. Both sides of Condition (2.4) are members of ![]() $\Phi=\{a(a-1),a(b-1),b(a-1),b(b-1)\}$. If a = b, then
$\Phi=\{a(a-1),a(b-1),b(a-1),b(b-1)\}$. If a = b, then ![]() $|\Phi|=1$, so Condition (2.4) is automatically satisfied. Henceforth, we assume
$|\Phi|=1$, so Condition (2.4) is automatically satisfied. Henceforth, we assume ![]() $a\ne b$. In this case,
$a\ne b$. In this case, ![]() $|\Phi|=4$ unless
$|\Phi|=4$ unless ![]() $a(a-1)=b(b-1)$, which requires
$a(a-1)=b(b-1)$, which requires ![]() $a=1-b$.
$a=1-b$.
Suppose for the moment that ![]() $\chi(z)=1$, meaning that Condition (2.4) is equivalent to
$\chi(z)=1$, meaning that Condition (2.4) is equivalent to ![]() $\theta_{a-1}(a-1)=\theta_{-1}(\theta_{a}-1)$. From the above observations, this condition can only be satisfied if
$\theta_{a-1}(a-1)=\theta_{-1}(\theta_{a}-1)$. From the above observations, this condition can only be satisfied if
Now Condition (2.5) is equivalent to condition (ii), whereas Condition (2.6) implies (iii). It follows that for ![]() $Q_{a,b}$ to be flexible, it is necessary that (i), (ii) or (iii) holds.
$Q_{a,b}$ to be flexible, it is necessary that (i), (ii) or (iii) holds.
To check sufficiency, we first note that if (iii) is true, then ![]() $\chi(a)=\chi(1-a)$, so either (ii) or Condition (2.6) holds. Hence, if (ii) or (iii) holds, then at least one of Conditions (2.5) or (2.6) holds. Moreover, Condition (2.5) implies that
$\chi(a)=\chi(1-a)$, so either (ii) or Condition (2.6) holds. Hence, if (ii) or (iii) holds, then at least one of Conditions (2.5) or (2.6) holds. Moreover, Condition (2.5) implies that ![]() $\theta_{z(a-1)}=\theta_{-z}$ and
$\theta_{z(a-1)}=\theta_{-z}$ and ![]() $\theta_{z}=\theta_{az}$, whereas Condition (2.6) implies that
$\theta_{z}=\theta_{az}$, whereas Condition (2.6) implies that ![]() $\theta_{-z}=1-\theta_{z}$ and
$\theta_{-z}=1-\theta_{z}$ and ![]() $\theta_{az}=\theta_{(1-a)z}=1-\theta_{z(a-1)}$. In either case, Condition (2.4) holds for all z.
$\theta_{az}=\theta_{(1-a)z}=1-\theta_{z(a-1)}$. In either case, Condition (2.4) holds for all z.
We note in passing that idempotent entropic quasigroups are always flexible because ![]() $x(yx) = (xx)(yx) = (xy)(xx) = (xy)x$. Commutative quasigroups are flexible too because
$x(yx) = (xx)(yx) = (xy)(xx) = (xy)x$. Commutative quasigroups are flexible too because ![]() $x(yx) = (yx)x = (xy)x$. These two facts support the observation that the conditions encountered in Lemmas 2.5 and 2.4 are incorporated in Lemma 2.8.
$x(yx) = (yx)x = (xy)x$. These two facts support the observation that the conditions encountered in Lemmas 2.5 and 2.4 are incorporated in Lemma 2.8.
3. Subquasigroups and affine automorphisms
If Q is an idempotent quasigroup, then the term trivial subquasigroup refers to a quasigroup consisting of at most one element. A minimal subquasigroup is a non-trivial subquasigroup in which all proper subquasigroups are trivial. A 2-generated subquasigroup is a subquasigroup S for which there exists ![]() $A\subseteq S$ such that
$A\subseteq S$ such that ![]() $|A|\leqslant 2$ and S is the smallest subquasigroup of Q that contains A. Any 2-element subset of a minimal subquasigroup S generates S. However, there may exist non-trivial 2-generated subquasigroups that are not minimal.
$|A|\leqslant 2$ and S is the smallest subquasigroup of Q that contains A. Any 2-element subset of a minimal subquasigroup S generates S. However, there may exist non-trivial 2-generated subquasigroups that are not minimal.
The field ![]() $\mathbb F$ is a vector space over its prime field. Saying that
$\mathbb F$ is a vector space over its prime field. Saying that ![]() $U\subseteq \mathbb F$ is a subspace (of
$U\subseteq \mathbb F$ is a subspace (of ![]() $\mathbb F$) means that it is a subspace of that vector space.
$\mathbb F$) means that it is a subspace of that vector space.
The purpose of this section is to show that if ![]() $Q_{a,b}$ is not a Steiner quasigroup, then each minimal subquasigroup of
$Q_{a,b}$ is not a Steiner quasigroup, then each minimal subquasigroup of ![]() $Q_{a,b}$ is formed by a coset of a subspace of
$Q_{a,b}$ is formed by a coset of a subspace of ![]() $\mathbb F$. In particular, if a minimal subquasigroup contains zero, then it is closed under addition.
$\mathbb F$. In particular, if a minimal subquasigroup contains zero, then it is closed under addition.
We start by two auxiliary observations that concern Frobenius groups.
Lemma 3.1. Let G be a Frobenius group that acts naturally on a finite set Ω. If Gω contains at most two non-trivial orbits for some ![]() $\omega \in \Omega$, then the Frobenius kernel of G is an elementary abelian group.
$\omega \in \Omega$, then the Frobenius kernel of G is an elementary abelian group.
Proof. Put ![]() $n=|\Omega|$. By the assumptions there exists an orbit Γ of Gω such that
$n=|\Omega|$. By the assumptions there exists an orbit Γ of Gω such that ![]() $|\Gamma|+1 \gt n/2$. This implies that G is primitive. Now, elements of Ω may be identified with elements of a group N (which is isomorphic to the Frobenius kernel), and Gω may be identified with a subgroup of
$|\Gamma|+1 \gt n/2$. This implies that G is primitive. Now, elements of Ω may be identified with elements of a group N (which is isomorphic to the Frobenius kernel), and Gω may be identified with a subgroup of ![]() $\operatorname{Aut}(N)$. Since there are at most two nontrivial orbits of Gω, there are at most two integers that occur as an order of a non-trivial element of N. One of these integers has to be a prime, and the other (if it exists) is either a square of this prime or another prime. This means that N is solvable. A finite solvable group is either elementary abelian or it contains a non-trivial proper characteristic subgroup. However, such a subgroup yields a block
$\operatorname{Aut}(N)$. Since there are at most two nontrivial orbits of Gω, there are at most two integers that occur as an order of a non-trivial element of N. One of these integers has to be a prime, and the other (if it exists) is either a square of this prime or another prime. This means that N is solvable. A finite solvable group is either elementary abelian or it contains a non-trivial proper characteristic subgroup. However, such a subgroup yields a block ![]() $B\subseteq \Omega$. That is not possible since G is primitive.
$B\subseteq \Omega$. That is not possible since G is primitive.
Lemma 3.2. Let G be a Frobenius group that acts naturally on a finite set Ω. Suppose that the Frobenius complement of G is abelian. If ![]() $\alpha,\beta\in \Omega$,
$\alpha,\beta\in \Omega$, ![]() $\alpha \ne \beta$,
$\alpha \ne \beta$, ![]() $\varphi\in G_\alpha$,
$\varphi\in G_\alpha$, ![]() $\psi\in G_\beta$ and
$\psi\in G_\beta$ and ![]() $\operatorname{id}_\Omega
\notin \{\varphi,\psi\}$, then
$\operatorname{id}_\Omega
\notin \{\varphi,\psi\}$, then ![]() $[\varphi,\varphi^{\psi}]$ is fixed point free.
$[\varphi,\varphi^{\psi}]$ is fixed point free.
Proof. Denote by N the Frobenius kernel of G and recall that non-identity elements of N act without fixed points. Since ![]() $G/N$ is abelian, we must have
$G/N$ is abelian, we must have ![]() $[g,h]\in N$ for any
$[g,h]\in N$ for any ![]() $g,h\in G$. To prove that
$g,h\in G$. To prove that ![]() $[g,h]$ is fixed point free, it therefore suffices to find any
$[g,h]$ is fixed point free, it therefore suffices to find any ![]() $\omega\in \Omega$ such that
$\omega\in \Omega$ such that ![]() $gh(\omega) \ne hg(\omega)$. We take
$gh(\omega) \ne hg(\omega)$. We take ![]() $\omega=\psi^{-1}(\alpha)$ and observe that
$\omega=\psi^{-1}(\alpha)$ and observe that
Suppose that ![]() $\psi(\varphi\omega)=\varphi\psi(\varphi\omega)$. By definition, α is the only fixed point of φ and β is the only fixed point of ψ, so we can deduce in turn that
$\psi(\varphi\omega)=\varphi\psi(\varphi\omega)$. By definition, α is the only fixed point of φ and β is the only fixed point of ψ, so we can deduce in turn that ![]() $\psi(\varphi\omega)=\alpha$,
$\psi(\varphi\omega)=\alpha$, ![]() $\varphi\omega =\omega$,
$\varphi\omega =\omega$, ![]() $\omega = \alpha$,
$\omega = \alpha$, ![]() $\psi(\alpha)=\alpha$ and thus
$\psi(\alpha)=\alpha$ and thus ![]() $\alpha = \beta$. This contradiction proves that
$\alpha = \beta$. This contradiction proves that ![]() $\varphi\varphi^\psi(\omega)\ne\varphi^\psi\varphi(\omega)$, from which the result follows.
$\varphi\varphi^\psi(\omega)\ne\varphi^\psi\varphi(\omega)$, from which the result follows.
A mapping ![]() $x\mapsto ux + v$, with
$x\mapsto ux + v$, with ![]() $u \in \mathbb F^*$ and
$u \in \mathbb F^*$ and ![]() $v\in\mathbb F$, is said to be an affine permutation of
$v\in\mathbb F$, is said to be an affine permutation of ![]() $\mathbb F$. Affine permutations form a sharply 2-transitive group. Those with u a square form a subgroup of
$\mathbb F$. Affine permutations form a sharply 2-transitive group. Those with u a square form a subgroup of ![]() $\operatorname{Aut}(Q)$, for any quadratic quasigroup
$\operatorname{Aut}(Q)$, for any quadratic quasigroup ![]() $Q=Q_{a,b}$ over
$Q=Q_{a,b}$ over ![]() $\mathbb F$, by Proposition 2.1(ii),(iii). Hence, we have:
$\mathbb F$, by Proposition 2.1(ii),(iii). Hence, we have:
Proposition 3.3. Suppose that ![]() $Q=Q_{a,b}$ is a quadratic quasigroup over
$Q=Q_{a,b}$ is a quadratic quasigroup over ![]() $\mathbb F$. Let
$\mathbb F$. Let ![]() $s,t,u,v\in \mathbb F$ be such that
$s,t,u,v\in \mathbb F$ be such that ![]() $\chi(s-t) = \chi(u-v)$. Then there exists an affine automorphism
$\chi(s-t) = \chi(u-v)$. Then there exists an affine automorphism ![]() $\alpha\in \operatorname{Aut}(Q)$ such that
$\alpha\in \operatorname{Aut}(Q)$ such that ![]() $\alpha(s) = u$ and
$\alpha(s) = u$ and ![]() $\alpha(t) = v$.
$\alpha(t) = v$.
Proof. If s = t, then u = v, so we may use ![]() $x\mapsto x+u-s$ for α. So assume
$x\mapsto x+u-s$ for α. So assume ![]() $t\ne s$, meaning that
$t\ne s$, meaning that ![]() $u\ne v$ as well. Put
$u\ne v$ as well. Put ![]() $\lambda = (u-v)/(s-t)$ and
$\lambda = (u-v)/(s-t)$ and ![]() $\mu = (vs-ut)/(s-t)$. The mapping
$\mu = (vs-ut)/(s-t)$. The mapping ![]() $x \mapsto \lambda x + \mu$ is an automorphism of
$x \mapsto \lambda x + \mu$ is an automorphism of ![]() $Q_{a,b}$ that sends s to u and t to v.
$Q_{a,b}$ that sends s to u and t to v.
Proposition 3.4. Suppose that ![]() $Q = Q_{a,b}$. If
$Q = Q_{a,b}$. If ![]() $\operatorname{char}(\mathbb F) = 3$, then each minimal subquasigroup of Q is a coset of a subspace of
$\operatorname{char}(\mathbb F) = 3$, then each minimal subquasigroup of Q is a coset of a subspace of ![]() $\mathbb F$. If
$\mathbb F$. If ![]() $\operatorname{char}(\mathbb F)\ne 3$, then each minimal subquasigroup of Q is either a coset of a subspace of
$\operatorname{char}(\mathbb F)\ne 3$, then each minimal subquasigroup of Q is either a coset of a subspace of ![]() $\mathbb F$, or Condition (2.1) holds.
$\mathbb F$, or Condition (2.1) holds.
Proof. Let U be a minimal subquasigroup of Q. Set ![]() $m = |U|$. For
$m = |U|$. For ![]() $\varepsilon\in \{-1,1\}$, denote by
$\varepsilon\in \{-1,1\}$, denote by ![]() $\sigma(\varepsilon)$ the number of
$\sigma(\varepsilon)$ the number of ![]() $(u,v)\in U\times U$ such that
$(u,v)\in U\times U$ such that ![]() $\chi(v-u) = \varepsilon$. Since
$\chi(v-u) = \varepsilon$. Since ![]() $\sigma(1)+\sigma(-1)=m(m-1)$, there exists
$\sigma(1)+\sigma(-1)=m(m-1)$, there exists ![]() $\varepsilon\in \{-1,1\}$ such that
$\varepsilon\in \{-1,1\}$ such that  $\sigma(\varepsilon)\geqslant \binom
m2$. Fix such ɛ, and fix also
$\sigma(\varepsilon)\geqslant \binom
m2$. Fix such ɛ, and fix also ![]() $s,t \in U$ such that
$s,t \in U$ such that ![]() $\chi(t-s)=\varepsilon$.
$\chi(t-s)=\varepsilon$.
Denote by A the permutation group on U that is induced by affine automorphisms acting on U. Since s and t generate U, we see that ![]() $\psi(U) = U$ whenever
$\psi(U) = U$ whenever ![]() $\psi \in \operatorname{Aut}(Q)$ is such that
$\psi \in \operatorname{Aut}(Q)$ is such that ![]() $\psi(s),\psi(t)\in U$. By Proposition 3.3, for each
$\psi(s),\psi(t)\in U$. By Proposition 3.3, for each ![]() $(u,v) \in U\times U$ with
$(u,v) \in U\times U$ with ![]() $\chi(v-u)=\varepsilon$, there exists
$\chi(v-u)=\varepsilon$, there exists ![]() $\psi \in A$ such that
$\psi \in A$ such that ![]() $\psi(s) = u$ and
$\psi(s) = u$ and ![]() $\psi(t) = v$. Therefore,
$\psi(t) = v$. Therefore,  $|A|\geqslant \binom m2$.
$|A|\geqslant \binom m2$.
Denote by f the number of fixed point free elements of A. The aggregate number of fixed points of elements of A is equal to ![]() $m+|A| - 1 -f$. By Burnside’s lemma, this is equal to
$m+|A| - 1 -f$. By Burnside’s lemma, this is equal to ![]() $|A|k$, where k is the number of orbits of A. If
$|A|k$, where k is the number of orbits of A. If ![]() $k\geqslant 2$, then
$k\geqslant 2$, then
 \begin{equation*}m-1-f = |A|(k - 1) \geqslant|A|\geqslant \frac{1}{2} m(m-1).\end{equation*}
\begin{equation*}m-1-f = |A|(k - 1) \geqslant|A|\geqslant \frac{1}{2} m(m-1).\end{equation*} It follows that ![]() $2(-1-f) \geqslant m(m-3)$, and hence m < 3. However, this is impossible since there is no idempotent quasigroup of order two and
$2(-1-f) \geqslant m(m-3)$, and hence m < 3. However, this is impossible since there is no idempotent quasigroup of order two and ![]() $|U| \gt 1$. Hence, k = 1; in other words, A is transitive. As each non-trivial element of A fixes at most one element, it follows that A is either a regular group or a Frobenius group. Since
$|U| \gt 1$. Hence, k = 1; in other words, A is transitive. As each non-trivial element of A fixes at most one element, it follows that A is either a regular group or a Frobenius group. Since ![]() $|A| \geqslant m(m-1)/2$, the former alternative may take place if and only if m = 3. We distinguish two cases.
$|A| \geqslant m(m-1)/2$, the former alternative may take place if and only if m = 3. We distinguish two cases.
First, suppose that ![]() $|A|=3$. This means that A is cyclic, and
$|A|=3$. This means that A is cyclic, and ![]() $|U|=m=3$ as well. Let A be generated by an affine permutation
$|U|=m=3$ as well. Let A be generated by an affine permutation ![]() $x\mapsto \lambda x +\mu$. If λ = 1, then U is a coset of a subspace and
$x\mapsto \lambda x +\mu$. If λ = 1, then U is a coset of a subspace and ![]() $\operatorname{char}(\mathbb F)=3$. Suppose
$\operatorname{char}(\mathbb F)=3$. Suppose ![]() $\lambda \ne 1$. Then
$\lambda \ne 1$. Then ![]() $\lambda^3 = 1$, so
$\lambda^3 = 1$, so ![]() $\lambda^2 + \lambda + 1=0$. Our intention is to show that
$\lambda^2 + \lambda + 1=0$. Our intention is to show that ![]() $ab = 1 = a+b$. By Proposition 2.1(ii), it may be assumed that
$ab = 1 = a+b$. By Proposition 2.1(ii), it may be assumed that ![]() $0 \in U$ since automorphisms map minimal subquasigroups to minimal subquasigroups. Suppose that
$0 \in U$ since automorphisms map minimal subquasigroups to minimal subquasigroups. Suppose that ![]() $u \in U\setminus\{0\}$. Then
$u \in U\setminus\{0\}$. Then ![]() $u=\mu$ and
$u=\mu$ and ![]() $U=\{0,u,(\lambda+1)u\}$. Since U is idempotent,
$U=\{0,u,(\lambda+1)u\}$. Since U is idempotent, ![]() $u*0=0*u = (\lambda+1)u = -\lambda^2 u$. Suppose that −1 is a square. Then
$u*0=0*u = (\lambda+1)u = -\lambda^2 u$. Suppose that −1 is a square. Then ![]() $-\lambda^2u=u*0=u-0*u=(1+\lambda^2)u=-\lambda u$, resulting in λ = 1. Hence, −1 is a non-square. If u is a square, then
$-\lambda^2u=u*0=u-0*u=(1+\lambda^2)u=-\lambda u$, resulting in λ = 1. Hence, −1 is a non-square. If u is a square, then ![]() $0*u=au$, so
$0*u=au$, so ![]() $a=-\lambda^2$ and
$a=-\lambda^2$ and ![]() $u=0*(-\lambda^2 u) = -\lambda^2 bu = abu$. Alternatively, if u is a non-square, then
$u=0*(-\lambda^2 u) = -\lambda^2 bu = abu$. Alternatively, if u is a non-square, then ![]() $0*u=bu$, so
$0*u=bu$, so ![]() $b=-\lambda^2$ and
$b=-\lambda^2$ and ![]() $u=0*(-\lambda^2 u) = -\lambda^2 au = abu$. Therefore, ab = 1 in every case. Since at least one of a 3 and b 3 is equal to
$u=0*(-\lambda^2 u) = -\lambda^2 au = abu$. Therefore, ab = 1 in every case. Since at least one of a 3 and b 3 is equal to ![]() $(-\lambda^2)^3 = - 1$, it must be that
$(-\lambda^2)^3 = - 1$, it must be that ![]() $a^3 = -1 =b^3$.
$a^3 = -1 =b^3$.
Thus, ![]() $\chi(a) = \chi(b) = \chi(-1) = -1$ and
$\chi(a) = \chi(b) = \chi(-1) = -1$ and ![]() $0 = a^3+1=(a+1)(a^2-a+1)$. If
$0 = a^3+1=(a+1)(a^2-a+1)$. If ![]() $a = -1$, then
$a = -1$, then ![]() $b=-1$ and
$b=-1$ and ![]() $-u = 0*u=u * 0 = u -(-u) = 2u$. In such a case,
$-u = 0*u=u * 0 = u -(-u) = 2u$. In such a case, ![]() $0 = 3$,
$0 = 3$, ![]() $U = \{0,u,-u\}$ is a subspace of
$U = \{0,u,-u\}$ is a subspace of ![]() $\mathbb F$, and
$\mathbb F$, and ![]() $a+b = - 2=1$. Assume
$a+b = - 2=1$. Assume ![]() $a\ne -1$. Then
$a\ne -1$. Then ![]() $b\ne -1$,
$b\ne -1$, ![]() $a^2-a=-1=b^2-b$ and
$a^2-a=-1=b^2-b$ and ![]() $a+b = a+a^{-1} = (a^2+1)/a=1$. Hence, Condition (2.1) holds, by Lemma 2.7.
$a+b = a+a^{-1} = (a^2+1)/a=1$. Hence, Condition (2.1) holds, by Lemma 2.7.
Let us now turn to the case ![]() $|A| \gt 3$. The group A is a Frobenius group on an m-element set U with complements of order
$|A| \gt 3$. The group A is a Frobenius group on an m-element set U with complements of order ![]() $\geqslant (m-1)/2$. The kernel of A is elementary abelian, by Lemma 3.1. To finish it suffices to prove that all elements of the kernel of A are induced by translations
$\geqslant (m-1)/2$. The kernel of A is elementary abelian, by Lemma 3.1. To finish it suffices to prove that all elements of the kernel of A are induced by translations ![]() $x\mapsto x+\mu$. Assume the contrary. This means that the kernel of A contains a permutation that is a restriction of an affine automorphism
$x\mapsto x+\mu$. Assume the contrary. This means that the kernel of A contains a permutation that is a restriction of an affine automorphism ![]() $\psi\colon x\mapsto \lambda x + \mu$, where
$\psi\colon x\mapsto \lambda x + \mu$, where ![]() $\lambda\ne1$. Choose an affine automorphism φ that induces a non-trivial permutation belonging to a complement of A. Both φ and ψ are elements of the Frobenius group formed by affine automorphisms of Q, and they belong to different Frobenius complements of the latter group. Hence,
$\lambda\ne1$. Choose an affine automorphism φ that induces a non-trivial permutation belonging to a complement of A. Both φ and ψ are elements of the Frobenius group formed by affine automorphisms of Q, and they belong to different Frobenius complements of the latter group. Hence, ![]() $[\psi,\psi^\varphi]$ is a fixed point free permutation of Q, by Lemma 3.2. Denote by
$[\psi,\psi^\varphi]$ is a fixed point free permutation of Q, by Lemma 3.2. Denote by ![]() $\tilde \psi$ the restriction of ψ to A. Both
$\tilde \psi$ the restriction of ψ to A. Both ![]() $\tilde \psi$ and
$\tilde \psi$ and ![]() $\tilde \psi^\varphi$ belong to the kernel of A. This kernel is abelian. Hence,
$\tilde \psi^\varphi$ belong to the kernel of A. This kernel is abelian. Hence, ![]() $[\psi,\psi^\varphi]$ fixes each point of U, a contradiction.
$[\psi,\psi^\varphi]$ fixes each point of U, a contradiction.
4. Existence and non-existence of isomorphisms
The purpose of this section is to prove Theorems 1.1 and 1.2 for 2-generated quadratic quasigroups and to discuss consequences of the existence of an additive automorphism ![]() $\varphi\in \operatorname{Aut}(Q)$ that maps a square to a non-square. One of the tools will be the following obvious fact:
$\varphi\in \operatorname{Aut}(Q)$ that maps a square to a non-square. One of the tools will be the following obvious fact:
Lemma 4.1. Let ![]() $x\in \mathbb F^*$. The least subfield containing x coincides with the set of all sums
$x\in \mathbb F^*$. The least subfield containing x coincides with the set of all sums ![]() $x^{i_1}+\cdots + x^{i_k}$, where ij is a non-negative integer for
$x^{i_1}+\cdots + x^{i_k}$, where ij is a non-negative integer for ![]() $1\leqslant j \leqslant k$ and
$1\leqslant j \leqslant k$ and ![]() $k \geqslant 0$.
$k \geqslant 0$.
The following easy facts may be deduced, e.g., from results of Perron [Reference Perron10]. (To avoid a misunderstanding, let it be mentioned that while Perron’s paper is formulated for prime fields only, the proofs of the paper carry without a change to any finite field of odd order.)
Lemma 4.2. Assume ![]() $|\mathbb F|\geqslant 5$. Each square may be obtained as a sum of two non-squares, and each non-square may be obtained as a sum of two squares. For each
$|\mathbb F|\geqslant 5$. Each square may be obtained as a sum of two non-squares, and each non-square may be obtained as a sum of two squares. For each ![]() $a\in \mathbb F$, there exist squares
$a\in \mathbb F$, there exist squares ![]() $x,y\in \mathbb F$ and non-squares
$x,y\in \mathbb F$ and non-squares ![]() $x^{\prime},y^{\prime}\in \mathbb F$ such that a + x and
$x^{\prime},y^{\prime}\in \mathbb F$ such that a + x and ![]() $a+x^{\prime}$ are squares, while a + y and
$a+x^{\prime}$ are squares, while a + y and ![]() $a+y^{\prime}$ are non-squares.
$a+y^{\prime}$ are non-squares.
Note that if ![]() $Q_{a,b}$ is a quadratic quasigroup over
$Q_{a,b}$ is a quadratic quasigroup over ![]() $\mathbb F_3$, then
$\mathbb F_3$, then ![]() $a=b=-1$. In particular, if
$a=b=-1$. In particular, if ![]() $|\mathbb F| \lt 5$, then
$|\mathbb F| \lt 5$, then ![]() $Q_{a,b}$ has to be affine.
$Q_{a,b}$ has to be affine.
A permutation ψ of ![]() $\mathbb F$ is said to be additive if
$\mathbb F$ is said to be additive if ![]() $\psi(x+y) = \psi(x)+\psi(y)$ for all
$\psi(x+y) = \psi(x)+\psi(y)$ for all ![]() $x,y \in \mathbb F$.
$x,y \in \mathbb F$.
Lemma 4.3. Let ![]() $Q=Q_{a,b}$ be a non-affine quadratic quasigroup over
$Q=Q_{a,b}$ be a non-affine quadratic quasigroup over ![]() $\mathbb F$, and let
$\mathbb F$, and let ![]() $\varphi \in \operatorname{Aut}(Q)$ be additive. Suppose that there exists
$\varphi \in \operatorname{Aut}(Q)$ be additive. Suppose that there exists ![]() $f\in \mathbb F$ such that
$f\in \mathbb F$ such that ![]() $\varphi(a^i) = b^if$ for each integer i. Then f is a non-square.
$\varphi(a^i) = b^if$ for each integer i. Then f is a non-square.
Furthermore, denote by U the least subfield of ![]() $\mathbb F$ that contains the subquasigroup generated by 0 and 1. Then U is a subquasigroup of Q containing a and b, and
$\mathbb F$ that contains the subquasigroup generated by 0 and 1. Then U is a subquasigroup of Q containing a and b, and ![]() $b=a^\gamma$ for some γ > 1 such that
$b=a^\gamma$ for some γ > 1 such that  $\gamma^2 \bigm| |\mathbb F|$ and
$\gamma^2 \bigm| |\mathbb F|$ and ![]() $\varphi(u) =u^\gamma f$ for each
$\varphi(u) =u^\gamma f$ for each ![]() $u\in U$.
$u\in U$.
If U contains an element that is a non-square in ![]() $\mathbb F$, then
$\mathbb F$, then  $(U,*) = (\mathbb F_{\gamma^2},*_a)$.
$(U,*) = (\mathbb F_{\gamma^2},*_a)$.
Proof. Since ![]() $0*1 = a$, we have
$0*1 = a$, we have ![]() $0*f=\varphi(0)*\varphi(1) = \varphi(a) = bf$. Therefore, f is a non-square.
$0*f=\varphi(0)*\varphi(1) = \varphi(a) = bf$. Therefore, f is a non-square.
Denote by Ua the subfield of ![]() $\mathbb F$ generated by a and by Ub the subfield of
$\mathbb F$ generated by a and by Ub the subfield of ![]() $\mathbb F$ generated by b. The field Ua coincides with the set of all sums
$\mathbb F$ generated by b. The field Ua coincides with the set of all sums ![]() $a^{i_1}+\dots +
a^{i_k}$,
$a^{i_1}+\dots +
a^{i_k}$, ![]() $k\geqslant 0$, by Lemma 4.1. The assumptions of the statement imply that
$k\geqslant 0$, by Lemma 4.1. The assumptions of the statement imply that
This means that the bijection φ maps Ua to Ubf. Therefore, there exists a bijection ![]() $\alpha\colon U_a\to U_b$ such that φ sends
$\alpha\colon U_a\to U_b$ such that φ sends ![]() $u\in U_a$ to
$u\in U_a$ to ![]() $\alpha(u)f$. The form of α follows from Condition (4.1), and this form stipulates that α is an isomorphism of fields
$\alpha(u)f$. The form of α follows from Condition (4.1), and this form stipulates that α is an isomorphism of fields ![]() $U_a \cong U_b$. Both of them are subfields of
$U_a \cong U_b$. Both of them are subfields of ![]() $\mathbb F$. Since they are of the same order, they have to coincide.
$\mathbb F$. Since they are of the same order, they have to coincide.
Note that any subfield that contains both a and b forms a subquasigroup of Q, by Condition (1.1). Hence, Ua is a subquasigroup that contains both 0 and 1. Therefore, ![]() $U_a \supseteq U$. Since
$U_a \supseteq U$. Since ![]() $0*1 =a \in U$, we have
$0*1 =a \in U$, we have ![]() $U\supseteq U_a$ as well, so
$U\supseteq U_a$ as well, so ![]() $U=U_a$.
$U=U_a$.
The field automorphism ![]() $\alpha \in \operatorname{Aut}(U)$ extends to an automorphism of
$\alpha \in \operatorname{Aut}(U)$ extends to an automorphism of ![]() $\mathbb F$ that sends each
$\mathbb F$ that sends each ![]() $x\in \mathbb F$ to x γ, where γ divides
$x\in \mathbb F$ to x γ, where γ divides ![]() $|U|$, which in turn divides
$|U|$, which in turn divides ![]() $|\mathbb F|$.
$|\mathbb F|$.
Every element of a subfield ![]() $\mathbb K$ of
$\mathbb K$ of ![]() $\mathbb F$ is a square in
$\mathbb F$ is a square in ![]() $\mathbb F$ if and only if
$\mathbb F$ if and only if ![]() $|\mathbb F:\mathbb K|$ is an even number. If
$|\mathbb F:\mathbb K|$ is an even number. If ![]() $|\mathbb F:U|$ is even, then γ 2 divides
$|\mathbb F:U|$ is even, then γ 2 divides ![]() $|\mathbb F|$.
$|\mathbb F|$.
Suppose that ![]() $|\mathbb F:U|$ is odd. Then there exists
$|\mathbb F:U|$ is odd. Then there exists ![]() $u\in U$ such that u is a non-square in
$u\in U$ such that u is a non-square in ![]() $\mathbb F$. Since
$\mathbb F$. Since ![]() $0*u = bu=a^\gamma u$ and φ is an automorphism,
$0*u = bu=a^\gamma u$ and φ is an automorphism, ![]() $\varphi(a^\gamma u)=\varphi(0) *\varphi(u) = 0*u^\gamma f = au^\gamma f$. Since
$\varphi(a^\gamma u)=\varphi(0) *\varphi(u) = 0*u^\gamma f = au^\gamma f$. Since ![]() $a^\gamma u \in U$, we also have
$a^\gamma u \in U$, we also have  $\varphi(a^\gamma u) = a^{\gamma^2} u^\gamma f$. Therefore,
$\varphi(a^\gamma u) = a^{\gamma^2} u^\gamma f$. Therefore, ![]() $a^{\gamma^2} = a$. Since
$a^{\gamma^2} = a$. Since ![]() $U=U_a$ is the least subfield containing a, we see that
$U=U_a$ is the least subfield containing a, we see that ![]() $x^{\gamma^2} = x$ for every
$x^{\gamma^2} = x$ for every ![]() $x\in U$, by Lemma 4.1. Also
$x\in U$, by Lemma 4.1. Also ![]() $a\ne b=a^\gamma$, so
$a\ne b=a^\gamma$, so ![]() $\gamma\ne1$ and
$\gamma\ne1$ and ![]() $U = \mathbb F_{\gamma^2}$. The rest follows from Proposition 1.4.
$U = \mathbb F_{\gamma^2}$. The rest follows from Proposition 1.4.
Lemma 4.4. Let ![]() $Q = Q_{a,b}$, be a quadratic quasigroup over
$Q = Q_{a,b}$, be a quadratic quasigroup over ![]() $\mathbb F$, with a and b distinct non-squares. Let
$\mathbb F$, with a and b distinct non-squares. Let ![]() $\varphi \in \operatorname{Aut}(Q)$ be additive and let
$\varphi \in \operatorname{Aut}(Q)$ be additive and let ![]() $f=\varphi(1)$ be a non-square. Then there exists γ > 1 such that
$f=\varphi(1)$ be a non-square. Then there exists γ > 1 such that ![]() $b=a^\gamma$,
$b=a^\gamma$, ![]() $\gamma^2$ divides
$\gamma^2$ divides ![]() $|\mathbb F|$ and
$|\mathbb F|$ and ![]() $\mathbb F_{\gamma^2}$ carries a subquasigroup of Q that coincides with
$\mathbb F_{\gamma^2}$ carries a subquasigroup of Q that coincides with  $(\mathbb F_{\gamma^2},*_a)$.
$(\mathbb F_{\gamma^2},*_a)$.
Proof. The first step is to prove for each ![]() $i\geqslant 0$ that
$i\geqslant 0$ that
Now ![]() $\varphi(a)=\varphi(0*1)=\varphi(0)*\varphi(1)=0*f=bf$, so Condition (4.3) holds for i = 0. Also Condition (4.2) holds for i = 0 by the definition of f. Note that
$\varphi(a)=\varphi(0*1)=\varphi(0)*\varphi(1)=0*f=bf$, so Condition (4.3) holds for i = 0. Also Condition (4.2) holds for i = 0 by the definition of f. Note that ![]() $a^ib^i$ is a square and
$a^ib^i$ is a square and ![]() $a^ib^{i-1}$ is a non-square. So by induction on i, we find that
$a^ib^{i-1}$ is a non-square. So by induction on i, we find that
 \begin{gather*}
\varphi(a^{i}b^{i})=\varphi(0*a^ib^{i-1})=\varphi(0)*\varphi(a^ib^{i-1})=0*a^{i-1}b^if=a^{i}b^{i}f\ \text{and} \\
\varphi(a^{i+1}b^{i})=\varphi(0*a^ib^i)=\varphi(0)*\varphi(a^ib^i)=0*a^ib^if=a^{i}b^{i+1}f,
\end{gather*}
\begin{gather*}
\varphi(a^{i}b^{i})=\varphi(0*a^ib^{i-1})=\varphi(0)*\varphi(a^ib^{i-1})=0*a^{i-1}b^if=a^{i}b^{i}f\ \text{and} \\
\varphi(a^{i+1}b^{i})=\varphi(0*a^ib^i)=\varphi(0)*\varphi(a^ib^i)=0*a^ib^if=a^{i}b^{i+1}f,
\end{gather*}completing the proof of Conditions (4.2) and (4.3).
Denote by C the subfield of ![]() $\mathbb F$ generated by ab. By Lemma 4.1, each element of C may be expressed as a sum
$\mathbb F$ generated by ab. By Lemma 4.1, each element of C may be expressed as a sum ![]() $(ab)^{i_1}+\dots + (ab)^{i_k}$. Hence,
$(ab)^{i_1}+\dots + (ab)^{i_k}$. Hence, ![]() $\varphi(c) = cf$ for each
$\varphi(c) = cf$ for each ![]() $c\in C$, by Condition (4.2).
$c\in C$, by Condition (4.2).
Let us now assume that there exists ![]() $\zeta\in C$ such that
$\zeta\in C$ such that ![]() $\chi(\zeta) = -1$. In such a case, the non-squares of C coincide with the non-squares of
$\chi(\zeta) = -1$. In such a case, the non-squares of C coincide with the non-squares of ![]() $\mathbb F$ contained in C, and, as we shall prove, whenever
$\mathbb F$ contained in C, and, as we shall prove, whenever ![]() $x,y \in \mathbb F$ such that
$x,y \in \mathbb F$ such that ![]() $\chi(x) = \chi(y)$ and that
$\chi(x) = \chi(y)$ and that ![]() $\varphi(x) = yf$, then
$\varphi(x) = yf$, then
Let us assume that the hypothesis of Condition (4.4) is true. Our aim is to show that then ![]() $\varphi(axc) = bycf$ for each
$\varphi(axc) = bycf$ for each ![]() $c\in C$. The first step is a choice of
$c\in C$. The first step is a choice of ![]() $x^{\prime},y^{\prime}\in \mathbb F$. If x is a square, put
$x^{\prime},y^{\prime}\in \mathbb F$. If x is a square, put ![]() $(x^{\prime},y^{\prime})=(x,y)$. If x is a non-square, put
$(x^{\prime},y^{\prime})=(x,y)$. If x is a non-square, put ![]() $(x^{\prime},y^{\prime}) = (x\zeta,y\zeta)$, where ζ is as above. By the hypothesis of Condition (4.4),
$(x^{\prime},y^{\prime}) = (x\zeta,y\zeta)$, where ζ is as above. By the hypothesis of Condition (4.4), ![]() $\varphi(x^{\prime}s) = y^{\prime}sf$ for each square
$\varphi(x^{\prime}s) = y^{\prime}sf$ for each square ![]() $s\in C$. Since
$s\in C$. Since ![]() $x^{\prime}s$ and
$x^{\prime}s$ and ![]() $y^{\prime}s$ are squares,
$y^{\prime}s$ are squares, ![]() $\varphi(ax^{\prime}s)=\varphi(0*x^{\prime}s)=\varphi(0)*\varphi(x^{\prime}s)=0*y^{\prime}sf=by^{\prime}sf$ for each square
$\varphi(ax^{\prime}s)=\varphi(0*x^{\prime}s)=\varphi(0)*\varphi(x^{\prime}s)=0*y^{\prime}sf=by^{\prime}sf$ for each square ![]() $s\in C$. If
$s\in C$. If ![]() $t\in C$ is another square, then
$t\in C$ is another square, then ![]() $\varphi(ax^{\prime}(s+t))=by^{\prime}(s+t)f$ since φ is additive. Therefore,
$\varphi(ax^{\prime}(s+t))=by^{\prime}(s+t)f$ since φ is additive. Therefore, ![]() $\varphi(ax^{\prime}c) = by^{\prime}cf$ for each
$\varphi(ax^{\prime}c) = by^{\prime}cf$ for each ![]() $c\in C$, by Lemma 4.2. That finishes the proof of Condition (4.4) since
$c\in C$, by Lemma 4.2. That finishes the proof of Condition (4.4) since ![]() $\zeta \in C$.
$\zeta \in C$.
Assuming the existence of ζ, Condition (4.4) implies ![]() $\varphi(a^ic) = b^i c f$, for each
$\varphi(a^ic) = b^i c f$, for each ![]() $i \geqslant 0$ and
$i \geqslant 0$ and ![]() $c\in C$. Indeed, since we have proved that
$c\in C$. Indeed, since we have proved that ![]() $\varphi(c) = cf$ for each
$\varphi(c) = cf$ for each ![]() $c\in C$, the equality holds for i = 0. The induction step follows from Condition (4.4), by setting
$c\in C$, the equality holds for i = 0. The induction step follows from Condition (4.4), by setting ![]() $(x,y) = (a^i,b^i)$.
$(x,y) = (a^i,b^i)$.
We have shown that if C carries a non-square in ![]() $\mathbb F$, then
$\mathbb F$, then ![]() $\varphi(a^i) =b^if$ for every
$\varphi(a^i) =b^if$ for every ![]() $i \geqslant 0$. That allows us to draw the needed conclusions from Lemma 4.3. So, for the rest of the proof, we may assume that each element of C is a square in
$i \geqslant 0$. That allows us to draw the needed conclusions from Lemma 4.3. So, for the rest of the proof, we may assume that each element of C is a square in ![]() $\mathbb F$. In particular,
$\mathbb F$. In particular, ![]() $\chi(-1) = 1$.
$\chi(-1) = 1$.
Now ![]() $\varphi(a)=\varphi(0*1) =\varphi(0)*\varphi(1) = 0*f =bf$ and
$\varphi(a)=\varphi(0*1) =\varphi(0)*\varphi(1) = 0*f =bf$ and ![]() $\chi(a-1)=\chi(b-1)$, by Condition (1.2). Thus, the claim
$\chi(a-1)=\chi(b-1)$, by Condition (1.2). Thus, the claim
holds for i = 1. Let us now show that if ![]() $\varphi(a^j)=b^jf$ holds for each positive
$\varphi(a^j)=b^jf$ holds for each positive ![]() $j\leqslant i$, then
$j\leqslant i$, then ![]() $\chi(a^i-1)=\chi(b^i-1)$. Since
$\chi(a^i-1)=\chi(b^i-1)$. Since ![]() $\chi(a-1)=\chi(b-1)$, it suffices to show that
$\chi(a-1)=\chi(b-1)$, it suffices to show that ![]() $\chi(A)=\chi(B)$, where
$\chi(A)=\chi(B)$, where  $A=\sum_{j=0}^{i-1}a^j$ and
$A=\sum_{j=0}^{i-1}a^j$ and  $B=\sum_{j=0}^{i-1}b^j$. Note that
$B=\sum_{j=0}^{i-1}b^j$. Note that ![]() $\varphi(A) = Bf$. It follows that A = 0 if and only if B = 0, so we may assume that
$\varphi(A) = Bf$. It follows that A = 0 if and only if B = 0, so we may assume that ![]() $A\ne0$ and
$A\ne0$ and ![]() $B\ne0$. Suppose that A is a non-zero square, so that
$B\ne0$. Suppose that A is a non-zero square, so that ![]() $0*A=aA$. Since φ is an additive automorphism, we must have
$0*A=aA$. Since φ is an additive automorphism, we must have ![]() $0*fB=\varphi(aA)=fbB$. However, that is possible if and only if B is a square. Conversely, if B is a square, then
$0*fB=\varphi(aA)=fbB$. However, that is possible if and only if B is a square. Conversely, if B is a square, then ![]() $\varphi(0*A)=0*fB=fbB=\varphi(aA)$, implying that
$\varphi(0*A)=0*fB=fbB=\varphi(aA)$, implying that ![]() $0*A = aA$. Hence, A is a square in
$0*A = aA$. Hence, A is a square in ![]() $\mathbb F$ if and only if B is a square in
$\mathbb F$ if and only if B is a square in ![]() $\mathbb F$, and the same holds for
$\mathbb F$, and the same holds for ![]() $a^i-1$ and
$a^i-1$ and ![]() $b^i-1$.
$b^i-1$.
Thus, Condition (4.5) holds for all ![]() $i\geqslant 1$ if we can prove that its validity for a given
$i\geqslant 1$ if we can prove that its validity for a given ![]() $i\geqslant 1$ implies
$i\geqslant 1$ implies ![]() $\varphi(a^{i+1}) = b^{i+1}f$. For even i, we need only observe that
$\varphi(a^{i+1}) = b^{i+1}f$. For even i, we need only observe that ![]() $\varphi(a^{i+1})=\varphi(0*a^i)=\varphi(0)*\varphi(a^i)=0*b^if=b^{i+1}f$. So we may suppose that i is odd.
$\varphi(a^{i+1})=\varphi(0*a^i)=\varphi(0)*\varphi(a^i)=0*b^if=b^{i+1}f$. So we may suppose that i is odd.
Assume first that ![]() $a^i-1$ is a square. Then
$a^i-1$ is a square. Then
Since ![]() $\varphi(-a) =-bf$ and φ is additive, we have
$\varphi(-a) =-bf$ and φ is additive, we have ![]() $\varphi(a^{i+1})=b^{i+1}f$.
$\varphi(a^{i+1})=b^{i+1}f$.
Suppose now that ![]() $a^i-1$ is a non-square. Then
$a^i-1$ is a non-square. Then ![]() $b^i-1$ is a non-square too, and
$b^i-1$ is a non-square too, and ![]() $(b^i-1)(-a^i) = a^i - (ab)^i$ is a square. By the inductive assumption and Condition (4.2), we see that
$(b^i-1)(-a^i) = a^i - (ab)^i$ is a square. By the inductive assumption and Condition (4.2), we see that
is a non-square. Hence, by Condition (4.3),
 \begin{align*}
\varphi(a^{i+1})-a^ib^{i+1}f&=\varphi(a^{i+1} - a^{i+1}b^i)=\varphi(0*(a^i-(ab)^i)) =
0*(b^i -(ab)^i)f\\
&=b^{i+1}f - a^ib^{i+1}f.
\end{align*}
\begin{align*}
\varphi(a^{i+1})-a^ib^{i+1}f&=\varphi(a^{i+1} - a^{i+1}b^i)=\varphi(0*(a^i-(ab)^i)) =
0*(b^i -(ab)^i)f\\
&=b^{i+1}f - a^ib^{i+1}f.
\end{align*} Therefore, ![]() $\varphi(a^{i+1})=b^{i+1}f$, completing the proof of Condition (4.5). We see that Lemma 4.3 may be applied in this case too.
$\varphi(a^{i+1})=b^{i+1}f$, completing the proof of Condition (4.5). We see that Lemma 4.3 may be applied in this case too.
Proposition 4.5. Let ![]() $Q = Q_{a,b}$ be a non-affine quadratic quasigroup over
$Q = Q_{a,b}$ be a non-affine quadratic quasigroup over ![]() $\mathbb F$. Suppose that there exists
$\mathbb F$. Suppose that there exists ![]() $\varphi \in \operatorname{Aut}(Q)$ such that φ is additive and
$\varphi \in \operatorname{Aut}(Q)$ such that φ is additive and ![]() $\varphi(1)$ is a non-square. Then
$\varphi(1)$ is a non-square. Then ![]() $b = a^\gamma$, where
$b = a^\gamma$, where ![]() $\gamma^2$ divides
$\gamma^2$ divides ![]() $|\mathbb F|$ and γ > 1. The subfield U generated by a is equal to
$|\mathbb F|$ and γ > 1. The subfield U generated by a is equal to ![]() $\mathbb F_{\gamma^2}$ and forms a subquasigroup of Q such that
$\mathbb F_{\gamma^2}$ and forms a subquasigroup of Q such that  $(U,*) = (\mathbb F_{\gamma^2},*_a)$.
$(U,*) = (\mathbb F_{\gamma^2},*_a)$.
Proof. If a and b are non-squares, then the result follows from Lemma 4.4, so we assume that a and b are squares. It is then easy to show by induction that ![]() $\varphi(a^i) = b^i f$ for every
$\varphi(a^i) = b^i f$ for every ![]() $i \geqslant 1$, where
$i \geqslant 1$, where ![]() $f=\varphi(1)$. Indeed
$f=\varphi(1)$. Indeed ![]() $\varphi(a) = bf$ since
$\varphi(a) = bf$ since ![]() $0*1 =a $, while
$0*1 =a $, while ![]() $\varphi(a^{i+1})
= \varphi(0*a^i) = 0 * b^if = b^{i+1}f$ yields the induction step. By Lemma 4.3, U is a subquasigroup,
$\varphi(a^{i+1})
= \varphi(0*a^i) = 0 * b^if = b^{i+1}f$ yields the induction step. By Lemma 4.3, U is a subquasigroup, ![]() $b =a^\gamma$ for γ > 1 such that
$b =a^\gamma$ for γ > 1 such that  $\gamma^2 \bigm| |\mathbb F|$, and the statement is true if U contains an element that is a non-square in
$\gamma^2 \bigm| |\mathbb F|$, and the statement is true if U contains an element that is a non-square in ![]() $\mathbb F$. Thus, for the rest of the proof, it will be assumed that each element of U is a square in
$\mathbb F$. Thus, for the rest of the proof, it will be assumed that each element of U is a square in ![]() $\mathbb F$. Let us also stipulate that γ > 1 is the least possible.
$\mathbb F$. Let us also stipulate that γ > 1 is the least possible.
The next step is to show that if ![]() $\chi(\varphi(f))=1$, then
$\chi(\varphi(f))=1$, then ![]() $\varphi(u^\gamma f) = u \varphi(f)$, while for
$\varphi(u^\gamma f) = u \varphi(f)$, while for ![]() $\chi(\varphi(f))=-1$ we have
$\chi(\varphi(f))=-1$ we have ![]() $\varphi(uf) = u \varphi(f)$, for each
$\varphi(uf) = u \varphi(f)$, for each ![]() $u \in U$.
$u \in U$.
We first assume ![]() $\chi(\varphi(f)) = 1$ and employ induction to prove that
$\chi(\varphi(f)) = 1$ and employ induction to prove that ![]() $\varphi(b^if) = a^i\varphi(f)$ for each
$\varphi(b^if) = a^i\varphi(f)$ for each ![]() $i\geqslant 0$. The case i = 0 is trivial, and
$i\geqslant 0$. The case i = 0 is trivial, and ![]() $\varphi(b^{i+1}f) = \varphi(0*b^if) = 0*a^i\varphi(f) = a^{i+1}\varphi(f)$ completes the induction. Each
$\varphi(b^{i+1}f) = \varphi(0*b^if) = 0*a^i\varphi(f) = a^{i+1}\varphi(f)$ completes the induction. Each ![]() $u\in U$ may be expressed as
$u\in U$ may be expressed as ![]() $\sum a^{i_j}$, by Lemma 4.1. In such a case,
$\sum a^{i_j}$, by Lemma 4.1. In such a case, ![]() $u^\gamma = \sum b^{i_j}$ and
$u^\gamma = \sum b^{i_j}$ and ![]() $\varphi(u^\gamma f) = u\varphi(f)$, by the additivity of φ.
$\varphi(u^\gamma f) = u\varphi(f)$, by the additivity of φ.
Assume now that ![]() $\chi(\varphi(f)) = -1$. Since b is the image of a under the field automorphism
$\chi(\varphi(f)) = -1$. Since b is the image of a under the field automorphism ![]() $x\mapsto x^\gamma$, we have
$x\mapsto x^\gamma$, we have ![]() $a = b^{\gamma'}$, where
$a = b^{\gamma'}$, where ![]() $x\mapsto x^{\gamma'}$ is the inverse automorphism. Thus, each
$x\mapsto x^{\gamma'}$ is the inverse automorphism. Thus, each ![]() $u\in U$ may be expressed as
$u\in U$ may be expressed as ![]() $\sum b^{i_j}$, by Lemma 4.1. Also,
$\sum b^{i_j}$, by Lemma 4.1. Also, ![]() $\varphi(b^if) = b^i\varphi(f)$ for each
$\varphi(b^if) = b^i\varphi(f)$ for each ![]() $i\geqslant 0$ by induction, since
$i\geqslant 0$ by induction, since ![]() $\varphi(b^{i+1}f) = \varphi(0*b^if) =0 * b^i\varphi(f) = b^{i+1}\varphi(f)$. Therefore,
$\varphi(b^{i+1}f) = \varphi(0*b^if) =0 * b^i\varphi(f) = b^{i+1}\varphi(f)$. Therefore, ![]() $\varphi(uf) = u\varphi(f)$ for each
$\varphi(uf) = u\varphi(f)$ for each ![]() $u \in U$, as claimed.
$u \in U$, as claimed.
The automorphism φ may be replaced by its composition with the affine isomorphism ![]() $x\mapsto cx$, where c is a square. Hence, f may be equal to any non-square in
$x\mapsto cx$, where c is a square. Hence, f may be equal to any non-square in ![]() $\mathbb F$. By Lemma 4.2, we may choose f in such a way that
$\mathbb F$. By Lemma 4.2, we may choose f in such a way that ![]() $1+f$ is a square. Then
$1+f$ is a square. Then
 \begin{align}
a^\gamma f + \varphi(af)& =\varphi(a+af)=\varphi(0*(1+f)) \\ & =0*\varphi(1+f)
\in \{af + a\varphi(f),
\, a^\gamma f + a^\gamma \varphi(f)\},
\end{align}
\begin{align}
a^\gamma f + \varphi(af)& =\varphi(a+af)=\varphi(0*(1+f)) \\ & =0*\varphi(1+f)
\in \{af + a\varphi(f),
\, a^\gamma f + a^\gamma \varphi(f)\},
\end{align} by Condition (1.1). If ![]() $\varphi(f)$ is a non-square, then
$\varphi(f)$ is a non-square, then ![]() $\varphi(af) = a\varphi(f)$, by the results above. This contradicts Condition (4.6) since
$\varphi(af) = a\varphi(f)$, by the results above. This contradicts Condition (4.6) since ![]() $a^\gamma \ne a$. Hence,
$a^\gamma \ne a$. Hence, ![]() $\varphi(f)$ is a square and
$\varphi(f)$ is a square and ![]() $\varphi(af) = a^{1/\gamma} \varphi(f)$. Suppose first that
$\varphi(af) = a^{1/\gamma} \varphi(f)$. Suppose first that
and choose ![]() $d\in \mathbb F$ such that
$d\in \mathbb F$ such that
 \begin{equation*} d^\gamma = \frac{a^\gamma - a}{a-a^{1/\gamma}}.\end{equation*}
\begin{equation*} d^\gamma = \frac{a^\gamma - a}{a-a^{1/\gamma}}.\end{equation*} Then ![]() $\varphi(f) = d^\gamma f$. Because
$\varphi(f) = d^\gamma f$. Because ![]() $d\in U$, we also have
$d\in U$, we also have ![]() $\varphi(d) = d^\gamma f$, by Lemma 4.3. Thus, d = f. This is a contradiction since d is a square and f is a non-square. Therefore,
$\varphi(d) = d^\gamma f$, by Lemma 4.3. Thus, d = f. This is a contradiction since d is a square and f is a non-square. Therefore, ![]() $a^{1/\gamma}\varphi(f) =a^\gamma \varphi(f)$, and
$a^{1/\gamma}\varphi(f) =a^\gamma \varphi(f)$, and ![]() $a^{\gamma^2} =a$. Hence,
$a^{\gamma^2} =a$. Hence, ![]() $|U|$ divides γ 2 and admits a non-trivial involutory automorphism
$|U|$ divides γ 2 and admits a non-trivial involutory automorphism ![]() $x\mapsto x^\gamma$. Since γ has been chosen to be the least possible, γ is a proper divisor of
$x\mapsto x^\gamma$. Since γ has been chosen to be the least possible, γ is a proper divisor of ![]() $|U|$. Thus,
$|U|$. Thus, ![]() $|U| = \gamma^2$.
$|U| = \gamma^2$.
Lemma 4.6. Let ![]() $Q_{a,b}$ be a 2-generated quadratic quasigroup over
$Q_{a,b}$ be a 2-generated quadratic quasigroup over ![]() $\mathbb F$. Then at least one of the quasigroups
$\mathbb F$. Then at least one of the quasigroups ![]() $Q_{a,b}$ and
$Q_{a,b}$ and ![]() $Q_{b,a}$ is generated by
$Q_{b,a}$ is generated by ![]() $\{0,1\}$.
$\{0,1\}$.
Proof. Put ![]() $Q=Q_{a,b}$. Since
$Q=Q_{a,b}$. Since ![]() $\operatorname{Aut}(Q)$ is transitive, there exists
$\operatorname{Aut}(Q)$ is transitive, there exists ![]() $u\in Q$ such that
$u\in Q$ such that ![]() $\{0,u\}$ generates Q. If u is a square, then Q is generated by
$\{0,u\}$ generates Q. If u is a square, then Q is generated by ![]() $\{0,1\}$ since
$\{0,1\}$ since ![]() $x\mapsto ux$ belongs to
$x\mapsto ux$ belongs to ![]() $\operatorname{Aut}(Q)$. Assume that u is a non-square. Then
$\operatorname{Aut}(Q)$. Assume that u is a non-square. Then ![]() $x\mapsto u^{-1} x$ is an isomorphism
$x\mapsto u^{-1} x$ is an isomorphism ![]() $Q_{a,b}\cong Q_{b,a}$, by Proposition 2.1(iv), and this isomorphism sends
$Q_{a,b}\cong Q_{b,a}$, by Proposition 2.1(iv), and this isomorphism sends ![]() $\{0,u\}$ to
$\{0,u\}$ to ![]() $\{0,1\}$.
$\{0,1\}$.
Theorem 4.7. Let ![]() $Q=Q_{a,b}$ be a 2-generated quadratic quasigroup over
$Q=Q_{a,b}$ be a 2-generated quadratic quasigroup over ![]() $\mathbb F$. Then
$\mathbb F$. Then ![]() $G=\operatorname{Aut}(Q)$ is 2-transitive if and only if a = b or
$G=\operatorname{Aut}(Q)$ is 2-transitive if and only if a = b or  $Q=(\mathbb F_{\gamma^2},*_a)$.
$Q=(\mathbb F_{\gamma^2},*_a)$.
In the former case, G consists of all mappings ![]() $x\mapsto \lambda x+\mu$, where
$x\mapsto \lambda x+\mu$, where ![]() $\lambda \in \mathbb F^*$ and
$\lambda \in \mathbb F^*$ and ![]() $\mu \in \mathbb F$. In the latter case, G consists of mappings
$\mu \in \mathbb F$. In the latter case, G consists of mappings ![]() $x\mapsto \lambda x+\mu$ and mappings
$x\mapsto \lambda x+\mu$ and mappings ![]() $x\mapsto \lambda^{\prime}
x^\gamma + \mu$, where
$x\mapsto \lambda^{\prime}
x^\gamma + \mu$, where ![]() $\lambda,\lambda^{\prime},
\mu \in \mathbb F$,
$\lambda,\lambda^{\prime},
\mu \in \mathbb F$, ![]() $\chi(\lambda)=1$ and
$\chi(\lambda)=1$ and ![]() $\chi(\lambda^{\prime}) = -1$.
$\chi(\lambda^{\prime}) = -1$.
If G is not ![]() $2$-transitive, then it consists of all mappings
$2$-transitive, then it consists of all mappings ![]() $x\mapsto \lambda x + \mu$, where
$x\mapsto \lambda x + \mu$, where ![]() $\lambda,\mu \in \mathbb F$ and
$\lambda,\mu \in \mathbb F$ and ![]() $\chi(\lambda) = 1$.
$\chi(\lambda) = 1$.
Proof. By Proposition 2.1, G contains all mappings ![]() $x\mapsto \lambda x + \mu$, where
$x\mapsto \lambda x + \mu$, where ![]() $\lambda \in \mathbb F^*$ is a square. Suppose first that G is 2-transitive. Then G is sharply 2-transitive since an automorphism that fixes generators pointwise has to be the identity mapping. The mappings
$\lambda \in \mathbb F^*$ is a square. Suppose first that G is 2-transitive. Then G is sharply 2-transitive since an automorphism that fixes generators pointwise has to be the identity mapping. The mappings ![]() $x\mapsto x+\mu$ thus form a normal subgroup of G, and that makes each
$x\mapsto x+\mu$ thus form a normal subgroup of G, and that makes each ![]() $\varphi \in G_0$ additive (where G 0 is the stabilizer of 0 in G). Proposition 4.5 hence confirms that G may be 2-transitive only in the cases described above. All mappings mentioned so far are automorphisms of Q, and they form a 2-transitive group. No other automorphism of Q may thus exist.
$\varphi \in G_0$ additive (where G 0 is the stabilizer of 0 in G). Proposition 4.5 hence confirms that G may be 2-transitive only in the cases described above. All mappings mentioned so far are automorphisms of Q, and they form a 2-transitive group. No other automorphism of Q may thus exist.
Let us now turn to the case when G is not 2-transitive. Let Q be generated by ![]() $\{0,u\}$. Then
$\{0,u\}$. Then ![]() $\chi(u) = \chi(\varphi(u))$ for each
$\chi(u) = \chi(\varphi(u))$ for each ![]() $\varphi \in G_0$ since otherwise G is 2-transitive. For each
$\varphi \in G_0$ since otherwise G is 2-transitive. For each ![]() $\varphi \in G_0$, there thus exists a square
$\varphi \in G_0$, there thus exists a square ![]() $\lambda \in
\mathbb F^*$ such that
$\lambda \in
\mathbb F^*$ such that ![]() $\varphi(u) = \lambda u$. Since φ and
$\varphi(u) = \lambda u$. Since φ and ![]() $x\mapsto \lambda x$ agree on a set of generators, they agree everywhere. Nothing else is needed.
$x\mapsto \lambda x$ agree on a set of generators, they agree everywhere. Nothing else is needed.
Theorem 4.8. Let ![]() $Q=Q_{a,b}$ be a 2-generated quadratic quasigroup over
$Q=Q_{a,b}$ be a 2-generated quadratic quasigroup over ![]() $\mathbb F$. Then
$\mathbb F$. Then ![]() $Q \cong Q_{c,d}$ if and only if there exists
$Q \cong Q_{c,d}$ if and only if there exists ![]() $\alpha\in \operatorname{Aut}(\mathbb F)$ such that
$\alpha\in \operatorname{Aut}(\mathbb F)$ such that ![]() $\{c,d\} = \{\alpha(a),\alpha(b)\}$.
$\{c,d\} = \{\alpha(a),\alpha(b)\}$.
Proof. By Proposition 2.1, only the direct implication needs to be proved. Fix an isomorphism ![]() $\psi\colon Q\mapsto Q_{c,d}$ and put
$\psi\colon Q\mapsto Q_{c,d}$ and put ![]() $G=\operatorname{Aut}(Q)$. The group G is 2-transitive if and only if
$G=\operatorname{Aut}(Q)$. The group G is 2-transitive if and only if ![]() $\operatorname{Aut}(Q_{c,d})$ is 2-transitive. If a = b, then c = d since this is the only 2-transitive case in which G 0 is abelian, by Theorem 4.7. Hence, Theorem 4.7 implies that G is equal to
$\operatorname{Aut}(Q_{c,d})$ is 2-transitive. If a = b, then c = d since this is the only 2-transitive case in which G 0 is abelian, by Theorem 4.7. Hence, Theorem 4.7 implies that G is equal to ![]() $\operatorname{Aut}(Q_{c,d})$ in all cases. Therefore, ψ normalizes G, and hence ψ also normalizes the group of translations
$\operatorname{Aut}(Q_{c,d})$ in all cases. Therefore, ψ normalizes G, and hence ψ also normalizes the group of translations ![]() $x\mapsto x+\mu$. Since G is transitive,
$x\mapsto x+\mu$. Since G is transitive, ![]() $\psi(0) = 0$ may be assumed. The normalizing property means that ψ is additive and normalizes G 0.
$\psi(0) = 0$ may be assumed. The normalizing property means that ψ is additive and normalizes G 0.
By Lemma 4.6, it may be assumed that Q is generated by 0 and 1. Then 0 and ![]() $\psi(1)$ generate
$\psi(1)$ generate ![]() $Q_{c,d}$. After a possible switch of c and d, we may thus assume that
$Q_{c,d}$. After a possible switch of c and d, we may thus assume that ![]() $\psi(1) = 1$ as well, by Proposition 2.1(iii), (iv).
$\psi(1) = 1$ as well, by Proposition 2.1(iii), (iv).
Denote by σs the multiplication ![]() $x\mapsto sx$, where
$x\mapsto sx$, where ![]() $s\in \mathbb F^*$. If
$s\in \mathbb F^*$. If ![]() $\sigma_s\in G_0$, then
$\sigma_s\in G_0$, then ![]() $\psi \sigma_s \psi^{-1} = \sigma_t$ for some
$\psi \sigma_s \psi^{-1} = \sigma_t$ for some ![]() $t\in \mathbb F^*$ since ψ normalizes G 0. Since
$t\in \mathbb F^*$ since ψ normalizes G 0. Since ![]() $\psi(1) = 1$, we must have
$\psi(1) = 1$, we must have ![]() $t=\psi(s)$. Hence,
$t=\psi(s)$. Hence, ![]() $\psi(sy)=\psi\sigma_s(y) = \sigma_{t}\psi(y)=\psi(s)\psi(y)$ for all
$\psi(sy)=\psi\sigma_s(y) = \sigma_{t}\psi(y)=\psi(s)\psi(y)$ for all ![]() $y\in\mathbb F$, whenever
$y\in\mathbb F$, whenever ![]() $\sigma_s \in G_0$. This shows that
$\sigma_s \in G_0$. This shows that ![]() $\psi\in \operatorname{Aut}(\mathbb F)$ if a = b.
$\psi\in \operatorname{Aut}(\mathbb F)$ if a = b.
Suppose that ![]() $a\ne b$. We shall show that
$a\ne b$. We shall show that ![]() $\psi\in \operatorname{Aut}(\mathbb F)$ in this case too. Indeed, if
$\psi\in \operatorname{Aut}(\mathbb F)$ in this case too. Indeed, if ![]() $x\in \mathbb F$ is a non-square, then x may be expressed as u + v, where both u and v are squares, by Lemma 4.2. In such a case,
$x\in \mathbb F$ is a non-square, then x may be expressed as u + v, where both u and v are squares, by Lemma 4.2. In such a case, ![]() $\psi(xy) = \psi(uy + vy) = (\psi(u)+\psi(v))\psi(y) = \psi(x)\psi(y)$ for all
$\psi(xy) = \psi(uy + vy) = (\psi(u)+\psi(v))\psi(y) = \psi(x)\psi(y)$ for all ![]() $y\in\mathbb F$.
$y\in\mathbb F$.
To finish, note that in ![]() $Q_{c,d}$ both
$Q_{c,d}$ both ![]() $c=0*1 = \psi(0)*\psi(1) =\psi(a)$ and
$c=0*1 = \psi(0)*\psi(1) =\psi(a)$ and ![]() $\psi(b)\psi(\zeta) = \psi(b\zeta) = \psi(0*\zeta) = 0*\psi(\zeta)= d\psi(\zeta)$ hold, where ζ is any non-square. Hence,
$\psi(b)\psi(\zeta) = \psi(b\zeta) = \psi(0*\zeta) = 0*\psi(\zeta)= d\psi(\zeta)$ hold, where ζ is any non-square. Hence, ![]() $c = \psi(a)$ and
$c = \psi(a)$ and ![]() $d=\psi(b)$.
$d=\psi(b)$.
5. Subfields and subquasigroups
In this section, we examine the structure of minimal subquasigroups and 2-generated subquasigroups of quadratic quasigroups. Note that in Steiner quasigroups, every pair of elements generates a (minimal) subquasigroup of order 3, by definition. As this case is trivial, we may for convenience exclude certain Steiner quasigroups from our discussions in this section.
Let us start with an easy general fact:
Lemma 5.1. Let Q be a finite quasigroup and let α be an automorphism of Q. Suppose that S is a subquasigroup of Q that is generated by a set X. Then ![]() $\alpha(S) = S$ if and only if
$\alpha(S) = S$ if and only if ![]() $\alpha(X)\subseteq S$.
$\alpha(X)\subseteq S$.
Proof. If ![]() $\alpha(S) = S$, then
$\alpha(S) = S$, then ![]() $\alpha(X)\subseteq S$. Conversely, assume
$\alpha(X)\subseteq S$. Conversely, assume ![]() $\alpha(X)\subseteq S$, and denote by
$\alpha(X)\subseteq S$, and denote by ![]() $S^{\prime}$ the subquasigroup generated by
$S^{\prime}$ the subquasigroup generated by ![]() $\alpha(X)$. We have
$\alpha(X)$. We have ![]() $\alpha(X)\subseteq S^{\prime}\cap S$, so
$\alpha(X)\subseteq S^{\prime}\cap S$, so ![]() $S^{\prime} \subseteq S$. However, α is an isomorphism from S to
$S^{\prime} \subseteq S$. However, α is an isomorphism from S to ![]() $S^{\prime}$ so
$S^{\prime}$ so ![]() $|S^{\prime}|=|S|$, which means that
$|S^{\prime}|=|S|$, which means that ![]() $\alpha(S)=S^{\prime} = S$.
$\alpha(S)=S^{\prime} = S$.
Lemma 5.2. Let ![]() $Q=Q_{a,b}$ be a quadratic quasigroup over
$Q=Q_{a,b}$ be a quadratic quasigroup over ![]() $\mathbb F$. The set of all
$\mathbb F$. The set of all ![]() $\sum a^{i_k}b^{j_k}$, where
$\sum a^{i_k}b^{j_k}$, where ![]() $1\leqslant k \leqslant r$, with
$1\leqslant k \leqslant r$, with ![]() $i_k \geqslant 0$,
$i_k \geqslant 0$, ![]() $j_k \geqslant 0$ and
$j_k \geqslant 0$ and ![]() $r\geqslant 0$, coincides with the least subfield of
$r\geqslant 0$, coincides with the least subfield of ![]() $\mathbb F$ that contains
$\mathbb F$ that contains ![]() $\{a,b\}$. This subfield is a subquasigroup of Q.
$\{a,b\}$. This subfield is a subquasigroup of Q.
Proof. The set is closed under sums and products, and hence a subfield. By Definition (1.1), it is closed under ![]() $*$ as well.
$*$ as well.
Lemma 5.3. Let Q be a quadratic quasigroup over ![]() $\mathbb F$ that is not a Netto quasigroup. Let S is a minimal subquasigroup of Q, and
$\mathbb F$ that is not a Netto quasigroup. Let S is a minimal subquasigroup of Q, and ![]() $\{0,1\}\subseteq S$, then S is a subfield of
$\{0,1\}\subseteq S$, then S is a subfield of ![]() $\mathbb F$ and
$\mathbb F$ and ![]() $a\in S$. If S contains a non-square, then
$a\in S$. If S contains a non-square, then ![]() $b\in S$, and S is equal to the least subfield of
$b\in S$, and S is equal to the least subfield of ![]() $\mathbb F$ that contains a and b. If S is composed of squares only, then S coincides with the least subfield of
$\mathbb F$ that contains a and b. If S is composed of squares only, then S coincides with the least subfield of ![]() $\mathbb F$ that contains a.
$\mathbb F$ that contains a.
Proof. By Proposition 3.4 and Lemma 2.7, S is a subspace of ![]() $\mathbb F$. Moreover, if Q is affine Steiner, then S is equal to
$\mathbb F$. Moreover, if Q is affine Steiner, then S is equal to ![]() $\{0,1,-1\}$ and is a subfield that contains
$\{0,1,-1\}$ and is a subfield that contains ![]() $a=b=-1$. For the rest of the proof, it thus may be assumed that Q is not a Steiner quasigroup.
$a=b=-1$. For the rest of the proof, it thus may be assumed that Q is not a Steiner quasigroup.
Put ![]() $S_0 = \{\sum x_i:x_i\in S$ and
$S_0 = \{\sum x_i:x_i\in S$ and ![]() $\chi(x_i) \geqslant 0 \}$ and note that
$\chi(x_i) \geqslant 0 \}$ and note that ![]() $S_0\subseteq S$. If
$S_0\subseteq S$. If ![]() $s\in S$ is a non-zero square, then the automorphism
$s\in S$ is a non-zero square, then the automorphism ![]() $x\mapsto sx$ sends 0 to 0 and 1 to
$x\mapsto sx$ sends 0 to 0 and 1 to ![]() $s\in S$. Thus, 0 and s generate S, by Lemma 5.1. Hence, sS = S and
$s\in S$. Thus, 0 and s generate S, by Lemma 5.1. Hence, sS = S and ![]() $sS_0\subseteq S_0$. Since S 0 is a subspace,
$sS_0\subseteq S_0$. Since S 0 is a subspace, ![]() $S_0 S_0\subseteq S_0$, and that implies that S 0 is a subfield of
$S_0 S_0\subseteq S_0$, and that implies that S 0 is a subfield of ![]() $\mathbb F$. Furthermore, S is a vector space over S 0, since
$\mathbb F$. Furthermore, S is a vector space over S 0, since ![]() $x_iS \subseteq S$ yields
$x_iS \subseteq S$ yields ![]() $(\sum x_i)S
\subseteq S$.
$(\sum x_i)S
\subseteq S$.
If ![]() $\{a,b\}\subseteq S_0$, then
$\{a,b\}\subseteq S_0$, then ![]() $S=S_0$, by Lemma 5.2. Note that
$S=S_0$, by Lemma 5.2. Note that ![]() $a=0*1$ always belongs to S.
$a=0*1$ always belongs to S.
Let a be a square. Then ![]() $a^i\in S_0$ for each
$a^i\in S_0$ for each ![]() $i\geqslant 0$ since
$i\geqslant 0$ since ![]() $0*a^i= a^{i+1}$. Hence,
$0*a^i= a^{i+1}$. Hence, ![]() $S_0\supseteq S_a$ by Lemma 4.1, where Sa is the least subfield of
$S_0\supseteq S_a$ by Lemma 4.1, where Sa is the least subfield of ![]() $\mathbb F$ that contains a. If S 0 consists only of squares, then Sa is a subquasigroup, and
$\mathbb F$ that contains a. If S 0 consists only of squares, then Sa is a subquasigroup, and ![]() $S_a=S_0=S$. Suppose that S 0 contains a non-square, say ζ. To show that
$S_a=S_0=S$. Suppose that S 0 contains a non-square, say ζ. To show that ![]() $b\in S_0$, it suffices to show that
$b\in S_0$, it suffices to show that ![]() $b\in S$, since b is a square. Now,
$b\in S$, since b is a square. Now, ![]() $b\zeta = 0
* \zeta \in S$. Hence,
$b\zeta = 0
* \zeta \in S$. Hence, ![]() $b=\zeta^{-1} (\zeta b)\in S$, since
$b=\zeta^{-1} (\zeta b)\in S$, since ![]() $\zeta^{-1} \in S_0$ and S 0 acts on S.
$\zeta^{-1} \in S_0$ and S 0 acts on S.
For the remainder of the proof, let a and b be non-squares. If S 0 contains a non-square, say ζ, then ![]() $b\zeta = 0*\zeta \in S_0$. Therefore,
$b\zeta = 0*\zeta \in S_0$. Therefore, ![]() $b = \zeta^{-1}(\zeta b) \in S_0$. Since
$b = \zeta^{-1}(\zeta b) \in S_0$. Since ![]() $a\in S$,
$a\in S$, ![]() $0*a = ab \in S_0$, and hence
$0*a = ab \in S_0$, and hence ![]() $a = b^{-1} (ab) \in S_0$. Thus, if S 0 contains a non-square, then
$a = b^{-1} (ab) \in S_0$. Thus, if S 0 contains a non-square, then ![]() $\{a,b\}\subseteq S_0=S$, and S contains the subfield generated by a and b. In such a case, the subfield is equal to S, since the subfield is a subquasigroup containing a and b, by Lemma 5.2.
$\{a,b\}\subseteq S_0=S$, and S contains the subfield generated by a and b. In such a case, the subfield is equal to S, since the subfield is a subquasigroup containing a and b, by Lemma 5.2.
What remains is the case in which S 0 contains only squares, i.e. the squares of S form a subfield. We shall show that this may be always brought to a contradiction. Consider distinct ![]() $s,t\in S_0$. If
$s,t\in S_0$. If ![]() $s*t = s+a(t-s)$ is a square, i.e.
$s*t = s+a(t-s)$ is a square, i.e. ![]() $s*t\in S_0$, then
$s*t\in S_0$, then ![]() $a(t-s) = s*t -s$ is a square too, a contradiction. Hence,
$a(t-s) = s*t -s$ is a square too, a contradiction. Hence, ![]() $s*t \in N_1 = S\setminus S_0$. If
$s*t \in N_1 = S\setminus S_0$. If ![]() $s\in S_0\setminus\{0\}$, then
$s\in S_0\setminus\{0\}$, then ![]() $0*s = as \in N_1$. If
$0*s = as \in N_1$. If ![]() $n\in N_1$, then
$n\in N_1$, then ![]() $0*n = bn \in S_0$. Therefore,
$0*n = bn \in S_0$. Therefore, ![]() $|S_0|=|N_1|+1$. Consider now the multiplication table of
$|S_0|=|N_1|+1$. Consider now the multiplication table of ![]() $(S,*)$. Note that S is a disjoint union of S 0 and N 1. The subtable
$(S,*)$. Note that S is a disjoint union of S 0 and N 1. The subtable ![]() $S_0\times S_0$ has elements of S 0 on the diagonal, and the rest is occupied by elements of N 1. Therefore, all entries in subtables
$S_0\times S_0$ has elements of S 0 on the diagonal, and the rest is occupied by elements of N 1. Therefore, all entries in subtables ![]() $S_0\times N_1$ and
$S_0\times N_1$ and ![]() $N_1\times S_0$ belong to S 0. Therefore, all entries in
$N_1\times S_0$ belong to S 0. Therefore, all entries in ![]() $N_1\times N_1$ are from N 1, and that makes N 1 a subquasigroup. Since S is a minimal subquasigroup and
$N_1\times N_1$ are from N 1, and that makes N 1 a subquasigroup. Since S is a minimal subquasigroup and ![]() $N_1\ne S$, the only possibility is that
$N_1\ne S$, the only possibility is that ![]() $N_1=\{a\}$ and
$N_1=\{a\}$ and ![]() $S_0 = \{0,1\}$. Since S is a subspace,
$S_0 = \{0,1\}$. Since S is a subspace, ![]() $\operatorname{char}(\mathbb F) = 3$,
$\operatorname{char}(\mathbb F) = 3$, ![]() $a=-1$ and
$a=-1$ and ![]() $ab = 0*a = 0*-1 = 1$. That implies
$ab = 0*a = 0*-1 = 1$. That implies ![]() $b=-1$. By Lemma 2.7, this means that Q is a Steiner quasigroup, contrary to our assumptions.
$b=-1$. By Lemma 2.7, this means that Q is a Steiner quasigroup, contrary to our assumptions.
Theorem 5.4. Let ![]() $Q =Q_{a,b}$ be a quadratic quasigroup over
$Q =Q_{a,b}$ be a quadratic quasigroup over ![]() $\mathbb F$ that is not a Netto quasigroup. Let
$\mathbb F$ that is not a Netto quasigroup. Let ![]() $\mathbb K$,
$\mathbb K$, ![]() $\mathbb K_0$ and
$\mathbb K_0$ and ![]() $\mathbb K_1$ be the subfields generated by
$\mathbb K_1$ be the subfields generated by ![]() $\{a,b\}$,
$\{a,b\}$, ![]() $\{a\}$ and
$\{a\}$ and ![]() $\{b\}$, respectively. Suppose that each subquasigroup of Q that is generated by two distinct elements is minimal. There are two possibilities:
$\{b\}$, respectively. Suppose that each subquasigroup of Q that is generated by two distinct elements is minimal. There are two possibilities:
(i)
 $\mathbb K$ contains an element that is a non-square in
$\mathbb K$ contains an element that is a non-square in  $\mathbb F$, and
$\mathbb F$, and  $\mathbb K = \mathbb K_0=\mathbb K_1$. The minimal subquasigroups of Q are exactly the sets
$\mathbb K = \mathbb K_0=\mathbb K_1$. The minimal subquasigroups of Q are exactly the sets  $\lambda \mathbb K + \mu$, where
$\lambda \mathbb K + \mu$, where  $\lambda \in \mathbb F^*$ and
$\lambda \in \mathbb F^*$ and  $\mu \in \mathbb F$.
$\mu \in \mathbb F$.(ii) All elements of
 $\mathbb K_i$,
$\mathbb K_i$,  $i\in \{0,1\}$, are squares in
$i\in \{0,1\}$, are squares in  $\mathbb F$. If
$\mathbb F$. If  $\zeta \in \mathbb F$ is a non-square, then the minimal subquasigroups of Q are exactly the sets
$\zeta \in \mathbb F$ is a non-square, then the minimal subquasigroups of Q are exactly the sets  $\lambda \zeta^i\mathbb K_i + \mu$, where
$\lambda \zeta^i\mathbb K_i + \mu$, where  $\lambda \in \mathbb F^*$ is a square, and
$\lambda \in \mathbb F^*$ is a square, and  $\mu\in \mathbb F$.
$\mu\in \mathbb F$.
Proof. Denote by K the minimal subquasigroup generated by 0 and 1. Lemma 5.3 implies that if K contains a non-square, then ![]() $K = \mathbb K= \mathbb K_0=\mathbb K_1$. The other possibility is that K consists of squares only. Then
$K = \mathbb K= \mathbb K_0=\mathbb K_1$. The other possibility is that K consists of squares only. Then ![]() $K = \mathbb K_0$.
$K = \mathbb K_0$.
Suppose that ![]() $\lambda\in \mathbb F^*$ and
$\lambda\in \mathbb F^*$ and ![]() $\mu \in \mathbb F$. If λ is a square, then
$\mu \in \mathbb F$. If λ is a square, then ![]() $x\mapsto \lambda x + \mu$ is an automorphism of Q, by Proposition 2.1(iii). That makes
$x\mapsto \lambda x + \mu$ is an automorphism of Q, by Proposition 2.1(iii). That makes ![]() $\lambda K + \mu$ a minimal subquasigroup of Q. If K contains a non-square ζ, then
$\lambda K + \mu$ a minimal subquasigroup of Q. If K contains a non-square ζ, then ![]() $\zeta K = K$ and
$\zeta K = K$ and ![]() $\lambda K +\mu =\lambda\zeta K +\mu$.
$\lambda K +\mu =\lambda\zeta K +\mu$.
Let S be a minimal subquasigroup of Q that contains 0. By Proposition 2.1(ii), no other subquasigroups need to be considered.
Suppose there exists ![]() $s\in S$ and
$s\in S$ and ![]() $\xi\in K$ such that
$\xi\in K$ such that ![]() $\chi(s)=\chi(\xi)\ne0$. Let
$\chi(s)=\chi(\xi)\ne0$. Let ![]() $\lambda=s/\xi$ and note that
$\lambda=s/\xi$ and note that ![]() $x\mapsto \lambda x$ is an automorphism of Q that maps
$x\mapsto \lambda x$ is an automorphism of Q that maps ![]() $\{0,\xi\}$ to
$\{0,\xi\}$ to ![]() $\{0,s\}$. By minimality, the former set generates K, while the latter set generates S. Therefore
$\{0,s\}$. By minimality, the former set generates K, while the latter set generates S. Therefore ![]() $\lambda K=S$. Such a λ always exists if K contains a non-square.
$\lambda K=S$. Such a λ always exists if K contains a non-square.
Suppose that ![]() $K=\mathbb K_0$ consists of squares only. If S contains a non-zero square, then, as we have proved,
$K=\mathbb K_0$ consists of squares only. If S contains a non-zero square, then, as we have proved, ![]() $S= \lambda \mathbb K_0$, where λ is a square. In such a case, all elements of S are squares. What remains to be characterized are those minimal subquasigroups S where
$S= \lambda \mathbb K_0$, where λ is a square. In such a case, all elements of S are squares. What remains to be characterized are those minimal subquasigroups S where ![]() $0\in S$ and all non-zero elements are non-squares.
$0\in S$ and all non-zero elements are non-squares.
The mapping ![]() $x\mapsto x\zeta$ yields an isomorphism
$x\mapsto x\zeta$ yields an isomorphism ![]() $Q_{a,b}\cong Q_{b,a}$ and sends S to
$Q_{a,b}\cong Q_{b,a}$ and sends S to ![]() $S\zeta$. Applying the earlier part of the proof to
$S\zeta$. Applying the earlier part of the proof to ![]() $Q_{b,a}$ yields
$Q_{b,a}$ yields ![]() $S\zeta = \lambda \mathbb K_1$, where λ is a square.
$S\zeta = \lambda \mathbb K_1$, where λ is a square.
Theorem 5.5. Let ![]() $Q =Q_{a,b}$ be a quadratic quasigroup over
$Q =Q_{a,b}$ be a quadratic quasigroup over ![]() $\mathbb F$ that is not a Netto quasigroup. Let
$\mathbb F$ that is not a Netto quasigroup. Let ![]() $\mathbb K$,
$\mathbb K$, ![]() $\mathbb K_0$ and
$\mathbb K_0$ and ![]() $\mathbb K_1$ be the subfields generated by
$\mathbb K_1$ be the subfields generated by ![]() $\{a,b\}$,
$\{a,b\}$, ![]() $\{a\}$ and
$\{a\}$ and ![]() $\{b\}$, respectively. Suppose that there exists a 2-generated subquasigroup of Q that is neither trivial nor minimal. Then all such subquasigroups are exactly the sets
$\{b\}$, respectively. Suppose that there exists a 2-generated subquasigroup of Q that is neither trivial nor minimal. Then all such subquasigroups are exactly the sets ![]() $\lambda \mathbb K + \mu$, where
$\lambda \mathbb K + \mu$, where ![]() $\lambda \in \mathbb F^*$ and
$\lambda \in \mathbb F^*$ and ![]() $\mu \in \mathbb F$. Furthermore, each of
$\mu \in \mathbb F$. Furthermore, each of ![]() $-1$, a, b,
$-1$, a, b, ![]() $1-a$ and
$1-a$ and ![]() $1-b$ is a square in
$1-b$ is a square in ![]() $\mathbb F$. There are two possibilities:
$\mathbb F$. There are two possibilities:
(i)
 $\mathbb K_1$ consists of squares only and
$\mathbb K_1$ consists of squares only and  $\mathbb K_0$ contains a non-square. In this case
$\mathbb K_0$ contains a non-square. In this case  $\mathbb K$ is generated, as a subquasigroup, by
$\mathbb K$ is generated, as a subquasigroup, by  $\{0,s\}$ where
$\{0,s\}$ where  $s\in \mathbb K$, if and only if
$s\in \mathbb K$, if and only if  $\chi(s) = 1$. In particular,
$\chi(s) = 1$. In particular,  $\mathbb K$ is generated by
$\mathbb K$ is generated by  $\{0,1\}$. The minimal subquasigroups of Q are exactly the sets
$\{0,1\}$. The minimal subquasigroups of Q are exactly the sets  $\zeta \mathbb K_1 + \mu$, where
$\zeta \mathbb K_1 + \mu$, where  $\mu,\zeta \in \mathbb F$ and
$\mu,\zeta \in \mathbb F$ and  $\chi(\zeta) = -1$.
$\chi(\zeta) = -1$.(ii)
 $\mathbb K_0$ consists of squares only and
$\mathbb K_0$ consists of squares only and  $\mathbb K_1$ contains a non-square. In this case,
$\mathbb K_1$ contains a non-square. In this case,  $\mathbb K$ is generated, as a subquasigroup, by
$\mathbb K$ is generated, as a subquasigroup, by  $\{0,\zeta\}$, where
$\{0,\zeta\}$, where  $\zeta \in \mathbb K$, if and only if
$\zeta \in \mathbb K$, if and only if  $\chi(\zeta) = -1$. The minimal subquasigroups of Q are exactly the sets
$\chi(\zeta) = -1$. The minimal subquasigroups of Q are exactly the sets  $s\mathbb K_0 + \mu$, where
$s\mathbb K_0 + \mu$, where  $\mu,s \in \mathbb F$ and
$\mu,s \in \mathbb F$ and  $\chi(s) = 1$.
$\chi(s) = 1$.
Proof. Let S be a 2-generated subquasigroup that is not minimal. We shall first investigate the situation when S is generated by 0 and 1. The treatment is divided into a sequence of claims. The case of general S is considered at the end of the proof.
Claim 1.
S is generated by any set ![]() $\{0,s\}$, where
$\{0,s\}$, where ![]() $s\in S$ is a non-zero square.
$s\in S$ is a non-zero square.
Consider the automorphism ![]() $x\mapsto sx$, which sends
$x\mapsto sx$, which sends ![]() $\{0,1\}$ to
$\{0,1\}$ to ![]() $\{0,s\}$. The claim follows from Lemma 5.1.
$\{0,s\}$. The claim follows from Lemma 5.1.
Claim 2.
S contains a non-square.
Assume the contrary. Then there exists a minimal subquasigroup of Q that is contained in S and is generated by ![]() $\{0,c\}$, c a square. That cannot happen, by Claim 1.
$\{0,c\}$, c a square. That cannot happen, by Claim 1.
Claim 3.
(a) ![]() $\chi(x)\geqslant 0$ for all
$\chi(x)\geqslant 0$ for all ![]() $x\in \mathbb K_1$; and
$x\in \mathbb K_1$; and
(b) A set M containing ![]() $0$ is a minimal subquasigroup of Q if and only if there exists
$0$ is a minimal subquasigroup of Q if and only if there exists ![]() $\zeta\in \mathbb F$ such that
$\zeta\in \mathbb F$ such that ![]() $M=\zeta\mathbb K_1\ \text{and }\chi(\zeta) = -1$.
$M=\zeta\mathbb K_1\ \text{and }\chi(\zeta) = -1$.
There must be some minimal subquasigroup M 0 of Q satisfying ![]() $0 \in M_0\subset S$. Every non-zero element of M 0 is a non-square, by Claim 1. Consider a non-zero
$0 \in M_0\subset S$. Every non-zero element of M 0 is a non-square, by Claim 1. Consider a non-zero ![]() $\zeta \in M_0$, and note that
$\zeta \in M_0$, and note that ![]() $\zeta^{-1} M_0$ consists of squares only. The isomorphism
$\zeta^{-1} M_0$ consists of squares only. The isomorphism ![]() $Q_{a,b}\cong
Q_{b,a}$,
$Q_{a,b}\cong
Q_{b,a}$, ![]() $x\mapsto \zeta^{-1} x$, sends M 0 to the minimal subquasigroup of
$x\mapsto \zeta^{-1} x$, sends M 0 to the minimal subquasigroup of ![]() $Q_{b,a}$ generated by 0 and 1. By Lemma 5.3,
$Q_{b,a}$ generated by 0 and 1. By Lemma 5.3, ![]() $\zeta^{-1} M_0 = \mathbb K_1$, and hence
$\zeta^{-1} M_0 = \mathbb K_1$, and hence ![]() $M_0 = \zeta \mathbb K_1$ and Claim 3(a) holds. For any square
$M_0 = \zeta \mathbb K_1$ and Claim 3(a) holds. For any square ![]() $c\in \mathbb F^*$, we know that
$c\in \mathbb F^*$, we know that ![]() $c\zeta\mathbb K_1$ is a minimal subquasigroup of Q, by Proposition 2.1(iii), which proves the ‘if’ part of Claim 3(b).
$c\zeta\mathbb K_1$ is a minimal subquasigroup of Q, by Proposition 2.1(iii), which proves the ‘if’ part of Claim 3(b).
For the converse direction, consider a minimal subquasigroup ![]() $M\ni0$. If M contains a non-square ζ, then
$M\ni0$. If M contains a non-square ζ, then ![]() $M=\zeta \mathbb K_1$, since we already know that
$M=\zeta \mathbb K_1$, since we already know that ![]() $\zeta \mathbb K_1$ is a minimal subquasigroup. If M contains a non-zero square c, then
$\zeta \mathbb K_1$ is a minimal subquasigroup. If M contains a non-zero square c, then ![]() $\{0,1\}\subseteq c^{-1}M$. That would imply that
$\{0,1\}\subseteq c^{-1}M$. That would imply that ![]() $S\subseteq c^{-1}M$, which is impossible because S is not minimal, but
$S\subseteq c^{-1}M$, which is impossible because S is not minimal, but ![]() $c^{-1}M$ is minimal.
$c^{-1}M$ is minimal.
Claim 4.
All of the elements ![]() $-1$, a, b,
$-1$, a, b, ![]() $1-a$ and
$1-a$ and ![]() $1-b$ are squares.
$1-b$ are squares.
Suppose that −1 is a non-square. By Proposition 3.3, then there exists an automorphism of Q that sends 0 to ζ and 1 to 0, for each non-square ![]() $\zeta \in S$. That contradicts Claim 3(b), given that S is not minimal. Thus, −1 is a square. We already know from Claim 3(a) that b is a square. Hence, a is a square too. To see that
$\zeta \in S$. That contradicts Claim 3(b), given that S is not minimal. Thus, −1 is a square. We already know from Claim 3(a) that b is a square. Hence, a is a square too. To see that ![]() $1-a$ and
$1-a$ and ![]() $1-b$ are squares as well, consider the opposite quasigroup, using Proposition 2.1(v).
$1-b$ are squares as well, consider the opposite quasigroup, using Proposition 2.1(v).
Set
 \begin{equation}
\begin{gathered}
N_1=\{x\in S:\chi(x) = -1\},\quad S_1=\{x\in S:\chi(x)=1\},\\
N_0 = N_1\cup\{0\}\quad \text{and}\quad S_0 = S_1\cup\{0\}.
\end{gathered}
\end{equation}
\begin{equation}
\begin{gathered}
N_1=\{x\in S:\chi(x) = -1\},\quad S_1=\{x\in S:\chi(x)=1\},\\
N_0 = N_1\cup\{0\}\quad \text{and}\quad S_0 = S_1\cup\{0\}.
\end{gathered}
\end{equation}Claim 5.
S is the least subquasigroup containing N0.
If ![]() $c\in S_1$, then cS = S, by Lemma 5.1. This implies that
$c\in S_1$, then cS = S, by Lemma 5.1. This implies that ![]() $\zeta S_1 \subseteq S$, for every
$\zeta S_1 \subseteq S$, for every ![]() $\zeta \in N_1$. Since
$\zeta \in N_1$. Since ![]() $\zeta S_1 \subseteq N_1$, we have
$\zeta S_1 \subseteq N_1$, we have ![]() $|S_1| = |\zeta S_1| \leqslant |N_1|$. Therefore,
$|S_1| = |\zeta S_1| \leqslant |N_1|$. Therefore, ![]() $|N_0| \gt |S|/2$, which means that N 0 cannot be contained in a proper subquasigroup of S.
$|N_0| \gt |S|/2$, which means that N 0 cannot be contained in a proper subquasigroup of S.
Claim 6.
If ![]() $c\in \mathbb K_1\setminus\{0\}$, then cS = S. In particular,
$c\in \mathbb K_1\setminus\{0\}$, then cS = S. In particular, ![]() $\mathbb K_1\leqslant S$.
$\mathbb K_1\leqslant S$.
By Claim 5, N 0 generates S. If ![]() $\zeta \in N_1$ and
$\zeta \in N_1$ and ![]() $c\in\mathbb K_1\setminus\{0\}$, then
$c\in\mathbb K_1\setminus\{0\}$, then ![]() $c\zeta$ is in
$c\zeta$ is in ![]() $\zeta\mathbb K_1$, which is minimal by Claim 3(b) and hence generated by 0 and ζ. But
$\zeta\mathbb K_1$, which is minimal by Claim 3(b) and hence generated by 0 and ζ. But ![]() $\{0,\zeta\}\subseteq S$, so
$\{0,\zeta\}\subseteq S$, so ![]() $c\zeta\in S$, and it then follows from Claim 3(a) that
$c\zeta\in S$, and it then follows from Claim 3(a) that ![]() $cN_1=N_1$. Hence, also cS = S, by Lemma 5.1.
$cN_1=N_1$. Hence, also cS = S, by Lemma 5.1.
Claim 7.
If ![]() $s\in S_0$, then
$s\in S_0$, then ![]() $s+S = S$.
$s+S = S$.
Choosing ![]() $c=-1$ yields
$c=-1$ yields ![]() $-S = S$, by Claim 6. The quasigroup S is thus generated by
$-S = S$, by Claim 6. The quasigroup S is thus generated by ![]() $\{0,-s\}$, in view of Claim 1 and Claim 4. Denote by ψ the automorphism
$\{0,-s\}$, in view of Claim 1 and Claim 4. Denote by ψ the automorphism ![]() $x\mapsto x+s$. Since
$x\mapsto x+s$. Since ![]() $\psi(0) = s$ and
$\psi(0) = s$ and ![]() $\psi(-s) = 0$, we have
$\psi(-s) = 0$, we have ![]() $S=\psi(S)
=s+S$, by Lemma 5.1.
$S=\psi(S)
=s+S$, by Lemma 5.1.
Claim 8.
![]() $S=\mathbb K$.
$S=\mathbb K$.
Both a and b are squares that belong to S. Since cS = S whenever ![]() $c\in S$ is a square,
$c\in S$ is a square, ![]() $a^ib^j \in S_0$ for all integers
$a^ib^j \in S_0$ for all integers ![]() $i\geqslant 0$ and
$i\geqslant 0$ and ![]() $j\geqslant 0$. A sum of such elements belongs to S by Claim 7. By Lemma 5.2,
$j\geqslant 0$. A sum of such elements belongs to S by Claim 7. By Lemma 5.2, ![]() $\mathbb K$ is a subquasigroup and
$\mathbb K$ is a subquasigroup and ![]() $\mathbb K\subseteq S$. Since
$\mathbb K\subseteq S$. Since ![]() $\{0,1\}\subseteq\mathbb K$, we must have
$\{0,1\}\subseteq\mathbb K$, we must have ![]() $S \subseteq \mathbb K$.
$S \subseteq \mathbb K$.
Recall that ![]() $\mathbb K_0$ denotes the subfield generated by a. If
$\mathbb K_0$ denotes the subfield generated by a. If ![]() $\mathbb K_0$ consists of squares only, then
$\mathbb K_0$ consists of squares only, then ![]() $\mathbb K_0$ is a subquasigroup of Q. That cannot be, by Claim 2, since
$\mathbb K_0$ is a subquasigroup of Q. That cannot be, by Claim 2, since ![]() $\{0,1\}\subseteq\mathbb K_0$.
$\{0,1\}\subseteq\mathbb K_0$.
Let ![]() $S^{\prime}$ be any subquasigroup of Q with
$S^{\prime}$ be any subquasigroup of Q with ![]() $0\in S^{\prime}$.
$0\in S^{\prime}$.
Claim 9.
The subquasigroup ![]() $S^{\prime}$ is minimal if and only if
$S^{\prime}$ is minimal if and only if ![]() $S^{\prime}=\zeta \mathbb K_1$ for a non-square ζ. Also
$S^{\prime}=\zeta \mathbb K_1$ for a non-square ζ. Also ![]() $S^{\prime}$ is
$S^{\prime}$ is ![]() $2$-generated non-minimal if and only if
$2$-generated non-minimal if and only if ![]() $S^{\prime}=\lambda \mathbb K$, where
$S^{\prime}=\lambda \mathbb K$, where ![]() $\lambda \in \mathbb F^*$.
$\lambda \in \mathbb F^*$.
The first equivalence corresponds to Claim 3(b). Now ![]() $S = \mathbb K$ and S contains some non-square ζ. For any
$S = \mathbb K$ and S contains some non-square ζ. For any ![]() $\lambda\in\mathbb F^*$, one of
$\lambda\in\mathbb F^*$, one of ![]() $\lambda S$ or
$\lambda S$ or ![]() $(\lambda\zeta^{-1})S$ is a subquasigroup isomorphic to S, by Proposition 2.1(iii). However,
$(\lambda\zeta^{-1})S$ is a subquasigroup isomorphic to S, by Proposition 2.1(iii). However, ![]() $(\lambda\zeta^{-1})S=(\lambda\zeta^{-1})\zeta S=\lambda S$ because
$(\lambda\zeta^{-1})S=(\lambda\zeta^{-1})\zeta S=\lambda S$ because ![]() $S=\mathbb K$ is a field. It follows that
$S=\mathbb K$ is a field. It follows that ![]() $\lambda \mathbb K$ is a 2-generated non-minimal subquasigroup of Q for all
$\lambda \mathbb K$ is a 2-generated non-minimal subquasigroup of Q for all ![]() $\lambda\in\mathbb F^*$.
$\lambda\in\mathbb F^*$.
Next suppose that ![]() $S^{\prime}\ni0$ is a non-minimal subquasigroup generated by elements 0 and λ. Let
$S^{\prime}\ni0$ is a non-minimal subquasigroup generated by elements 0 and λ. Let ![]() $S^{\prime\prime}=\lambda^{-1} S^{\prime}$. Note that λ must be a square since otherwise 0 and λ would generate the minimal subquasigroup
$S^{\prime\prime}=\lambda^{-1} S^{\prime}$. Note that λ must be a square since otherwise 0 and λ would generate the minimal subquasigroup ![]() $\lambda\mathbb K_1$, by Claim 3(b). So
$\lambda\mathbb K_1$, by Claim 3(b). So ![]() $x\mapsto\lambda^{-1} x$ is an isomorphism
$x\mapsto\lambda^{-1} x$ is an isomorphism ![]() $S^{\prime}\cong S^{\prime\prime}$, and it maps
$S^{\prime}\cong S^{\prime\prime}$, and it maps ![]() $0,\lambda$ to
$0,\lambda$ to ![]() $0,1$. Hence
$0,1$. Hence ![]() $S^{\prime\prime}=S=\mathbb K$ and
$S^{\prime\prime}=S=\mathbb K$ and ![]() $S^{\prime}=\lambda\mathbb K$.
$S^{\prime}=\lambda\mathbb K$.
It remains to consider the case when ![]() $S^{\prime}\ni0$ is a non-minimal subquasigroup generated by two general elements x and y. By Proposition 2.1(ii), S ʹ is isomorphic to
$S^{\prime}\ni0$ is a non-minimal subquasigroup generated by two general elements x and y. By Proposition 2.1(ii), S ʹ is isomorphic to ![]() $S^{\prime\prime\prime}=S^{\prime}-x$. Now
$S^{\prime\prime\prime}=S^{\prime}-x$. Now ![]() $S^{\prime\prime\prime}$ is a non-minimal subquasigroup generated by 0 and y − x, so by the previous case
$S^{\prime\prime\prime}$ is a non-minimal subquasigroup generated by 0 and y − x, so by the previous case ![]() $S^{\prime\prime\prime}=(y-x)\mathbb K$. But
$S^{\prime\prime\prime}=(y-x)\mathbb K$. But ![]() $0\in S^{\prime}=(y-x)\mathbb K+x$, so
$0\in S^{\prime}=(y-x)\mathbb K+x$, so ![]() $-x(y-x)^{-1}\in\mathbb K$. But
$-x(y-x)^{-1}\in\mathbb K$. But ![]() $\mathbb K$ is closed under addition, so
$\mathbb K$ is closed under addition, so ![]() $S^{\prime}=(y-x)(\mathbb K-x(y-x)^{-1})+x=(y-x)\mathbb K$, which completes the proof of Claim 9.
$S^{\prime}=(y-x)(\mathbb K-x(y-x)^{-1})+x=(y-x)\mathbb K$, which completes the proof of Claim 9.
Let us now turn to the general case. Recall that S is a subquasigroup generated by two distinct elements that is not minimal, but we no longer assume it is generated by ![]() $\{0,1\}$. Clearly, it may be assumed that there exists
$\{0,1\}$. Clearly, it may be assumed that there exists ![]() $\xi \in \mathbb F^*$ such that S is generated by
$\xi \in \mathbb F^*$ such that S is generated by ![]() $\{0,\xi\}$. If ξ is a square, then the subquasigroup
$\{0,\xi\}$. If ξ is a square, then the subquasigroup ![]() $S\xi^{-1}$ generated by 0 and 1 is also not minimal, and that allows us to use the characterization developed above. Hence, we may suppose that ξ is a non-square in
$S\xi^{-1}$ generated by 0 and 1 is also not minimal, and that allows us to use the characterization developed above. Hence, we may suppose that ξ is a non-square in ![]() $\mathbb F$. Then
$\mathbb F$. Then ![]() $S\xi^{-1}$ is a subquasigroup of
$S\xi^{-1}$ is a subquasigroup of ![]() $Q_{b,a}$ that is generated by 0 and 1 and is not minimal. Therefore,
$Q_{b,a}$ that is generated by 0 and 1 and is not minimal. Therefore, ![]() $S\xi^{-1} = \mathbb K$. Since
$S\xi^{-1} = \mathbb K$. Since ![]() $\mathbb K$ contains a non-square, say ζ, we have
$\mathbb K$ contains a non-square, say ζ, we have ![]() $S=\mathbb K\xi = \mathbb K c$, where
$S=\mathbb K\xi = \mathbb K c$, where ![]() $c = \zeta\xi$ is a square. Hence,
$c = \zeta\xi$ is a square. Hence, ![]() $\mathbb K$ is a subquasigroup of Q that is 2-generated but not minimal.
$\mathbb K$ is a subquasigroup of Q that is 2-generated but not minimal.
In ![]() $Q_{b,a}$, the proper minimal subquasigroups of
$Q_{b,a}$, the proper minimal subquasigroups of ![]() $\mathbb K$ containing 0 are exactly all of the sets
$\mathbb K$ containing 0 are exactly all of the sets ![]() $\mathbb K_0\xi$, where ξ is a non-square. Furthermore, the field
$\mathbb K_0\xi$, where ξ is a non-square. Furthermore, the field ![]() $\mathbb K_0$ consists of squares only. The minimal subquasigroups of Q that include 0 are thus equal to
$\mathbb K_0$ consists of squares only. The minimal subquasigroups of Q that include 0 are thus equal to ![]() $s\mathbb K_0$, where
$s\mathbb K_0$, where ![]() $\chi(s) = 1$.
$\chi(s) = 1$.
Theorems 5.4 and 5.5 describe the structure of minimal subquasigroups in all quadratic quasigroups that are not Netto quasigroups. The subfield ![]() $\mathbb K$ generated by a and b has a clear structural meaning in all these quasigroups except those that are described by Theorem 5.4(ii) and fulfil
$\mathbb K$ generated by a and b has a clear structural meaning in all these quasigroups except those that are described by Theorem 5.4(ii) and fulfil ![]() $\mathbb K_0\ne \mathbb K_1$. Note that
$\mathbb K_0\ne \mathbb K_1$. Note that ![]() $\mathbb K_0=\mathbb K_1$ for all affine quasigroups
$\mathbb K_0=\mathbb K_1$ for all affine quasigroups ![]() $Q_{a,a}$, and hence Theorem 5.5 implies that all 2-generated subquasigroups of
$Q_{a,a}$, and hence Theorem 5.5 implies that all 2-generated subquasigroups of ![]() $Q_{a,a}$ are minimal.
$Q_{a,a}$ are minimal.
Affine lines and semilinear mappings
Suppose that ![]() $Q=Q_{a,b}$ is a quadratic quasigroup that contains minimal subquasigroups of two different orders. Theorems 5.4 and 5.5 implies that
$Q=Q_{a,b}$ is a quadratic quasigroup that contains minimal subquasigroups of two different orders. Theorems 5.4 and 5.5 implies that ![]() $\mathbb K_0\ne \mathbb K_1$, where
$\mathbb K_0\ne \mathbb K_1$, where ![]() $\mathbb K_0$ is the least subfield containing a, and
$\mathbb K_0$ is the least subfield containing a, and ![]() $\mathbb K_1$ the least subfield containing b and that both these subfields consist of squares only. The existence of a subfield consisting only of squares implies that
$\mathbb K_1$ the least subfield containing b and that both these subfields consist of squares only. The existence of a subfield consisting only of squares implies that ![]() $|\mathbb F| = q^2$ and that
$|\mathbb F| = q^2$ and that ![]() $\mathbb K_0 \cup \mathbb K_1\subseteq\mathbb F_q$.
$\mathbb K_0 \cup \mathbb K_1\subseteq\mathbb F_q$.
For distinct ![]() $x,y\in \mathbb F$ denote by
$x,y\in \mathbb F$ denote by ![]() $S(x,y)$ the subquasigroup S generated by x and y. Put
$S(x,y)$ the subquasigroup S generated by x and y. Put ![]() $\lambda = y -x$. As follows from Theorem 5.4,
$\lambda = y -x$. As follows from Theorem 5.4, ![]() $S = \lambda\mathbb K_0 + x$ if
$S = \lambda\mathbb K_0 + x$ if ![]() $\chi(\lambda) = 1$ and
$\chi(\lambda) = 1$ and ![]() $S = \lambda\mathbb K_1 + x$ if
$S = \lambda\mathbb K_1 + x$ if ![]() $\chi(\lambda) = -1$.
$\chi(\lambda) = -1$.
Call a set ![]() $B\subseteq \mathbb F$ saturated if there exists
$B\subseteq \mathbb F$ saturated if there exists ![]() $i \in \{0,1\}$ such that for any distinct
$i \in \{0,1\}$ such that for any distinct ![]() $x,y \in B$, both
$x,y \in B$, both ![]() $|S(x,y)|=|\mathbb K_i|$ and
$|S(x,y)|=|\mathbb K_i|$ and ![]() $S(x,y)\subseteq B$ are true.
$S(x,y)\subseteq B$ are true.
It follows from the above description of subquasigroups ![]() $S(x,y)$ that any set
$S(x,y)$ that any set ![]() $\lambda \mathbb F_q + \mu$ is saturated, provided
$\lambda \mathbb F_q + \mu$ is saturated, provided ![]() $\lambda \in \mathbb F^*$ and
$\lambda \in \mathbb F^*$ and ![]() $\mu \in \mathbb F$. This may be converted:
$\mu \in \mathbb F$. This may be converted:
Lemma 5.6. A q-element set ![]() $B\subseteq \mathbb F$ is saturated if and only if there exist
$B\subseteq \mathbb F$ is saturated if and only if there exist ![]() $\lambda \in \mathbb F^*$ and
$\lambda \in \mathbb F^*$ and ![]() $\mu \in \mathbb F$ such that
$\mu \in \mathbb F$ such that ![]() $B = \lambda \mathbb F_q
+ \mu$.
$B = \lambda \mathbb F_q
+ \mu$.
Proof. Let B be saturated. By the definition of a saturated set, there exists ![]() $\varepsilon \in \{-1,1\}$ such that
$\varepsilon \in \{-1,1\}$ such that ![]() $\chi(y-x) = \varepsilon$ whenever
$\chi(y-x) = \varepsilon$ whenever ![]() $x,y \in B$ and
$x,y \in B$ and ![]() $x\ne y$. Every q-element set with the latter property is equal to a set of the form
$x\ne y$. Every q-element set with the latter property is equal to a set of the form ![]() $\lambda \mathbb F_q+ \mu$, where
$\lambda \mathbb F_q+ \mu$, where ![]() $\lambda \ne 0$, by a theorem of Blokhuis [Reference Blokhuis3].
$\lambda \ne 0$, by a theorem of Blokhuis [Reference Blokhuis3].
Corollary 5.7. Let ![]() $Q_{a,b}$ be a quasigroup over
$Q_{a,b}$ be a quasigroup over ![]() $\mathbb F$ such that
$\mathbb F$ such that ![]() $Q_{a,b}$ contains minimal subquasigroups of two different orders. Then there exists q > 1 such that
$Q_{a,b}$ contains minimal subquasigroups of two different orders. Then there exists q > 1 such that ![]() $|\mathbb F| = q^2$, and
$|\mathbb F| = q^2$, and ![]() $\operatorname{Aut}(Q)$ acts on the set of all affine lines
$\operatorname{Aut}(Q)$ acts on the set of all affine lines ![]() $\lambda \mathbb F_q + \mu$, where
$\lambda \mathbb F_q + \mu$, where ![]() $\lambda \in \mathbb F^*$ and
$\lambda \in \mathbb F^*$ and ![]() $\mu \in \mathbb F$.
$\mu \in \mathbb F$.
Proof. This follows from Lemma 5.6 since each automorphism of Q maps a saturated set to a saturated set.
Let K be a subfield of ![]() $\mathbb F$. A permutation σ of
$\mathbb F$. A permutation σ of ![]() $\mathbb F$ is said to be K-semilinear if σ is additive and there exists
$\mathbb F$ is said to be K-semilinear if σ is additive and there exists ![]() $\alpha \in \operatorname{Aut}(K)$ such that
$\alpha \in \operatorname{Aut}(K)$ such that ![]() $\sigma(\lambda x) =
\alpha(\lambda)\sigma(x)$ for all
$\sigma(\lambda x) =
\alpha(\lambda)\sigma(x)$ for all ![]() $x\in \mathbb F$ and
$x\in \mathbb F$ and ![]() $\lambda \in K$.
$\lambda \in K$.
Note that if ![]() $L \subseteq K \subseteq \mathbb F$ are fields, and σ is a K-semilinear permutation of
$L \subseteq K \subseteq \mathbb F$ are fields, and σ is a K-semilinear permutation of ![]() $\mathbb F$, then σ is L-semilinear too.
$\mathbb F$, then σ is L-semilinear too.
Proposition 5.8. Let ![]() $\psi\in \operatorname{Aut}(Q)$, where
$\psi\in \operatorname{Aut}(Q)$, where ![]() $Q= Q_{a,b}$ is a quadratic quasigroup defined on
$Q= Q_{a,b}$ is a quadratic quasigroup defined on ![]() $\mathbb F$ that is not a Netto quasigroup. Let
$\mathbb F$ that is not a Netto quasigroup. Let ![]() $\mathbb K$ be the subfield of
$\mathbb K$ be the subfield of ![]() $\mathbb F$ generated by a and b. Then there exists
$\mathbb F$ generated by a and b. Then there exists ![]() $\mu \in \mathbb F$ and a
$\mu \in \mathbb F$ and a ![]() $\mathbb K$-semilinear mapping σ such that
$\mathbb K$-semilinear mapping σ such that ![]() $\psi(x) = \sigma(x) + \mu$ for all
$\psi(x) = \sigma(x) + \mu$ for all ![]() $x\in \mathbb F$.
$x\in \mathbb F$.
Proof. If ![]() $Q=Q_{a,b}$ is 2-generated, use Theorem 4.7. Suppose that Q is not 2-generated. If all minimal subquasigroups of Q are of the same order, put
$Q=Q_{a,b}$ is 2-generated, use Theorem 4.7. Suppose that Q is not 2-generated. If all minimal subquasigroups of Q are of the same order, put ![]() $K = \mathbb K$. If there is no common order, denote by K the subfield of
$K = \mathbb K$. If there is no common order, denote by K the subfield of ![]() $\mathbb F$ that is of order q, where
$\mathbb F$ that is of order q, where ![]() $|\mathbb F| = q^2$. Then ψ maps an affine line of K to an affine line of K. This is true for quasigroups in which all 2-generated subquasigroups are minimal by Theorem 5.4 and Theorem 5.7 since ψ preserves the structure of minimal subquasigroups. The other cases follow from Theorem 5.5 since ψ also preserves the structure of 2-generated subquasigroups that are not minimal. By The Fundamental Theorem of Affine Geometry [Reference Artin2], there thus exist
$|\mathbb F| = q^2$. Then ψ maps an affine line of K to an affine line of K. This is true for quasigroups in which all 2-generated subquasigroups are minimal by Theorem 5.4 and Theorem 5.7 since ψ preserves the structure of minimal subquasigroups. The other cases follow from Theorem 5.5 since ψ also preserves the structure of 2-generated subquasigroups that are not minimal. By The Fundamental Theorem of Affine Geometry [Reference Artin2], there thus exist ![]() $\mu\in \mathbb F$ and a K-semilinear permutation σ of
$\mu\in \mathbb F$ and a K-semilinear permutation σ of ![]() $\mathbb F$ such that
$\mathbb F$ such that ![]() $\psi(x) = \sigma(x)+\mu$ for all
$\psi(x) = \sigma(x)+\mu$ for all ![]() $x\in \mathbb F$.
$x\in \mathbb F$.
6. Automorphisms and isomorphisms
This section proves Theorems 1.2 and 1.1. The proof of Theorem 1.2 is done separately for the affine case, twisted case, and all other situations. As shown in Lemma 2.7, Steiner quadratic quasigroups that are not affine are induced by Netto systems and fulfil the condition of Theorem 1.1. As mentioned in Section 1, the automorphism group of a Netto system is known [Reference Robinson11] and conforms with our statement of Theorem 1.2. Netto quasigroups are thus not discussed in this section.
The proof of Theorem 1.2 has two parts: first we have to verify that certain mappings are automorphisms, and second we have to show that there are no other automorphisms. In view of Proposition 2.1, to achieve the first goal, only the affine and twisted cases need to be considered. For the affine case ![]() $x*y = x+a(y-x)$, so it is clear that any
$x*y = x+a(y-x)$, so it is clear that any ![]() $\mathbb K$-linear map σ is an automorphism,
$\mathbb K$-linear map σ is an automorphism, ![]() $\mathbb K$ being the least subfield containing a. The second part of the proof of Theorem 1.2 for affine quasigroups follows directly from Proposition 6.2(ii) below.
$\mathbb K$ being the least subfield containing a. The second part of the proof of Theorem 1.2 for affine quasigroups follows directly from Proposition 6.2(ii) below.
Recall that ![]() $Q = Q_{a,b}$ is called twisted if
$Q = Q_{a,b}$ is called twisted if ![]() $\mathbb K$, the subfield generated by a, is of order γ 2 and
$\mathbb K$, the subfield generated by a, is of order γ 2 and ![]() $b = a^\gamma$. The meaning of γ is considered to be fixed throughout this section, whenever Q is twisted.
$b = a^\gamma$. The meaning of γ is considered to be fixed throughout this section, whenever Q is twisted.
To see that every permutation described in Theorem 1.2 is an automorphism of ![]() $Q_{a,b}$ it thus remains to verify the existence of automorphisms that generalize the automorphisms induced by the structure of a quadratic nearfield:
$Q_{a,b}$ it thus remains to verify the existence of automorphisms that generalize the automorphisms induced by the structure of a quadratic nearfield:
Lemma 6.1. Let ![]() $Q = Q_{a,b}$ be a twisted quadratic quasigroup over
$Q = Q_{a,b}$ be a twisted quadratic quasigroup over ![]() $\mathbb F$. Then
$\mathbb F$. Then ![]() $x\mapsto \zeta x^\gamma + \mu$ is an automorphism of Q whenever ζ is a non-square in
$x\mapsto \zeta x^\gamma + \mu$ is an automorphism of Q whenever ζ is a non-square in ![]() $\mathbb F$ and
$\mathbb F$ and ![]() $\mu \in
\mathbb F$.
$\mu \in
\mathbb F$.
Proof. It may be assumed that µ = 0. Let ![]() $x,y\in \mathbb F$ be distinct elements. Put i = 0 if
$x,y\in \mathbb F$ be distinct elements. Put i = 0 if ![]() $\chi(y-x)=1$, and i = 1 if
$\chi(y-x)=1$, and i = 1 if ![]() $\chi(y-x)=-1$. Then
$\chi(y-x)=-1$. Then  $x*y = x + a^{\gamma^i}(y-x)$ and
$x*y = x + a^{\gamma^i}(y-x)$ and
 \begin{equation*} \zeta(x*y)^\gamma = \zeta x^\gamma + \zeta b^{\gamma^i}(y-x)^\gamma =
\zeta x^\gamma + b^{\gamma^i}(\zeta y^\gamma -\zeta x^\gamma)=
\zeta x^\gamma * \zeta y^\gamma,\end{equation*}
\begin{equation*} \zeta(x*y)^\gamma = \zeta x^\gamma + \zeta b^{\gamma^i}(y-x)^\gamma =
\zeta x^\gamma + b^{\gamma^i}(\zeta y^\gamma -\zeta x^\gamma)=
\zeta x^\gamma * \zeta y^\gamma,\end{equation*} since ![]() $\chi(y^\gamma-x^\gamma)=\chi((y-x)^\gamma)=\chi(y-x)$ because γ is odd.
$\chi(y^\gamma-x^\gamma)=\chi((y-x)^\gamma)=\chi(y-x)$ because γ is odd.
Proposition 6.2. Let ![]() $Q=Q_{a,b}$ be a quadratic quasigroup over
$Q=Q_{a,b}$ be a quadratic quasigroup over ![]() $\mathbb F$ that is not a Netto quasigroup. Denote by
$\mathbb F$ that is not a Netto quasigroup. Denote by ![]() $\mathbb K$ the subfield of
$\mathbb K$ the subfield of ![]() $\mathbb F$ that is generated by a and b. Let
$\mathbb F$ that is generated by a and b. Let ![]() $\psi\in \operatorname{Aut}(Q)$ be such that
$\psi\in \operatorname{Aut}(Q)$ be such that ![]() $\psi(0)=0$. Then:
$\psi(0)=0$. Then:
(i)
 $\psi(1)$ is a square in
$\psi(1)$ is a square in  $\mathbb F$ if Q is neither affine nor twisted; and
$\mathbb F$ if Q is neither affine nor twisted; and(ii) ψ is
 $\mathbb K$-linear if a = b or if
$\mathbb K$-linear if a = b or if  $\psi(1)$ is a square in
$\psi(1)$ is a square in  $\mathbb F$.
$\mathbb F$.
Proof. Point (i) coincides with Proposition 4.5. Put ![]() $\lambda = \psi(1)$. Point (ii) will be first proved under the assumption that all minimal subquasigroups of Q are of the same order. In this case,
$\lambda = \psi(1)$. Point (ii) will be first proved under the assumption that all minimal subquasigroups of Q are of the same order. In this case, ![]() $\psi(\mathbb K) = \lambda \mathbb K$ by Theorems 5.4 and 5.5 since a minimal subquasigroup is mapped to a minimal subquasigroup and a 2-generated subquasigroup is mapped to a 2-generated subquasigroup. The mapping
$\psi(\mathbb K) = \lambda \mathbb K$ by Theorems 5.4 and 5.5 since a minimal subquasigroup is mapped to a minimal subquasigroup and a 2-generated subquasigroup is mapped to a 2-generated subquasigroup. The mapping ![]() $x\mapsto \lambda^{-1} \psi(x)$ hence is an automorphism of Q that sends the 2-generated subquasigroup
$x\mapsto \lambda^{-1} \psi(x)$ hence is an automorphism of Q that sends the 2-generated subquasigroup ![]() $\mathbb K$ to itself. The restriction of the latter mapping to
$\mathbb K$ to itself. The restriction of the latter mapping to ![]() $\mathbb K$ is
$\mathbb K$ is ![]() $\mathbb K$-linear by Theorem 4.7. Since the mapping is
$\mathbb K$-linear by Theorem 4.7. Since the mapping is ![]() $\mathbb K$-semilinear, by Proposition 5.8, it has to be a
$\mathbb K$-semilinear, by Proposition 5.8, it has to be a ![]() $\mathbb K$-linear automorphism of Q. Hence, ψ is
$\mathbb K$-linear automorphism of Q. Hence, ψ is ![]() $\mathbb K$-linear as well.
$\mathbb K$-linear as well.
Let us now assume that Q contains minimal subquasigroups of two distinct sizes. Let ![]() $\alpha\in \operatorname{Aut}(\mathbb K)$ be the automorphism such that
$\alpha\in \operatorname{Aut}(\mathbb K)$ be the automorphism such that ![]() $\psi(cx) = \alpha(c)\psi(x)$ for all
$\psi(cx) = \alpha(c)\psi(x)$ for all ![]() $c\in \mathbb K$. In this case,
$c\in \mathbb K$. In this case, ![]() $|\mathbb F|=q^2$ for some q > 2 and
$|\mathbb F|=q^2$ for some q > 2 and ![]() $\psi(\mathbb F_q) = \lambda\mathbb F_q$ by Corollary 5.7. Hence,
$\psi(\mathbb F_q) = \lambda\mathbb F_q$ by Corollary 5.7. Hence, ![]() $x\mapsto \lambda^{-1} \psi(x)$ is a
$x\mapsto \lambda^{-1} \psi(x)$ is a ![]() $\mathbb K$-semilinear mapping with automorphism α, the restriction of which yields an automorphism of
$\mathbb K$-semilinear mapping with automorphism α, the restriction of which yields an automorphism of ![]() $(\mathbb F_q,*)$ such that
$(\mathbb F_q,*)$ such that ![]() $x*y = x+a(y-x)$ for all
$x*y = x+a(y-x)$ for all ![]() $x,y \in \mathbb F_q$. Therefore,
$x,y \in \mathbb F_q$. Therefore, ![]() $\alpha(a) = a$, by the earlier part of this proof. To finish it suffices to show that
$\alpha(a) = a$, by the earlier part of this proof. To finish it suffices to show that ![]() $\alpha(b) = b$ too. To that end, choose a non-square
$\alpha(b) = b$ too. To that end, choose a non-square ![]() $\zeta \in \mathbb F$ and note that
$\zeta \in \mathbb F$ and note that ![]() $\psi(\zeta \mathbb F_q) = \lambda^{\prime} \zeta \mathbb F_q$ for a square
$\psi(\zeta \mathbb F_q) = \lambda^{\prime} \zeta \mathbb F_q$ for a square ![]() $\lambda^{\prime}$, by Corollary 5.7. The mapping
$\lambda^{\prime}$, by Corollary 5.7. The mapping ![]() $x\mapsto \zeta^{-1} (\lambda^{\prime})^{-1} \psi(\zeta x)$ is an automorphism of
$x\mapsto \zeta^{-1} (\lambda^{\prime})^{-1} \psi(\zeta x)$ is an automorphism of ![]() $Q_{b,a}$ that sends
$Q_{b,a}$ that sends ![]() $\mathbb F_q$ to
$\mathbb F_q$ to ![]() $\mathbb F_q$ and is associated, as a
$\mathbb F_q$ and is associated, as a ![]() $\mathbb K$-semilinear mapping, with the automorphism
$\mathbb K$-semilinear mapping, with the automorphism ![]() $\alpha \in \operatorname{Aut}(\mathbb K)$. Since b is now in the position of a, we must have
$\alpha \in \operatorname{Aut}(\mathbb K)$. Since b is now in the position of a, we must have ![]() $\alpha(b) = b$.
$\alpha(b) = b$.
For non-affine cases, the following fact is of crucial importance.
Lemma 6.3. Suppose that ![]() $\sigma\colon\mathbb F\to \mathbb F$ is bijective and additive. If
$\sigma\colon\mathbb F\to \mathbb F$ is bijective and additive. If
then there exist ![]() $\alpha \in \operatorname{Aut}(\mathbb F)$ and
$\alpha \in \operatorname{Aut}(\mathbb F)$ and ![]() $\lambda
\in \mathbb F$ such that
$\lambda
\in \mathbb F$ such that ![]() $\sigma(x) = \lambda\alpha(x)$ for each
$\sigma(x) = \lambda\alpha(x)$ for each ![]() $x\in \mathbb F^*$ and
$x\in \mathbb F^*$ and ![]() $\chi(\lambda) = 1$.
$\chi(\lambda) = 1$.
Proof. The set of all additive permutations σ of ![]() $\mathbb F$ that satisfy Condition (6.1) forms a group. This group contains the mapping
$\mathbb F$ that satisfy Condition (6.1) forms a group. This group contains the mapping ![]() $x\mapsto\lambda x$ for each
$x\mapsto\lambda x$ for each ![]() $\lambda \in \mathbb F^*$, with
$\lambda \in \mathbb F^*$, with ![]() $\chi(\lambda) = 1$. Since
$\chi(\lambda) = 1$. Since ![]() $\chi(\sigma(1))=\chi(\sigma(1)-\sigma(0))=\chi(1)=1$, it suffices to prove the statement under the assumption that
$\chi(\sigma(1))=\chi(\sigma(1)-\sigma(0))=\chi(1)=1$, it suffices to prove the statement under the assumption that ![]() $\sigma(1) = 1$. However, if σ is a permutation of
$\sigma(1) = 1$. However, if σ is a permutation of ![]() $\mathbb F$ such that
$\mathbb F$ such that ![]() $\sigma(0) = 0$,
$\sigma(0) = 0$, ![]() $\sigma(1) = 1$ and Condition (6.1) holds, then
$\sigma(1) = 1$ and Condition (6.1) holds, then ![]() $\sigma\in \operatorname{Aut}(\mathbb F)$ as shown by Carlitz [Reference Carlitz4].
$\sigma\in \operatorname{Aut}(\mathbb F)$ as shown by Carlitz [Reference Carlitz4].
Lemma 6.4. Let ![]() $Q=Q_{a,b}$ be a non-affine quadratic quasigroup over
$Q=Q_{a,b}$ be a non-affine quadratic quasigroup over ![]() $\mathbb F$ that is not a Steiner quasigroup. Denote by
$\mathbb F$ that is not a Steiner quasigroup. Denote by ![]() $\mathbb K$ the least subfield of
$\mathbb K$ the least subfield of ![]() $\mathbb F$ containing a and b. If
$\mathbb F$ containing a and b. If ![]() $\sigma \in \operatorname{Aut}(Q)$ is
$\sigma \in \operatorname{Aut}(Q)$ is ![]() $\mathbb K$-linear, then σ satisfies Equation (6.1).
$\mathbb K$-linear, then σ satisfies Equation (6.1).
Proof. If ![]() $\chi(v-u) = 1$, then
$\chi(v-u) = 1$, then ![]() $\sigma(u*v)=\sigma(u+a(v-u)) = \sigma(u)+a(\sigma(v)-\sigma(u))$. Hence,
$\sigma(u*v)=\sigma(u+a(v-u)) = \sigma(u)+a(\sigma(v)-\sigma(u))$. Hence, ![]() $\sigma(u*v) = \sigma(u)*\sigma(v)$ implies that
$\sigma(u*v) = \sigma(u)*\sigma(v)$ implies that ![]() $\chi(\sigma(v)-\sigma(u)) = 1$. The argument when
$\chi(\sigma(v)-\sigma(u)) = 1$. The argument when ![]() $\chi(v-u) = -1$ is similar.
$\chi(v-u) = -1$ is similar.
Lemma 6.5. Let ![]() $Q = Q_{a,b}$ be a non-affine quadratic quasigroup over
$Q = Q_{a,b}$ be a non-affine quadratic quasigroup over ![]() $\mathbb F$ that is neither Steiner nor twisted. Let
$\mathbb F$ that is neither Steiner nor twisted. Let ![]() $\mathbb K$ be the subfield generated by a and b. Then
$\mathbb K$ be the subfield generated by a and b. Then ![]() $\operatorname{Aut}(Q) =\mathrm A \Gamma^2 \mathrm L_1(\mathbb F\,{\mid}\, \mathbb K)$.
$\operatorname{Aut}(Q) =\mathrm A \Gamma^2 \mathrm L_1(\mathbb F\,{\mid}\, \mathbb K)$.
Proof. Let ![]() $\psi \in \operatorname{Aut}(Q)$ be such that
$\psi \in \operatorname{Aut}(Q)$ be such that ![]() $\psi(0) = 0$. Then ψ is
$\psi(0) = 0$. Then ψ is ![]() $\mathbb K$-linear by Proposition 6.2 and is a square scalar multiple of some
$\mathbb K$-linear by Proposition 6.2 and is a square scalar multiple of some ![]() $\alpha \in \operatorname{Aut}(\mathbb F)$ by Lemmas 6.4 and 6.3.
$\alpha \in \operatorname{Aut}(\mathbb F)$ by Lemmas 6.4 and 6.3.
Lemma 6.6. Let ![]() $Q = Q_{a,b}$ be a twisted quasigroup over
$Q = Q_{a,b}$ be a twisted quasigroup over ![]() $\mathbb F$. Then
$\mathbb F$. Then ![]() $\operatorname{Aut}(Q) = \mathrm A \Gamma \mathrm L^{\mathrm{tw}}_1(\mathbb F\,{\mid}\, \mathbb K)$.
$\operatorname{Aut}(Q) = \mathrm A \Gamma \mathrm L^{\mathrm{tw}}_1(\mathbb F\,{\mid}\, \mathbb K)$.
Proof. Let ![]() $\psi \in \operatorname{Aut}(Q)$ be such that
$\psi \in \operatorname{Aut}(Q)$ be such that ![]() $\psi(0) = 0$. If
$\psi(0) = 0$. If ![]() $\psi(1)$ is a square, then
$\psi(1)$ is a square, then ![]() $\psi\in \mathrm A \Gamma^2 \mathrm L_1(\mathbb F\,{\mid}\, \mathbb K)$, by the same argument as in the proof of Lemma 6.5. Suppose that
$\psi\in \mathrm A \Gamma^2 \mathrm L_1(\mathbb F\,{\mid}\, \mathbb K)$, by the same argument as in the proof of Lemma 6.5. Suppose that ![]() $\zeta = \psi(1)$ is a non-square and compose ψ with the mapping
$\zeta = \psi(1)$ is a non-square and compose ψ with the mapping ![]() $\sigma\colon x\mapsto (\zeta^{-1})^\gamma x^\gamma$. Then
$\sigma\colon x\mapsto (\zeta^{-1})^\gamma x^\gamma$. Then ![]() $\sigma \psi \in
\operatorname{Aut}(Q)$ by Lemma 6.1 and
$\sigma \psi \in
\operatorname{Aut}(Q)$ by Lemma 6.1 and ![]() $\sigma\in \mathrm A \Gamma \mathrm L^{\mathrm{tw}}_1(\mathbb F\,{\mid}\, \mathbb K)$. Since
$\sigma\in \mathrm A \Gamma \mathrm L^{\mathrm{tw}}_1(\mathbb F\,{\mid}\, \mathbb K)$. Since ![]() $\sigma\psi(1) = 1$ is a square,
$\sigma\psi(1) = 1$ is a square, ![]() $\sigma\psi \in \mathrm A \Gamma^2 \mathrm L_1(\mathbb F\,{\mid}\, \mathbb K)$. These facts imply that ψ belongs to
$\sigma\psi \in \mathrm A \Gamma^2 \mathrm L_1(\mathbb F\,{\mid}\, \mathbb K)$. These facts imply that ψ belongs to ![]() $\mathrm A \Gamma \mathrm L^{\mathrm{tw}}_1(\mathbb F\,{\mid}\, \mathbb K)$.
$\mathrm A \Gamma \mathrm L^{\mathrm{tw}}_1(\mathbb F\,{\mid}\, \mathbb K)$.
This finishes the proof of Theorem 1.2. What follows is a proof of Theorem 1.1.
Proof. As mentioned at the beginning of this section, it may be assumed that a = b if ![]() $Q = Q_{a,b}$ is a Steiner quasigroup. The subfield generated by a and b is denoted by
$Q = Q_{a,b}$ is a Steiner quasigroup. The subfield generated by a and b is denoted by ![]() $\mathbb K$.
$\mathbb K$.
Let ![]() $\zeta \in \mathbb F$ be a non-square. Since
$\zeta \in \mathbb F$ be a non-square. Since ![]() $x\mapsto \zeta x$ maps isomorphically
$x\mapsto \zeta x$ maps isomorphically ![]() $Q_{a,b}$ to
$Q_{a,b}$ to ![]() $Q_{b,a}$ and
$Q_{b,a}$ and ![]() $Q_{c,d}$ to
$Q_{c,d}$ to ![]() $Q_{d,c}$, certain assumptions may be made. By Theorem 5.5, it may be assumed that if Q possesses a 2-generated subquasigroup that is not minimal, then
$Q_{d,c}$, certain assumptions may be made. By Theorem 5.5, it may be assumed that if Q possesses a 2-generated subquasigroup that is not minimal, then ![]() $\mathbb K$ carries one such subquasigroup. It may also be assumed that there exists an isomorphism
$\mathbb K$ carries one such subquasigroup. It may also be assumed that there exists an isomorphism ![]() $\sigma\colon Q_{a,b}\cong Q_{c,d}$ that sends 0 to 0 and 1 to a square in
$\sigma\colon Q_{a,b}\cong Q_{c,d}$ that sends 0 to 0 and 1 to a square in ![]() $\mathbb F$. Since scalar multiplication by a non-zero square is an automorphism of
$\mathbb F$. Since scalar multiplication by a non-zero square is an automorphism of ![]() $Q_{c,d}$, it may be assumed, in fact, that
$Q_{c,d}$, it may be assumed, in fact, that ![]() $\sigma(0) = 0$ and
$\sigma(0) = 0$ and ![]() $\sigma(1) = 1$.
$\sigma(1) = 1$.
Suppose that Q does not contain minimal subquasigroups of distinct orders. Then ![]() $\mathbb K$ coincides with the subquasigroup generated by 0 and 1, by Theorems 5.4 and 5.5. By these theorems,
$\mathbb K$ coincides with the subquasigroup generated by 0 and 1, by Theorems 5.4 and 5.5. By these theorems, ![]() $\sigma(\mathbb K) = \mathbb K$ since
$\sigma(\mathbb K) = \mathbb K$ since ![]() $\sigma(\mathbb K)$ is a subquasigroup of
$\sigma(\mathbb K)$ is a subquasigroup of ![]() $Q_{c,d}$ that is generated by 0 and 1. Applying Theorem 4.8 to the restriction of σ to
$Q_{c,d}$ that is generated by 0 and 1. Applying Theorem 4.8 to the restriction of σ to ![]() $\mathbb K$ yields
$\mathbb K$ yields ![]() $\alpha\in \operatorname{Aut}(\mathbb K)$ such that
$\alpha\in \operatorname{Aut}(\mathbb K)$ such that ![]() $c = \alpha(a)$ and
$c = \alpha(a)$ and ![]() $d = \alpha(b)$. This suffices, since α may be extended to an automorphism of
$d = \alpha(b)$. This suffices, since α may be extended to an automorphism of ![]() $\mathbb F$.
$\mathbb F$.
Suppose now that Q contains minimal subquasigroups of two different orders. Then ![]() $|\mathbb F| = q^2$ for some q > 2, and in Q, there exists a unique saturated set of order q that contains both 0 and 1. This set is equal to
$|\mathbb F| = q^2$ for some q > 2, and in Q, there exists a unique saturated set of order q that contains both 0 and 1. This set is equal to ![]() $\mathbb F_q$. Since σ maps a saturated set to a saturated set, it must be that
$\mathbb F_q$. Since σ maps a saturated set to a saturated set, it must be that ![]() $\sigma(\mathbb F_q) = \mathbb F_q$. The orders of minimal subquasigroups contained in
$\sigma(\mathbb F_q) = \mathbb F_q$. The orders of minimal subquasigroups contained in ![]() $\mathbb F_q$ are thus the same in both
$\mathbb F_q$ are thus the same in both ![]() $Q_{a,b}$ and
$Q_{a,b}$ and ![]() $Q_{c,d}$. By interpreting an affine line
$Q_{c,d}$. By interpreting an affine line ![]() $\lambda \mathbb F_q +\mu$ as a saturated set, we therefore obtain that for all
$\lambda \mathbb F_q +\mu$ as a saturated set, we therefore obtain that for all ![]() $\lambda \in \mathbb F^*$ and
$\lambda \in \mathbb F^*$ and ![]() $\mu \in \mathbb F$ there exist
$\mu \in \mathbb F$ there exist ![]() $\lambda^{\prime} \in \mathbb F^*$ and
$\lambda^{\prime} \in \mathbb F^*$ and ![]() $\mu^{\prime}\in \mathbb F$ such that
$\mu^{\prime}\in \mathbb F$ such that ![]() $\chi(\lambda) = \chi(\lambda^{\prime})$ and
$\chi(\lambda) = \chi(\lambda^{\prime})$ and ![]() $\sigma(\lambda \mathbb F_q+\mu)
= \lambda^{\prime}\mathbb F_q + \mu^{\prime}$. This means that σ fulfils condition (6.1). Since
$\sigma(\lambda \mathbb F_q+\mu)
= \lambda^{\prime}\mathbb F_q + \mu^{\prime}$. This means that σ fulfils condition (6.1). Since ![]() $\sigma(0) = 0$ and
$\sigma(0) = 0$ and ![]() $\sigma(1) =1$, the theorem of Carlitz [Reference Carlitz4] implies that
$\sigma(1) =1$, the theorem of Carlitz [Reference Carlitz4] implies that ![]() $\sigma \in \operatorname{Aut}(\mathbb F)$. To get
$\sigma \in \operatorname{Aut}(\mathbb F)$. To get ![]() $\sigma(a) = c$ consider the quasigroup product of 0 and 1. To obtain
$\sigma(a) = c$ consider the quasigroup product of 0 and 1. To obtain ![]() $\sigma(b) = d$, multiply 0 and ζ.
$\sigma(b) = d$, multiply 0 and ζ.
7. Concluding comments
The theory developed in this paper should prove to be useful in the many applications of quadratic quasigroups [Reference Allsop and Wanless1, Reference Drápal and Wanless5, Reference Evans7–Reference Gill and Wanless9, Reference Wanless14]. In [Reference Wanless14], methods were developed for distinguishing isomorphism classes of quasigroups generated from cyclotomic orthomorphisms. In the quadratic case, this is now a very simple task, given Theorem 1.1. It would be of interest to develop similar methods for quasigroups generated from other cyclotomic orthomorphisms. Another feature of [Reference Wanless14] is that commutative, semisymmetric and totally symmetric quasigroups played a prominent role, as they did in the current work. It thus should prove useful to have the characterizations in Theorem 1.3.
It was mentioned in the introduction that this paper grew out of a need in [Reference Drápal and Wanless5] to understand when quadratic quasigroups are isomorphic to each other. In that paper, we showed that, asymptotically, a non-zero constant fraction of the choices for the pair (a, b), result in ![]() $Q_{a,b}$ having a special property called maximal non-associativity. We conjectured that removing isomorphs would not reduce the demonstrated number of examples by more than a factor proportional to
$Q_{a,b}$ having a special property called maximal non-associativity. We conjectured that removing isomorphs would not reduce the demonstrated number of examples by more than a factor proportional to ![]() $\log|\mathbb F|$. Thanks to Theorem 1.1, we now know this conjecture to be true, since the automorphism group of
$\log|\mathbb F|$. Thanks to Theorem 1.1, we now know this conjecture to be true, since the automorphism group of ![]() $\mathbb F$ has order
$\mathbb F$ has order ![]() $O(\log|\mathbb F|)$.
$O(\log|\mathbb F|)$.
Funding Statement
A. Drápal supported by INTER-EXCELLENCE project LTAUSA19070 MŠMT Czech Republic.