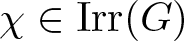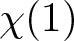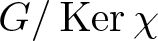1. Introduction
A classical theorem of Broline and Garrison implies that if an irreducible character χ of a finite group G has maximal degree then ![]() $\operatorname{Ker}\chi$ is nilpotent (Corollary 12.20 of [Reference Isaacs1]). This result was extended by Isaacs, who considered characters of nth maximal degree in [Reference Isaacs2], and proved that if
$\operatorname{Ker}\chi$ is nilpotent (Corollary 12.20 of [Reference Isaacs1]). This result was extended by Isaacs, who considered characters of nth maximal degree in [Reference Isaacs2], and proved that if ![]() $\chi\in{{\operatorname{Irr}}}(G)$ has nth maximal degree, then the Fitting height of the solvable radical of
$\chi\in{{\operatorname{Irr}}}(G)$ has nth maximal degree, then the Fitting height of the solvable radical of ![]() $\operatorname{Ker}\chi$ is at most n.
$\operatorname{Ker}\chi$ is at most n.
Our goal in this note is to consider irreducible characters at the other extreme. Of course, if ![]() $\chi\in{{\operatorname{Irr}}}(G)$ is linear, then
$\chi\in{{\operatorname{Irr}}}(G)$ is linear, then ![]() $G'\leq\operatorname{Ker}\chi$ and
$G'\leq\operatorname{Ker}\chi$ and ![]() $G/\operatorname{Ker}\chi$ is abelian. But can we restrict the structure of
$G/\operatorname{Ker}\chi$ is abelian. But can we restrict the structure of ![]() $G/\operatorname{Ker}\chi$ if
$G/\operatorname{Ker}\chi$ if ![]() $\chi(1)$ is “small”? This is the content of our main result. We write
$\chi(1)$ is “small”? This is the content of our main result. We write ![]() $m(G)=\min\{\chi(1)\mid\chi\in{{\operatorname{Irr}}}(G), \chi(1) \gt 1\}$. We say that
$m(G)=\min\{\chi(1)\mid\chi\in{{\operatorname{Irr}}}(G), \chi(1) \gt 1\}$. We say that ![]() $\chi\in{{\operatorname{Irr}}}(G)$ is a minimal character if
$\chi\in{{\operatorname{Irr}}}(G)$ is a minimal character if ![]() $\chi(1)=m(G)$.
$\chi(1)=m(G)$.
Theorem A. Let G be a solvable finite group. Suppose that m(G) is odd. If ![]() $\chi\in{{\operatorname{Irr}}}(G)$ is a minimal character, then
$\chi\in{{\operatorname{Irr}}}(G)$ is a minimal character, then ![]() $G/\operatorname{Ker}\chi$ is nilpotent-by-abelian.
$G/\operatorname{Ker}\chi$ is nilpotent-by-abelian.
As ![]() $\operatorname{GL}_2(3)$ shows, some hypothesis on m(G) is definitely necessary. The Frobenius group of order 20 acting faithfully on an extraspecial 2-group of order 25 is an example with faithful minimal characters of degree 4. We do not know whether it is enough to assume that m(G) is not a power of 2. On the other hand, some solvability hypothesis is definitely necessary: consider any non-abelian simple group with odd degree minimal characters (for instance,
$\operatorname{GL}_2(3)$ shows, some hypothesis on m(G) is definitely necessary. The Frobenius group of order 20 acting faithfully on an extraspecial 2-group of order 25 is an example with faithful minimal characters of degree 4. We do not know whether it is enough to assume that m(G) is not a power of 2. On the other hand, some solvability hypothesis is definitely necessary: consider any non-abelian simple group with odd degree minimal characters (for instance, ![]() $\mathsf{A}_5$). Theorem A follows from applying the next result to
$\mathsf{A}_5$). Theorem A follows from applying the next result to ![]() $G/\operatorname{Ker}\chi$.
$G/\operatorname{Ker}\chi$.
Theorem B. Let G be a finite solvable group. Suppose that ![]() $\chi\in{{\operatorname{Irr}}}(G)$ is a faithful minimal character. If
$\chi\in{{\operatorname{Irr}}}(G)$ is a faithful minimal character. If ![]() $\chi(1)$ is odd, then G is nilpotent-by-abelian.
$\chi(1)$ is odd, then G is nilpotent-by-abelian.
Note that the structure of groups with all minimal characters faithful was described in detail by Robinson in [Reference Robinson6, Reference Robinson7]. In particular, as shown in Lemma 2.1 of [Reference Robinson6], solvable groups with all minimal characters faithful are nilpotent-by-abelian. The examples mentioned above show that this is not the case if we just assume that G has a minimal faithful character. Our proof of Theorem B relies on some of the ideas developed by Robinson.
2. Proofs
We argue as in Lemma 2 of [Reference Robinson7] to prove our first lemma.
Lemma 2.1. Let G be a finite group. Suppose that ![]() $\chi\in{{\operatorname{Irr}}}(G)$ is a primitive faithful minimal character of G. If
$\chi\in{{\operatorname{Irr}}}(G)$ is a primitive faithful minimal character of G. If ![]() $N\trianglelefteq G$ is non-central, then
$N\trianglelefteq G$ is non-central, then ![]() $\chi_N\in{{\operatorname{Irr}}}(N)$.
$\chi_N\in{{\operatorname{Irr}}}(N)$.
Proof. Suppose that ![]() $\chi_N\not\in{{\operatorname{Irr}}}(N)$. Then there exists a central extension
$\chi_N\not\in{{\operatorname{Irr}}}(N)$. Then there exists a central extension ![]() $G^*$ of G and
$G^*$ of G and ![]() $\alpha,\beta\in{{\operatorname{Irr}}}(G^*)$ such that
$\alpha,\beta\in{{\operatorname{Irr}}}(G^*)$ such that ![]() $\chi=\alpha\beta$, where
$\chi=\alpha\beta$, where ![]() $\alpha,\beta$ are primitive nonlinear irreducible characters of
$\alpha,\beta$ are primitive nonlinear irreducible characters of ![]() $G^*$. Without loss of generality, we may assume that
$G^*$. Without loss of generality, we may assume that ![]() $\alpha(1)\leq\chi(1)^{1/2}$. Since
$\alpha(1)\leq\chi(1)^{1/2}$. Since ![]() $1_{G^*}$ is an irreducible constituent of
$1_{G^*}$ is an irreducible constituent of ![]() $\alpha\overline{\alpha}$, the minimality of
$\alpha\overline{\alpha}$, the minimality of ![]() $\chi(1)$ implies that
$\chi(1)$ implies that ![]() $\alpha\overline{\alpha}$ is a sum of linear characters. Hence
$\alpha\overline{\alpha}$ is a sum of linear characters. Hence ![]() $(G^*)'\leq\operatorname{Ker}(\alpha\overline{\alpha})$. In particular,
$(G^*)'\leq\operatorname{Ker}(\alpha\overline{\alpha})$. In particular, ![]() $(G^*)'\leq{\mathbf{Z}}(\alpha)$. By Lemma 2.27 of [Reference Isaacs1],
$(G^*)'\leq{\mathbf{Z}}(\alpha)$. By Lemma 2.27 of [Reference Isaacs1], ![]() ${\mathbf{Z}}(\alpha)/\operatorname{Ker}\alpha\leq{\mathbf{Z}}(G^*/\operatorname{Ker}\alpha)$. If follows that
${\mathbf{Z}}(\alpha)/\operatorname{Ker}\alpha\leq{\mathbf{Z}}(G^*/\operatorname{Ker}\alpha)$. If follows that ![]() $G^*/\operatorname{Ker}\alpha$ is nilpotent (of class at most 2). But α is nonlinear and primitive. This contradicts Theorem 6.22 of [Reference Isaacs1].
$G^*/\operatorname{Ker}\alpha$ is nilpotent (of class at most 2). But α is nonlinear and primitive. This contradicts Theorem 6.22 of [Reference Isaacs1].
Next, we handle the primitive case of Theorem B. We refer the reader to [Reference Isaacs3] for the definition and basic properties of Gajendragadkar’s p-special characters.
Lemma 2.2. Let G be a solvable group. Suppose that ![]() $\chi\in{{\operatorname{Irr}}}(G)$ is a primitive faithful minimal character. Then
$\chi\in{{\operatorname{Irr}}}(G)$ is a primitive faithful minimal character. Then ![]() $\chi(1)$ is a power of a prime p. Furthermore, if p > 2, then G is nilpotent-by-abelian.
$\chi(1)$ is a power of a prime p. Furthermore, if p > 2, then G is nilpotent-by-abelian.
Proof. We may assume that ![]() $\chi(1) \gt 1$. By Theorem 2.17 of [Reference Isaacs3], χ factors as a product of p-special characters, where p runs over the set of prime divisors of
$\chi(1) \gt 1$. By Theorem 2.17 of [Reference Isaacs3], χ factors as a product of p-special characters, where p runs over the set of prime divisors of ![]() $\chi(1)$. Since
$\chi(1)$. Since ![]() $\chi(1)=m(G)$, it follows that
$\chi(1)=m(G)$, it follows that ![]() $\chi(1)=p^n$ is a power of a prime p. This proves the first part of the lemma.
$\chi(1)=p^n$ is a power of a prime p. This proves the first part of the lemma.
Suppose now that p > 2. Let q ≠ p be a prime. Then ![]() $\chi_{\mathbf{O}_q(G)}$ is not irreducible. It follows from Lemma 2.1 that
$\chi_{\mathbf{O}_q(G)}$ is not irreducible. It follows from Lemma 2.1 that ![]() $\mathbf{O}_q(G)$ is central in G. Hence
$\mathbf{O}_q(G)$ is central in G. Hence ![]() ${\mathbf{F}}(G)=E{\mathbf{Z}}(G)$, where
${\mathbf{F}}(G)=E{\mathbf{Z}}(G)$, where ![]() $E=\mathbf{O}_p(G)$. Furthermore, using again Lemma 2.1, every normal abelian subgroup of G is central. Since G has a faithful irreducible character, Theorem 2.32 of [Reference Isaacs1] implies that
$E=\mathbf{O}_p(G)$. Furthermore, using again Lemma 2.1, every normal abelian subgroup of G is central. Since G has a faithful irreducible character, Theorem 2.32 of [Reference Isaacs1] implies that ![]() ${\mathbf{Z}}(G)$ is cyclic. Now, Corollary 1.10 of [Reference Manz and Wolf5] implies that E is extraspecial of exponent p. Since
${\mathbf{Z}}(G)$ is cyclic. Now, Corollary 1.10 of [Reference Manz and Wolf5] implies that E is extraspecial of exponent p. Since ![]() $\chi_E\in{{\operatorname{Irr}}}(E)$, we necessarily have that
$\chi_E\in{{\operatorname{Irr}}}(E)$, we necessarily have that ![]() $|E|=p^{2n+1}$.
$|E|=p^{2n+1}$.
Note that ![]() ${\mathbf{C}}_G(E)={\mathbf{C}}_G({\mathbf{F}}(G))={\mathbf{Z}}(G)$, so
${\mathbf{C}}_G(E)={\mathbf{C}}_G({\mathbf{F}}(G))={\mathbf{Z}}(G)$, so ![]() $G/{\mathbf{Z}}(G)$ is isomorphic to a subgroup of
$G/{\mathbf{Z}}(G)$ is isomorphic to a subgroup of ![]() ${{\operatorname{Aut}}}_{{\mathbf{Z}}(E)}(E)$. By [Reference Winter8], using again that p > 2, we deduce that
${{\operatorname{Aut}}}_{{\mathbf{Z}}(E)}(E)$. By [Reference Winter8], using again that p > 2, we deduce that ![]() $G/{\mathbf{F}}(G)$ is isomorphic to a subgroup of
$G/{\mathbf{F}}(G)$ is isomorphic to a subgroup of ![]() $\operatorname{Sp}(2n,p)$. By [Reference Landazuri and Seitz4],
$\operatorname{Sp}(2n,p)$. By [Reference Landazuri and Seitz4], ![]() $\operatorname{Sp}(2n,p)$ has a faithful irreducible representation of dimension
$\operatorname{Sp}(2n,p)$ has a faithful irreducible representation of dimension ![]() $(p^n-1)/2$. Hence
$(p^n-1)/2$. Hence ![]() $G/{\mathbf{F}}(G)$ has a faithful character of degree
$G/{\mathbf{F}}(G)$ has a faithful character of degree ![]() $\leq (p^n-1)/2$. Since
$\leq (p^n-1)/2$. Since ![]() $m(G)=p^n$, we conclude that
$m(G)=p^n$, we conclude that ![]() $G/{\mathbf{F}}(G)$ has a faithful character that is a sum of linear characters. We conclude that
$G/{\mathbf{F}}(G)$ has a faithful character that is a sum of linear characters. We conclude that ![]() $G/{\mathbf{F}}(G)$ is abelian, as we wanted to prove.
$G/{\mathbf{F}}(G)$ is abelian, as we wanted to prove.
Now, we complete the proof of a slightly strengthened version of Theorem B.
Theorem 2.3. Let G be a solvable group. Suppose that ![]() $\chi\in{{\operatorname{Irr}}}(G)$ is a faithful minimal character. If χ is induced from an odd degree character, then G is nilpotent-by-abelian.
$\chi\in{{\operatorname{Irr}}}(G)$ is a faithful minimal character. If χ is induced from an odd degree character, then G is nilpotent-by-abelian.
Proof. Let ![]() $H\leq G$ and
$H\leq G$ and ![]() $\beta\in{{\operatorname{Irr}}}(H)$ primitive such that
$\beta\in{{\operatorname{Irr}}}(H)$ primitive such that ![]() $\beta^G=\chi$. Suppose first that
$\beta^G=\chi$. Suppose first that ![]() $\beta(1)=1$, so that
$\beta(1)=1$, so that ![]() $\chi(1)=|G:H|$. Since 1G is an irreducible constituent of
$\chi(1)=|G:H|$. Since 1G is an irreducible constituent of ![]() $(1_H)^G$ and
$(1_H)^G$ and ![]() $m(G)=|G:H|=(1_H)^G(1)$, we deduce that
$m(G)=|G:H|=(1_H)^G(1)$, we deduce that ![]() $(1_H)^G$ is a sum of linear characters. Hence
$(1_H)^G$ is a sum of linear characters. Hence ![]() $G'\leq\operatorname{Ker}(1_H)^G\leq H$. Thus
$G'\leq\operatorname{Ker}(1_H)^G\leq H$. Thus ![]() $H\trianglelefteq G$ and by Clifford’s theorem (Theorem 6.2 of [Reference Isaacs1]), χH is a sum of conjugates of β. In particular, χH is a sum of linear characters, so
$H\trianglelefteq G$ and by Clifford’s theorem (Theorem 6.2 of [Reference Isaacs1]), χH is a sum of conjugates of β. In particular, χH is a sum of linear characters, so ![]() $H'\leq\operatorname{Ker}\chi=1$. Hence G is metabelian and the result follows.
$H'\leq\operatorname{Ker}\chi=1$. Hence G is metabelian and the result follows.
Now, we may assume that ![]() $\beta(1) \gt 1$ is odd. First, we will see that
$\beta(1) \gt 1$ is odd. First, we will see that ![]() $H\trianglelefteq G$ and
$H\trianglelefteq G$ and ![]() $G'=H'$. Note that
$G'=H'$. Note that ![]() $\chi(1)=|G:H|\beta(1) \gt |G:H|$. Hence
$\chi(1)=|G:H|\beta(1) \gt |G:H|$. Hence ![]() $(1_H)^G$ is a sum of linear characters and
$(1_H)^G$ is a sum of linear characters and ![]() $G'\leq H$, as before. In particular,
$G'\leq H$, as before. In particular, ![]() $H\trianglelefteq G$. Thus H ʹ is also normal in G and all the irreducible characters of
$H\trianglelefteq G$. Thus H ʹ is also normal in G and all the irreducible characters of ![]() $G/H'$ have degree divisible by
$G/H'$ have degree divisible by ![]() $|G:H| \lt \chi(1)=m(G)$. Hence,
$|G:H| \lt \chi(1)=m(G)$. Hence, ![]() ${{\operatorname{Irr}}}(G/H')$ is a set of linear characters, and we conclude that
${{\operatorname{Irr}}}(G/H')$ is a set of linear characters, and we conclude that ![]() $G'=H'$, as desired.
$G'=H'$, as desired.
Now, we claim that ![]() $\beta(1)=m(H)$. Let
$\beta(1)=m(H)$. Let ![]() $\mu\in{{\operatorname{Irr}}}(H)$ be nonlinear. Hence, there exists
$\mu\in{{\operatorname{Irr}}}(H)$ be nonlinear. Hence, there exists ![]() $\nu\in{{\operatorname{Irr}}}(G)$ nonlinear such that
$\nu\in{{\operatorname{Irr}}}(G)$ nonlinear such that ![]() $[\mu^G,\nu]\neq 0$. Thus
$[\mu^G,\nu]\neq 0$. Thus
We conclude that ![]() $\beta(1)\leq\mu(1)$. The claim follows.
$\beta(1)\leq\mu(1)$. The claim follows.
Thus β is a primitive faithful minimal character of ![]() $H/\operatorname{Ker}\beta$. By Lemma 2.2, we have that
$H/\operatorname{Ker}\beta$. By Lemma 2.2, we have that ![]() $\beta(1)$ is a power of a prime p. Let
$\beta(1)$ is a power of a prime p. Let ![]() $\beta=\beta_1,\dots,\beta_t$ be the G-conjugates of β. Let
$\beta=\beta_1,\dots,\beta_t$ be the G-conjugates of β. Let ![]() $K_i=\operatorname{Ker}\beta_i$. Since
$K_i=\operatorname{Ker}\beta_i$. Since ![]() $\chi=\beta^G$ is faithful, Lemma 5.11 of [Reference Isaacs1] implies that
$\chi=\beta^G$ is faithful, Lemma 5.11 of [Reference Isaacs1] implies that  $\bigcap_{i=1}^tK_i=1$. Since p > 2, by the second part of Lemma 2.2, we have that
$\bigcap_{i=1}^tK_i=1$. Since p > 2, by the second part of Lemma 2.2, we have that ![]() $H/K_i$ is nilpotent-by-abelian. Write
$H/K_i$ is nilpotent-by-abelian. Write ![]() $F_i/K_i={\mathbf{F}}(H/K_i)$, so that
$F_i/K_i={\mathbf{F}}(H/K_i)$, so that ![]() $G'=H'\leq F_i$ for every i. By Proposition 9.5 of [Reference Manz and Wolf5],
$G'=H'\leq F_i$ for every i. By Proposition 9.5 of [Reference Manz and Wolf5],  $\bigcap_{i=1}^tF_i={\mathbf{F}}(H)$. Therefore,
$\bigcap_{i=1}^tF_i={\mathbf{F}}(H)$. Therefore, ![]() $G'\leq {\mathbf{F}}(H)$ and we conclude that G is nilpotent-by-abelian, as wanted.
$G'\leq {\mathbf{F}}(H)$ and we conclude that G is nilpotent-by-abelian, as wanted.
Funding Statement
Research supported by Ministerio de Ciencia e Innovación (Grant PID2019-103854GB-I00 funded by MCIN/AEI/10.13039/501100011033).