Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Towers, David
1985.
On ideally finite Lie algebras which are lower semi-modular.
Proceedings of the Edinburgh Mathematical Society,
Vol. 28,
Issue. 1,
p.
9.
Kissin, E. V.
1986.
On normed Lie algebras with sufficiently many subalgebras of codimension I.
Proceedings of the Edinburgh Mathematical Society,
Vol. 29,
Issue. 2,
p.
199.
Varea, V. R.
1999.
Lower semimodular Lie algebras.
Proceedings of the Edinburgh Mathematical Society,
Vol. 42,
Issue. 3,
p.
521.
Kissin, Edward
Shulman, Victor S.
and
Turovskii, Yurii V.
2009.
Banach Lie algebras with Lie subalgebras of finite codimension: Their invariant subspaces and Lie ideals.
Journal of Functional Analysis,
Vol. 256,
Issue. 2,
p.
323.
Towers, David A.
2011.
The index complex of a maximal subalgebra of a Lie algebra.
Proceedings of the Edinburgh Mathematical Society,
Vol. 54,
Issue. 2,
p.
531.
Wang, DengYin
Ge, Hui
and
Li, XiaoWei
2012.
Maximal subalgebras of the general linear Lie algebra containing Cartan subalgebras.
Science China Mathematics,
Vol. 55,
Issue. 7,
p.
1381.
Towers, David A.
2012.
Maximal subalgebras of Lie algebras containing Engel subalgebras.
Journal of Pure and Applied Algebra,
Vol. 216,
Issue. 3,
p.
688.
Towers, David A.
2013.
Supplements to Maximal Subalgebras of Lie Algebras.
Communications in Algebra,
Vol. 41,
Issue. 10,
p.
3848.
Goudarzi, Leila
and
Salemkar, Ali Reza
2015.
The Ideal Index of Subalgebras of a Finite Dimensional Lie Algebra.
Communications in Algebra,
Vol. 43,
Issue. 6,
p.
2258.
Chehrazi, Sara
and
Salemkar, Ali Reza
2016.
SCAP-subalgebras of Lie algebras.
Czechoslovak Mathematical Journal,
Vol. 66,
Issue. 4,
p.
1177.
Biyogmam, G. R.
and
Tcheka, C.
2020.
Leibniz algebras with absolute maximal Lie subalgebras.
Algebra and Discrete Mathematics,
Vol. 29,
Issue. 1,
p.
52.


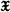 denote the class of finite-dimensional Lie algebras
denote the class of finite-dimensional Lie algebras 