Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-14T06:00:04.130Z Has data issue: false hasContentIssue false
  • English
  • Français

Limits of pure states

Published online by Cambridge University Press:  20 January 2009

R. J. Archbold
R. J. Archbold
Affiliation:
Department of Mathematics, The Edward Wright Building, Dunbar Street, Aberdeen AB9 2TY
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In [7, Section 5], Glimm showed that if φ and ψ are inequivalent pure states of a liminal C*-algebra A such that the Gelfand-Naimark-Segal (GNS) representations πφ and πψ cannot be separated by disjoint open subsets of the spectrum  then ½ (φ+ψ) is a weak*-limit of pure states. We extend this to arbitrary C*-algebras (and more general convex combinations) by means of what we hope will be regarded as a transparent proof based on the notion of transition probabilities. As an application, we show that if J is a proper primal ideal of a separable C*-algebra A then there exists a state φ in 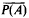(the pure state space) such that J=ker πφ (Theorem 3). The significance of this is discussed below after the introduction of further notation and terminology.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 32 , Issue 2 , June 1989 , pp. 249 - 254
Copyright
Copyright © Edinburgh Mathematical Society 1989

References

REFERENCES

1.Archbold, R. J., Topologies for primal ideals, J. London Math. Soc. (2) 36 (1987), 524–542.CrossRefGoogle Scholar
2.Archbold, R. J. and Batty, C. J. K., On factorial states of operator algebras, III, J. Operator Theory 15 (1986), 53–81.Google Scholar
3.Archbold, R. J. and Batty, C. J. K., Homogeneous states of C*-algebras, Quart. J. Math. Oxford (2) 38 (1987), 259–275.Google Scholar
4.Archbold, R. J. and Shultz, F. W., Characterization of C*-algebras with continuous trace by properties of their pure states, Pacific J. Math., to appear.Google Scholar
5.Batty, C. J. K. and Archbold, R. J., On factorial states of operator algebras, II, J. Operator Theory 13 (1985), 131–142.Google Scholar
6.Dixmier, J., Les C*-algebres et leurs representations, 2nd edition (Gauthier-Villars, Paris, 1969).Google Scholar
7.Glimm, J., Type I C*-algebras, Ann. of Math. 73 (1961), 572–612.Google Scholar
8.Glimm, J. and Kadison, R. V., Unitary operators in C*-algebras, Pacific J. Math. 10 (1960), 547–556.Google Scholar
9.Kadison, R. V., Limits of states, Comm. Math. Phys. 85 (1982), 143–154.Google Scholar
10.Pedersen, G. K., C*-algebras and their automorphism groups (Academic Press, London, 1979).Google Scholar
11.Powers, R. T. and Størmer, E., Free states of the canonical anticommutation relations, Comm. Math. Phys. 16 (1970), 1–33.Google Scholar
12.Shultz, F. W., Pure states as a dual object for C*-algebras, Comm. Math. Phys. 82 (1982), 497–509.Google Scholar