No CrossRef data available.
Published online by Cambridge University Press: 20 January 2009
The basic reciprocity of j-differential and LM-integral

for bounded functions f(x) with simple discontinuities but continuous on the left at each point and for g(x) in the somewhat restricted class B of functions of bounded variation and also left-continuous, was established in (2) and (3); the dot here indicates the lower product of 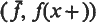 and (jg, g+ (x+)dx), with
and (jg, g+ (x+)dx), with 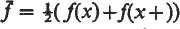 , and the integral indicated is the RJDS-integral, equivalent to (LM)
, and the integral indicated is the RJDS-integral, equivalent to (LM) 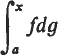 .
.