No CrossRef data available.
Article contents
Local uniqueness in boundary problems†
Published online by Cambridge University Press: 20 January 2009
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
The study of periodic, irrotational waves of finite amplitude in an incompressible fluid of infinite depth was reduced by Levi-Civita (1) to the determination of a function
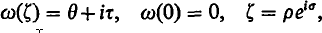
regular analytic in the interior of the unit circle ρ = 1 and which satisfies the condition
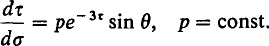
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1970
References
REFERENCES
(1) Levi-Civita, T., Détermination rigoureuse des ondes permanentes d’ampleur finie, Math. Ann. 93 (1925), 264–314.CrossRefGoogle Scholar
(4) Dunninger, D. and Martin, M. H., On a uniqueness question of Levi-Civita, Atti Accad. Naz. Lincei Rend. CI. Sci. Fis. Mat. Natur. (8) 41 (1966), 452–459.Google Scholar
(5) Cushing, J., Local uniqueness for harmonic functions under nonlinear boundary conditions, University of Maryland doctoral thesis (1968).Google Scholar
(6) Martin, M. H. and Trytten, G. N., Inequalities associated with quadratic forms, Atti. Acc. Sc. Torino, Cl. Sci. Fis. Mat. Natur. 101 (1966–1967), 285–290.Google Scholar
(7) Dunninger, D., Uniqueness and comparison theorems for harmonic functions under boundary conditions, J. Math, and Phys. 46 (1967), 299–310.CrossRefGoogle Scholar

