Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Binding, Paul
and
Browne, Patrick J
1989.
Classification of eigentuples for uniformly elliptic multiparameter problems.
Journal of Mathematical Analysis and Applications,
Vol. 139,
Issue. 1,
p.
268.
Binding, Paul
and
Browne, Patrick J.
1989.
Two parameter eigenvalue problems for matrices.
Linear Algebra and its Applications,
Vol. 113,
Issue. ,
p.
139.
Binding, P. A.
Browne, P. J.
Huang, Y. X.
and
Picard, R. H.
1991.
On eigencurves of elliptic boundary value problems.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 118,
Issue. 1-2,
p.
161.
Košir, Tomaž
1994.
Finite-dimensional multiparameter spectral theory: The nonderogatory case.
Linear Algebra and its Applications,
Vol. 212-213,
Issue. ,
p.
45.
Grunenfelder, Luzius
and
Košir, Tomaž
1996.
Recent Developments in Operator Theory and Its Applications.
p.
177.
Binding, Paul
and
Kosir, Tomaz
1996.
Second Root Vectors for Multiparameter Eigenvalue Problems of Fredholm Type.
Transactions of the American Mathematical Society,
Vol. 348,
Issue. 1,
p.
229.
Grunenfelder, Luzius
and
Kosir, Tomaz
1996.
An algebraic approach to multiparameter spectral theory.
Transactions of the American Mathematical Society,
Vol. 348,
Issue. 8,
p.
2983.
2010.
Multiparameter Eigenvalue Problems.
p.
210.
Gungah, Satin K.
Alsubaie, Fawwaz F.
and
Jaimoukha, Imad M.
2024.
On the Two-Parameter Matrix Pencil Problem.
SIAM Journal on Matrix Analysis and Applications,
Vol. 45,
Issue. 3,
p.
1287.

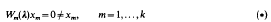
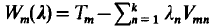 operate in Hilbert spaces
operate in Hilbert spaces 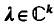 . Previous work on this “uniformly elliptic” class has demonstrated completeness of the decomposable tensors
. Previous work on this “uniformly elliptic” class has demonstrated completeness of the decomposable tensors 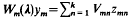 are constructed for the “root subspaces” corresponding to λ∈ℝ
are constructed for the “root subspaces” corresponding to λ∈ℝ