Article contents
Multiplicity and stability of normalized solutions to non-autonomous Schrödinger equation with mixed non-linearities
Published online by Cambridge University Press: 09 November 2023
Abstract
This paper first studies the multiplicity of normalized solutions to the non-autonomous Schrödinger equation with mixed nonlinearities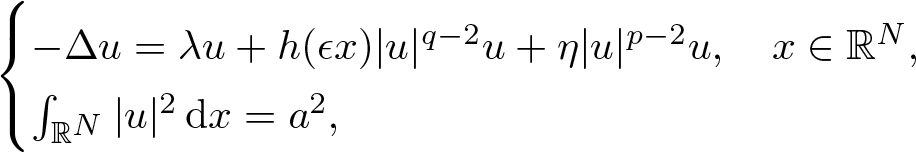 \begin{equation*}\begin{cases}-\Delta u=\lambda u+h(\epsilon x)|u|^{q-2}u+\eta |u|^{p-2}u,\quad x\in \mathbb{R}^N, \\\int_{\mathbb{R}^N}|u|^2\,\textrm{d}x=a^2,\end{cases}\end{equation*}
\begin{equation*}\begin{cases}-\Delta u=\lambda u+h(\epsilon x)|u|^{q-2}u+\eta |u|^{p-2}u,\quad x\in \mathbb{R}^N, \\\int_{\mathbb{R}^N}|u|^2\,\textrm{d}x=a^2,\end{cases}\end{equation*}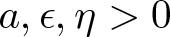 $a, \epsilon, \eta \gt 0$, q is L2-subcritical, p is L2-supercritical,
$a, \epsilon, \eta \gt 0$, q is L2-subcritical, p is L2-supercritical, 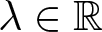 $\lambda\in \mathbb{R}$ is an unknown parameter that appears as a Lagrange multiplier and h is a positive and continuous function. It is proved that the numbers of normalized solutions are at least the numbers of global maximum points of h when ϵ is small enough. The solutions obtained are local minimizers and probably not ground state solutions for the lack of symmetry of the potential h. Secondly, the stability of several different sets consisting of the local minimizers is analysed. Compared with the results of the corresponding autonomous equation, the appearance of the potential h increases the number of the local minimizers and the number of the stable sets. In particular, our results cover the Sobolev critical case
$\lambda\in \mathbb{R}$ is an unknown parameter that appears as a Lagrange multiplier and h is a positive and continuous function. It is proved that the numbers of normalized solutions are at least the numbers of global maximum points of h when ϵ is small enough. The solutions obtained are local minimizers and probably not ground state solutions for the lack of symmetry of the potential h. Secondly, the stability of several different sets consisting of the local minimizers is analysed. Compared with the results of the corresponding autonomous equation, the appearance of the potential h increases the number of the local minimizers and the number of the stable sets. In particular, our results cover the Sobolev critical case 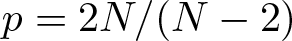 $p=2N/(N-2)$.
$p=2N/(N-2)$.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 67 , Issue 1 , February 2024 , pp. 1 - 27
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society
References
- 8
- Cited by


