No CrossRef data available.
Article contents
Normal  -Fitting classes
-Fitting classes
Published online by Cambridge University Press: 20 January 2009
Abstract
The authors together with M. J. Karbe [Ill. J. Math. 33 (1989) 333–359] have considered Fitting classes 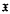 of
of  -groups and, under some rather strong restrictions, obtained an existence and conjugacy theorem for
-groups and, under some rather strong restrictions, obtained an existence and conjugacy theorem for 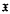 -injectors. Results of Menegazzo and Newell show that these restrictions are, in fact, necessary.
-injectors. Results of Menegazzo and Newell show that these restrictions are, in fact, necessary.
The Fitting class 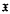 is normal if, for each
is normal if, for each 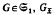 is the unique
is the unique 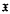 -injector of G.
-injector of G. 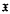 is abelian normal if, for each
is abelian normal if, for each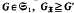 . For finite soluble groups these two concepts coincide but the class of Černikov-by-nilpotent
. For finite soluble groups these two concepts coincide but the class of Černikov-by-nilpotent  -groups is an example of a nonabelian normal Fitting class of
-groups is an example of a nonabelian normal Fitting class of  -groups. In all known examples in which
-groups. In all known examples in which 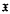 -injectors exist
-injectors exist 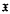 is closely associated with some normal Fitting class (the Černikov-by-nilpotent groups arise from studying the locally nilpotent injectors).
is closely associated with some normal Fitting class (the Černikov-by-nilpotent groups arise from studying the locally nilpotent injectors).
Here we investigate normal Fitting classes further, paying particular attention to the distinctions between abelian and nonabelian normal Fitting classes. Products and intersections with (abelian) normal Fitting classes lead to further examples of Fitting classes satisfying the conditions of the existence and conjugacy theorem.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1992

