Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Dette, Holger
and
Lo Huang, Mong-Na
2000.
Convex Optimal Designs for Compound Polynomial Extrapolation.
Annals of the Institute of Statistical Mathematics,
Vol. 52,
Issue. 3,
p.
557.
Wang, Jun
Meng, Xiaohong
and
Li, Fang
2017.
Fast Nonlinear Generalized Inversion of Gravity Data with Application to the Three-Dimensional Crustal Density Structure of Sichuan Basin, Southwest China.
Pure and Applied Geophysics,
Vol. 174,
Issue. 11,
p.
4101.
Zhou, Chi-Chun
and
Dai, Wu-Sheng
2018.
A statistical mechanical approach to restricted integer partition functions.
Journal of Statistical Mechanics: Theory and Experiment,
Vol. 2018,
Issue. 5,
p.
053111.
Yang, Yishi
Zhu, Hengliang
Bi, Zhaori
Yan, Changhao
Zhou, Dian
Su, Yangfeng
and
Zeng, Xuan
2018.
Smart-MSP: A Self-Adaptive Multiple Starting Point Optimization Approach for Analog Circuit Synthesis.
IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems,
Vol. 37,
Issue. 3,
p.
531.
2021.
New Numerical Scheme with Newton Polynomial.
p.
435.
Atangana, Abdon
and
Araz, Seda İğret
2021.
New Numerical Scheme with Newton Polynomial.
p.
1.

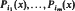 (where
(where 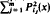 is bounded on the interval [ −
is bounded on the interval [ −