Article contents
A note on the correlation of classes
Published online by Cambridge University Press: 20 January 2009
Extract
Let R be a (1 — 1) relation between the members of two similar classes A, B1. It correlates the members of a subclass X of A to the members of a certain subclass Y of B1 and thus defines a relation ρ connecting X and Y. It is clear that ρ is a (1 – 1) relation and that it has the property (M). If X1ρ Y1, X2ρY2, then 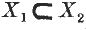 implies
implies 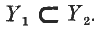
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1927
References
page 47 note 1 There may be no L's, but this does not matter since the null class is counted as a subclass of A. It will be noticed that the proof depends only on the fact that ρ. σ are (1 – 1 ) relations with the property (M), so that the theorem is true for any relations with these properties. Thus it is not necessary that the members of X should be in (1 – 1) relation with those of Y, nor that those subclasses of B to which the subclasses of A are correlated by ρ should be all the subclasses of a certain part B1 of B.
page 48 note 1 i.e. if a, b are cardinal numbers, a ≤ b and b ≤ a together imply a = b.
- 3
- Cited by

