No CrossRef data available.
Article contents
On a generalisation of a result of Ramanujan connected with the exponential series
Published online by Cambridge University Press: 20 January 2009
Extract
One of the many interesting problems discussed by Ramanujan is an approximation related to the exponential series for en, when n assumes large positive integer values. If the number θn is defined by
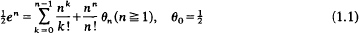
Ramanujan (9) showed that when n is large, θn possesses the asymptotic expansion
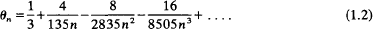
The first demonstrations that θn lies between ½ and 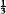 and that θn decreases monotoni-cally to the value
and that θn decreases monotoni-cally to the value 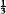 as n increases, were given by Szegö (12) and Watson (13). Analogous results were shown to exist for the function e−n, for positive integer values of n, by Copson (4). If φn is defined by
as n increases, were given by Szegö (12) and Watson (13). Analogous results were shown to exist for the function e−n, for positive integer values of n, by Copson (4). If φn is defined by
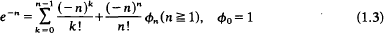
then πn lies between 1 and ½ and tends monotonically to the value ½ as n increases, with the asymptotic expansion
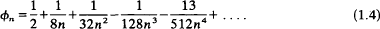
A generalisation of these results was considered by Buckholtz (2) who defined, in a slightly different notation, for complex z and positive integer n, the function φn(z) by
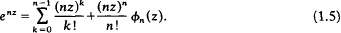
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 24 , Issue 3 , October 1981 , pp. 179 - 195
- Copyright
- Copyright © Edinburgh Mathematical Society 1981


