Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T06:29:36.234Z Has data issue: false hasContentIssue false
  • English
  • Français

On Central Series

Published online by Cambridge University Press:  20 January 2009

I. D. Macdonald
I. D. Macdonald
Affiliation:
Department of Mathematics, Institute of Advanced Studies, Australian National University, Canberra
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let

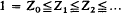
and

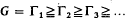
be, respectively, the upper and lower central series of a group G. Our purpose in this note is to extend known results and find some information as to which of the factors Zk/Zk−1 and Γk/Γk+1 may be infinite. Though our conclusions about the lower central series will be quite general we assume in the other case that the group is f.n., i.e. an extension of a finite group by a nilpotent group. The essential facts about f.n. groups are to be found in P. Hall's paper (4). We also refer to (4) for general notation; we reserve the letter k for positive integers.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 13 , Issue 2 , December 1962 , pp. 175 - 178
Copyright
Copyright © Edinburgh Mathematical Society 1962

References

(1) Baer, R., Representations of groups as quotient groups, Trans. Anier. Math. Soc., 58 (1945), 295–419.Google Scholar
(2) Baer, R., Endlichkeitskriterien für Kommutatorgruppen, Math. Annalen, 124 1952), 161–177.CrossRefGoogle Scholar
(3) Baer, R., Finite extensions: of abelian groups with minimum condition, Trans. Amer. Math. Soc., 79 (1955), 521–540.CrossRefGoogle Scholar
(4) Hall, P., Finite-by-nilpotent groups, Proc. Camb. Phil. Soc., 52 (1956), 611–616.CrossRefGoogle Scholar
(5) Macdonald, I. D., On certain varieties of groups, Math. Zeit., 76 (1961), 270–282.CrossRefGoogle Scholar