Article contents
On holomorphic reflexivity conditions for complex Lie groups
Published online by Cambridge University Press: 30 September 2021
Abstract
We consider Akbarov's holomorphic version of the non-commutative Pontryagin duality for a complex Lie group. We prove, under the assumption that $G$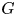 is a Stein group with finitely many components, that (1) the topological Hopf algebra of holomorphic functions on $G$
is a Stein group with finitely many components, that (1) the topological Hopf algebra of holomorphic functions on $G$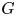 is holomorphically reflexive if and only if $G$
is holomorphically reflexive if and only if $G$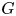 is linear; (2) the dual cocommutative topological Hopf algebra of exponential analytic functional on $G$
is linear; (2) the dual cocommutative topological Hopf algebra of exponential analytic functional on $G$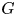 is holomorphically reflexive. We give a counterexample, which shows that the first criterion cannot be extended to the case of infinitely many components. Nevertheless, we conjecture that, in general, the question can be solved in terms of the Banach-algebra linearity of $G$
is holomorphically reflexive. We give a counterexample, which shows that the first criterion cannot be extended to the case of infinitely many components. Nevertheless, we conjecture that, in general, the question can be solved in terms of the Banach-algebra linearity of $G$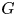 .
.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 64 , Issue 4 , November 2021 , pp. 800 - 821
- Copyright
- Copyright © The Author(s), 2021. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society
References
- 6
- Cited by


