Published online by Cambridge University Press: 20 January 2009
Kilmister (1) has considered dynamical systems specified by coordinates q( = 1, 2, , n) and a Lagrangian
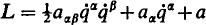
(with summation convention). He sought to determine generally covariant conditions for the existence of a first integral, 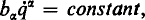 , linear in the velocities. He showed that it is not, as is usually stated, necessary that there must exist an ignorable coordinate (equivalently, that b must be a Killing field:
, linear in the velocities. He showed that it is not, as is usually stated, necessary that there must exist an ignorable coordinate (equivalently, that b must be a Killing field:
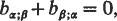
where covariant derivation is with respect to a). On the contrary, a singular integral, in the sense that 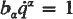 for all time if satisfied initially, need not be accompanied by an ignorable coordinate.
for all time if satisfied initially, need not be accompanied by an ignorable coordinate.