Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-10T21:17:13.158Z Has data issue: false hasContentIssue false
  • English
  • Français

On minimal log discrepancies and kollár components

Part of: Local theory Birational geometry

Published online by Cambridge University Press:  04 November 2021

Joaquín Moraga
Joaquín Moraga*
Affiliation:
Department of Mathematics, University of Utah, 155 S 1400 E, JWB 321, Salt Lake City, UT 84112, USA (moraga@math.utah.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article, we prove a local implication of boundedness of Fano varieties. More precisely, we prove that $d$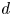-dimensional $a$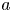-log canonical singularities with standard coefficients, which admit an $\epsilon$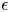-plt blow-up, have minimal log discrepancies belonging to a finite set which only depends on $d,\,a$ 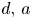and $\epsilon$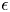. This result gives a natural geometric stratification of the possible mld's in a fixed dimension by finite sets. As an application, we prove the ascending chain condition for minimal log discrepancies of exceptional singularities. We also introduce an invariant for klt singularities related to the total discrepancy of Kollár components.

Keywords

log terminalKollar componentslog discrepancies

MSC classification

Primary: 14E30: Minimal model program (Mori theory, extremal rays)
Secondary: 14B05: Singularities
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 64 , Issue 4 , November 2021 , pp. 982 - 1001
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alexeev, V., Two two-dimensional terminations, Duke Math. J. 69(3) (1993), 527–545, doi:10.1215/S0012-7094-93-06922-0, MR1208810 $\uparrow$2.CrossRefGoogle Scholar
Alexeev, V., Boundedness and K2 for log surfaces, Internat. J. Math. 5(6) (1994), 779–810, doi:10.1142/S0129167X94000395, MR1298994 $\uparrow$7.CrossRefGoogle Scholar
Ambro, F., On minimal log discrepancies, Math. Res. Lett. 6(5-6) (1999), 573–580, doi:10.4310/MRL.1999.v6.n5.a10, MR1739216 $\uparrow$2.CrossRefGoogle Scholar
Ambro, F., The set of toric minimal log discrepancies, Cent. Eur. J. Math. 4(3) (2006), 358–370, doi:10.2478/s11533-006-0013-x, MR2233855 $\uparrow$2.CrossRefGoogle Scholar
Ambro, F., Basic properties of log canonical centers, classification of algebraic varieties, EMS Ser. Congr. Rep., Eur. Math. Soc. Zürich 366 (2011), 39–48, doi:10.4171/007-1/2, MR2779466 $\uparrow$10.Google Scholar
Birkar, C., Singularities of linear systems and boundedness of Fano varieties, 2016 https://arxiv.org/abs/1609.05543v1. $\uparrow$2, 3, 8, 13.Google Scholar
Birkar, C., Anti-pluricanonical systems on Fano varieties, Ann. Math. (2) 190(2) (2019), 345–463, doi:10.4007/annals.2019.190.2.1, MR3997127 $\uparrow$1, 4, 6, 8, 9, 13.CrossRefGoogle Scholar
Borisov, A., Minimal discrepancies of toric singularities, Manuscripta Math. 92(1) (1997), 33–45, doi:10.1007/BF02678179, MR1427666 $\uparrow$2CrossRefGoogle Scholar
de Fernex, T., Ein, L. and Mustaţă, M., Shokurov's ACC conjecture for log canonical thresholds on smooth varieties, Duke Math. J. 152(1) (2010), 93–114, doi:10.1215/00127094-2010-008, MR2643057 $\uparrow$1.CrossRefGoogle Scholar
de Fernex, T., Kollár, J. and Xu, C., The dual complex of singularities, Higher dimensional algebraic geometry – in honour of Professor Yujiro Kawamata's sixtieth birthday, Adv. Stud. Pure Math., Volume 74, pp. 103–129 (Math. Soc. Japan, Tokyo, 2017). MR3791210 $\uparrow$1.Google Scholar
Filipazzi, S. and Moraga, J., Strong ($\delta,\,n$)-complements for semi-stable morphisms, 2018. https://arxiv.org/abs/1810.01990. $\uparrow$9, 11.Google Scholar
Fujino, O., The indices of log canonical singularities, Amer. J. Math. 123(2) (2001), 229–253. MR1828222 $\uparrow$3, 11, 13.CrossRefGoogle Scholar
Hacon, C. D., On the log canonical inversion of adjunction, Proc. Edinb. Math. Soc. (2) 57(1) (2014), 139–143, doi:10.1017/S0013091513000837, MR3165017 $\uparrow$2.CrossRefGoogle Scholar
Hayakawa, T., Blowing ups of 3-dimensional terminal singularities, Publ. Res. Inst. Math. Sci. 35(3) (1999), 515–570, doi:10.2977/prims/1195143612, MR1710753 $\uparrow$13.CrossRefGoogle Scholar
Hacon, C. D. and Kovács, S. J., Classification of higher dimensional algebraic varieties, Oberwolfach Seminars, Volume 41 (Birkhäuser Verlag, Basel, 2010). MR2675555 $\uparrow$8.CrossRefGoogle Scholar
Hacon, C. D., McKernan, J. and Xu, C., ACC for log canonical thresholds, Ann. Math. (2) 180(2) (2014), 523–571, doi:10.4007/annals.2014.180.2.3, MR3224718 $\uparrow$1.CrossRefGoogle Scholar
Han, J., Liu, J. and Shokurov, V. V., Boundedness of singularities admitting an $\epsilon$-PLT blow-up, 2019. $\uparrow$3Google Scholar
Ishii, S., The quotients of log-canonical singularities by finite groups, Singularities – Sapporo 1998, Adv. Stud. Pure Math., Volume 29, pp. 135–161 (Kinokuniya, Tokyo, 2000). MR1819634 $\uparrow$3.Google Scholar
Ishii, S. and Prokhorov, Y., Hypersurface exceptional singularities, Internat. J. Math. 12(6) (2001), 661–687, doi:10.1142/S0129167X0100099X, MR1875648 $\uparrow$3.CrossRefGoogle Scholar
Kawamata, Y., Matsuda, K. and Matsuki, K., Introduction to the minimal model problem, Algebraic geometry, Sendai, 1985, Adv. Stud. Pure Math., Vol. 10 (North-Holland, Amsterdam, 1987), pp. 283–360. MR946243 $\uparrow$12Google Scholar
Kollár, J., Effective base point freeness, Math. Ann. 296(4) (1993), 595–605, doi:10.1007/BF01445123, MR1233485 $\uparrow$7.CrossRefGoogle Scholar
Kollár, J., Singularities of the minimal model program, Cambridge Tracts in Mathematics, Volume 200 (Cambridge University Press, Cambridge, 2013). With a collaboration of S. Kovács. MR3057950 $\uparrow$1, 14.Google Scholar
Kollár, J., New examples of terminal and log canonical singularities, 2016. https://arxiv.org/abs/1107.2864. $\uparrow$1.Google Scholar
Kollár, J. and Kovács, S. J., Log canonical singularities are Du Bois, J. Amer. Math. Soc. 23(3) (2010), 791–813, doi:10.1090/S0894-0347-10-00663-6, MR2629988 $\uparrow$5.CrossRefGoogle Scholar
Kollár, J. and Mori, S., Birational geometry of algebraic varieties, Cambridge Tracts in Mathematics, Vol. 134 (Cambridge University Press, Cambridge, 1998). With the collaboration of C. H. Clemens and A. Corti; Translated from the 1998 Japanese original. MR1658959 $\uparrow$4, 5, 9, 10.Google Scholar
Kollár, J. and Xu, C., The dual complex of Calabi-Yau pairs, Invent. Math. 205(3) (2016), 527–557, doi:10.1007/s00222-015-0640-6, MR3539921 $\uparrow$1.CrossRefGoogle Scholar
Li, C., K-semistability is equivariant volume minimization, Duke Math. J. 166(16) (2017), 3147–3218, doi:10.1215/00127094-2017-0026, MR3715806 $\uparrow$1.CrossRefGoogle Scholar
Li, C. and Xu, C., Stability of valuations: higher rational rank, 2017. https://arxiv.org/abs/1707.05561. $\uparrow$1, 4.Google Scholar
Li, C. and Xu, C., Stability of valuations and Kollár components, J. Eur. Math. Soc. (JEMS) 22(8) (2020), 2573–2627, doi:10.4171/JEMS/972, MR4118616 $\uparrow$1.CrossRefGoogle Scholar
Markushevich, D. and Prokhorov, Yu. G., Exceptional quotient singularities, Amer. J. Math. 121(6) (1999), 1179–1189, MR1719826 $\uparrow$3, 5.CrossRefGoogle Scholar
Prokhorov, Y. G. and Shokurov, V. V., The first fundamental theorem on complements: from global to local, Izv. Ross. Akad. Nauk Ser. Mat. 65(6) (2001), 99–128, doi:10.1070/IM2001v065n06ABEH000366, Math. 65 (2001), no. 6, 1169–1196. MR1892905 $\uparrow$1, 3.Google Scholar
Prokhorov, Y. G. and Shokurov, V. V., Towards the second main theorem on complements, J. Algebraic Geom. 18(1) (2009), 151–199, doi:10.1090/S1056-3911-08-00498-0, MR2448282 $\uparrow$1.CrossRefGoogle Scholar
Shokurov, V. V., A supplement to: “Three-dimensional log perestroikas”, Izv. Ross. Akad. Nauk Ser. Mat. 57(6) (1993), 141–175, doi:10.1070/IM1994v043n03ABEH001579, [Izv. Ross. Akad. Nauk Ser. Mat. 56 (1992) no. 1, 105–203; MR1162635 (93j:14012)], Sci. Izv. Math. 43 (1994), no. 3, 527–558. MR1256571 $\uparrow$8, 9.Google Scholar
Shokurov, V. V., 3-fold log models, J. Math. Sci. 81(3) (1996), 2667–2699, doi:10.1007/BF02362335, Algebraic geometry, 4. MR1420223 $\uparrow$2.CrossRefGoogle Scholar
Shokurov, V. V., Complements on surfaces, J. Math. Sci. (New York) 102(2) (2000), 3876–3932, doi:10.1007/BF02984106, Algebraic geometry, 10. MR1794169 $\uparrow$2, 3.CrossRefGoogle Scholar
Shokurov, V. V., Letters of a bi-rationalist. V. Minimal log discrepancies and termination of log ips, Tr. Mat. Inst. Steklova 246 (2004), 184–208, Algebr. Geom. Metody, Svyazi i Prilozh., 328–351 (Russian, with Russian summary); English transl., Proc. Steklov Inst. Math. 3(246) (2004), 315–336. MR2101303 $\uparrow$2.Google Scholar
Xu, C., Finiteness of algebraic fundamental groups, Compos. Math. 150(3) (2014), 409–414, doi:10.1112/S0010437X13007562, MR3187625 $\uparrow$1, 2, 5.CrossRefGoogle Scholar
Xu, C., Interaction between singularity theory and the minimal model program, Proceedings of the International Congress of Mathematicians – Rio de Janeiro. Volume II. Invited lectures, pp. 807–830 (World Scientific Publications, Hackensack, NJ, 2018). MR3966790 $\uparrow$1Google Scholar
Zariski, O., The reduction of the singularities of an algebraic surface, Ann. Math. (2) 40 (1939), 639–689. doi:10.2307/1968949. MR0000159 $\uparrow$10.CrossRefGoogle Scholar