Article contents
On minimal thinness, reduced functions and Green potentials
Published online by Cambridge University Press: 20 January 2009
Abstract
Let Ω be an open connected subset of the unit disc U, let E = U\Ω and let {Ωk} be a Whitney decomposition of U. If z(Q) is the centre of the “square” Q, if T is the unit circle and t = dist.(Q, T), we consider
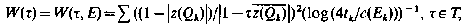
where Ek = E ∩ Qk and c(Ek) is the capacity of Ek. We prove that the set E is minimally thin at τ ∈ T in U if and only if W(τ)< ∞. We study functions of type W and discuss the relation between certain results of Naim on minimal thinness [15], a minimum principle of Beurling [3], related results due to Dahlberg [7] and Sjögren [16] and recent work of Hayman-Lyons [15] (cf. also Bonsall [4]) and Volberg [19]. For simplicity, we discuss our problems in the unit disc U in the plane. However, the same techniques work for analogous problems in higher dimensions and in more complicated regions.
Information
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 36 , Issue 1 , February 1993 , pp. 87 - 106
- Copyright
- Copyright © Edinburgh Mathematical Society 1993
References
REFERENCES
- 11
- Cited by

