No CrossRef data available.
Article contents
On some fractional integrals and their applications
Published online by Cambridge University Press: 20 January 2009
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
In previous papers [3, 4] the author has discussed the symmetric generalised Erdélyi–Kober operators of fractional integration defined by
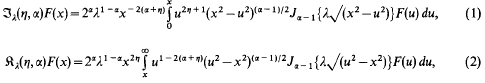
where α>0, γ≧0 and the operators ℑiγ(η,α) and 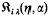 defined as in equations (1) and (2) respectively but with Jα−1, the Bessel function of the first kind replaced by Iα−1, the modified Bessel function of the first kind.
defined as in equations (1) and (2) respectively but with Jα−1, the Bessel function of the first kind replaced by Iα−1, the modified Bessel function of the first kind.
Information
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 28 , Issue 1 , February 1985 , pp. 97 - 105
- Copyright
- Copyright © Edinburgh Mathematical Society 1985
References
REFERENCES
1.Gilbert, R. P., Function theoretic methods in partial differential equations (Academic Press, 1969).Google Scholar
2.Lowndes, J. S., Parseval relations for Kontorovich-Lebedev transforms, Proc. Edinburgh Math.Soc. 13 (1962), 5–11.CrossRefGoogle Scholar
3.Lowndes, J. S., A generalisation of the Erdélyi–Kober operators, Proc. Edinburgh Math. Soc. 17 (1970), 139–148.CrossRefGoogle Scholar
4.Lowndes, J. S., An application of some fractional integrals, Glasgow Math. J. 20 (1979), 35–41.CrossRefGoogle Scholar
5.Magnus, W., Oberhettinger, F. and Soni, R. P., Formulas and theorems for the special functions of mathematical physics, 3rd ed. (Springer-Verlag, 1966).CrossRefGoogle Scholar

