No CrossRef data available.
Published online by Cambridge University Press: 20 January 2009
Strong summability has been studied by many authors, including Borwein and Cass (1, 2) who have studied sequence-to-sequence transforms. Here we studyintegral transforms; and due to the lack of a limitation theorem for such transforms, some results do not follow directly as in the sequence cases. The strong methods defined here can be applied to construct known and new strong summability methods. We do not give details here, but refer the reader to (3) with the suggestion that the natural scale operator method be used for Q and the named method for P. For example, with the Cesà methods, let P=(C,k,δ) and Q=(C,δ) to obtain 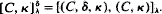 .
.