Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Chen, Zong-Xuan
and
Gao, Shi-An
2013.
THE FUNCTION ANALYTIC IN THE EXTERIOR OF A DISC AND ITS APPLICATION TO PERIODIC COMPLEX OSCILLATION.
Bulletin of the Korean Mathematical Society,
Vol. 50,
Issue. 5,
p.
1415.

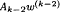 + … +
+ … + 