1. Introduction
Let ![]() $\mathbb{F}$ be the field of complex numbers or the skew field
$\mathbb{F}$ be the field of complex numbers or the skew field ![]() ${\mathbb{H}}$ of Hamilton quaternions. Let
${\mathbb{H}}$ of Hamilton quaternions. Let ![]() $\mathcal{H}$ be a Hilbert space over
$\mathcal{H}$ be a Hilbert space over ![]() $\mathbb{F}$ and let T be a bounded linear operator on
$\mathbb{F}$ and let T be a bounded linear operator on ![]() $\mathcal{H}$. The numerical range of T is the set
$\mathcal{H}$. The numerical range of T is the set
where ![]() $\langle \cdot\,,\cdot\,\rangle:\mathcal{H}\times\mathcal{H}\to\mathbb{F}$ is the inner product on
$\langle \cdot\,,\cdot\,\rangle:\mathcal{H}\times\mathcal{H}\to\mathbb{F}$ is the inner product on ![]() $\mathcal{H}$. This subset of
$\mathcal{H}$. This subset of ![]() $\mathbb{F}$ was introduced and studied by Toeplitz in 1918, who proved that, when
$\mathbb{F}$ was introduced and studied by Toeplitz in 1918, who proved that, when ![]() ${\mathbb{F}}={\mathbb{C}}$, the outer boundary of W(T) is a convex curve and conjectured that the whole numerical range was convex, see [Reference Toeplitz14]. Shortly after, in 1919, Hausdorff [Reference Hausdorff10] proved the conjecture. Since then, this result is known as the Toeplitz–Hausdorff theorem.
${\mathbb{F}}={\mathbb{C}}$, the outer boundary of W(T) is a convex curve and conjectured that the whole numerical range was convex, see [Reference Toeplitz14]. Shortly after, in 1919, Hausdorff [Reference Hausdorff10] proved the conjecture. Since then, this result is known as the Toeplitz–Hausdorff theorem.
Over the years, the investigation of the numerical range continuously increased, including the cases of linear operators on infinite dimensional complex Hilbert spaces and complex Banach spaces. In 1951, Kippenhahn [Reference Kippenhahn and Hochstenbach16] introduced the study of numerical range for quaternionic operators, i.e. when ![]() ${\mathbb{F}}={\mathbb{H}}$. Soon it became evident that, although sharing many properties of its complex counterpart, the quaternionic numerical range was no longer always convex.
${\mathbb{F}}={\mathbb{H}}$. Soon it became evident that, although sharing many properties of its complex counterpart, the quaternionic numerical range was no longer always convex.
The bild of an operator T, also introduced in [Reference Kippenhahn and Hochstenbach16], is the intersection ![]() $B(T)=W_{\mathbb{H}}(T)\cap{\mathbb{C}}$. Since every quaternion is, up to unitary equivalence, a complex number, many properties of the numerical range are encoded in the bild, including convexity. In fact,
$B(T)=W_{\mathbb{H}}(T)\cap{\mathbb{C}}$. Since every quaternion is, up to unitary equivalence, a complex number, many properties of the numerical range are encoded in the bild, including convexity. In fact, ![]() $W_{\mathbb{H}}(T)$ is convex if, and only if, B(T) is convex, see [Reference Carvalho, Diogo and Mendes3]. However, the upper bild
$W_{\mathbb{H}}(T)$ is convex if, and only if, B(T) is convex, see [Reference Carvalho, Diogo and Mendes3]. However, the upper bild ![]() $B^+(T)$, which is the intersection of
$B^+(T)$, which is the intersection of ![]() $W_{\mathbb{H}}(T)$ with the closure of the upper half-plane, is always convex.
$W_{\mathbb{H}}(T)$ with the closure of the upper half-plane, is always convex.
The pursuit of convexity remained an important issue in the quaternionic setting, with Au-Yeung establishing in [Reference Au-Yeung15] necessary and sufficient conditions for ![]() $W_{\mathbb{H}}(T)$ to be convex.
$W_{\mathbb{H}}(T)$ to be convex.
In a series of recent papers [Reference Carvalho, Diogo and Mendes1], [Reference Carvalho, Diogo and Mendes2], [Reference Carvalho, Diogo and Mendes3], [Reference Carvalho, Diogo and Mendes4], [Reference Carvalho, Diogo and Mendes5], the convexity and shape of the numerical range of quaternionic matrices have been studied by the first three named authors. The notion of S-spectrum (see [Reference Colombo, Gantner and Kimsey8, Reference Colombo, Sabadini and Struppa9]) and its relation with the numerical range on infinite dimensional quaternionic Hilbert spaces was addressed in the recent paper [Reference Carvalho, Diogo and Mendes6]. Another geometric object in the realm of infinite dimensional Hilbert spaces is the essential numerical range of an operator T. It is defined as the set
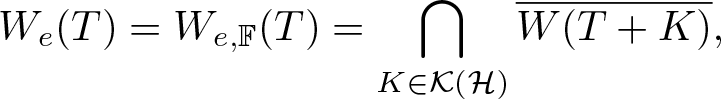 \begin{equation*}
W_{e}(T)=W_{e,{\mathbb{F}}}(T)=\bigcap_{K\in{\mathcal{K}}({\mathcal{H}})}\overline{W(T+K)},
\end{equation*}
\begin{equation*}
W_{e}(T)=W_{e,{\mathbb{F}}}(T)=\bigcap_{K\in{\mathcal{K}}({\mathcal{H}})}\overline{W(T+K)},
\end{equation*} where ![]() $\mathcal{K}(\mathcal{H})$ denotes the set of compact operators on the
$\mathcal{K}(\mathcal{H})$ denotes the set of compact operators on the ![]() ${\mathbb{F}}$-Hilbert space
${\mathbb{F}}$-Hilbert space ![]() $\mathcal{H}$. Taking K to be the zero operator in the above definition, we see that
$\mathcal{H}$. Taking K to be the zero operator in the above definition, we see that  $W_{e,{\mathbb{F}}}(T)\subseteq\overline{W_{\mathbb{F}}(T)}$.
$W_{e,{\mathbb{F}}}(T)\subseteq\overline{W_{\mathbb{F}}(T)}$.
This paper is devoted to the study of the essential numerical range in the quaternionic setting. The main result is Theorem 4.2 where we show that, for ![]() ${\mathbb{F}}={\mathbb{H}}$, the essential numerical range
${\mathbb{F}}={\mathbb{H}}$, the essential numerical range ![]() $W_{e}(T)=W_{e,{\mathbb{H}}}(T)$ is always a convex set. Thus, at least convexity of this essential part of the numerical range is guaranteed even in the quaternionic setting. We emphasize that this is a surprising and unexpected result since the essential numerical range is the intersection of non-convex sets and nothing indicates it is convex in its formulation.
$W_{e}(T)=W_{e,{\mathbb{H}}}(T)$ is always a convex set. Thus, at least convexity of this essential part of the numerical range is guaranteed even in the quaternionic setting. We emphasize that this is a surprising and unexpected result since the essential numerical range is the intersection of non-convex sets and nothing indicates it is convex in its formulation.
To secure this result, we use a general property (Lemma 4.1): given a pair of unitary sequences  $x_n^{(1)}, x_n^{(2)}$ and
$x_n^{(1)}, x_n^{(2)}$ and ![]() $T\in {\mathcal{B}}({\mathcal{H}})$, a judicious choice of N and M shows that the following vectors are close to orthogonal
$T\in {\mathcal{B}}({\mathcal{H}})$, a judicious choice of N and M shows that the following vectors are close to orthogonal
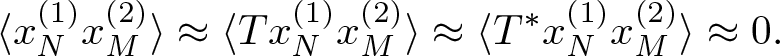 \begin{equation*}
\langle{x^{(1)}_N}{x^{(2)}_M}\rangle \approx \langle{Tx^{(1)}_N}{x^{(2)}_M}\rangle \approx \langle{T^*x^{(1)}_N}{x^{(2)}_M}\rangle\approx 0.
\end{equation*}
\begin{equation*}
\langle{x^{(1)}_N}{x^{(2)}_M}\rangle \approx \langle{Tx^{(1)}_N}{x^{(2)}_M}\rangle \approx \langle{T^*x^{(1)}_N}{x^{(2)}_M}\rangle\approx 0.
\end{equation*} We can then form an essential sequence (see Definition 3.3) for the convex combination ![]() $\alpha^2 \omega^{(1)}+\beta^2\omega^{(2)}$,
$\alpha^2 \omega^{(1)}+\beta^2\omega^{(2)}$, ![]() $\omega^{(1)}, \omega^{2}\in W_e(T)$, with elements of the form
$\omega^{(1)}, \omega^{2}\in W_e(T)$, with elements of the form  $\alpha x_N^{(1)}+\beta x^{(2)}_M$. The referred quasi orthogonality implies that
$\alpha x_N^{(1)}+\beta x^{(2)}_M$. The referred quasi orthogonality implies that
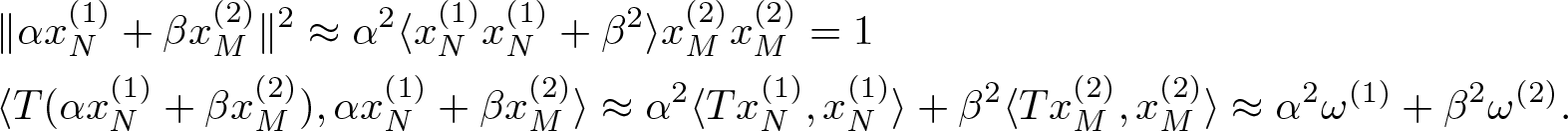 \begin{align*}
&\|\alpha x_N^{(1)}+\beta x_M^{(2)}\|^2\approx \alpha^2\langle{x_N^{(1)}}{x_N^{(1)}}+\beta^2 \rangle{x_M^{(2)}}{x_M^{(2)}}=1\\
&\langle T(\alpha x_N^{(1)}+\beta x_M^{(2)}), \alpha x_N^{(1)}+\beta x_M^{(2)}\rangle\approx \alpha^2\langle T x_N^{(1)}, x_N^{(1)}\rangle+\beta^2 \langle T x_M^{(2)}, x_M^{(2)}\rangle\approx \alpha^2 \omega^{(1)}+\beta^2\omega^{(2)}.
\end{align*}
\begin{align*}
&\|\alpha x_N^{(1)}+\beta x_M^{(2)}\|^2\approx \alpha^2\langle{x_N^{(1)}}{x_N^{(1)}}+\beta^2 \rangle{x_M^{(2)}}{x_M^{(2)}}=1\\
&\langle T(\alpha x_N^{(1)}+\beta x_M^{(2)}), \alpha x_N^{(1)}+\beta x_M^{(2)}\rangle\approx \alpha^2\langle T x_N^{(1)}, x_N^{(1)}\rangle+\beta^2 \langle T x_M^{(2)}, x_M^{(2)}\rangle\approx \alpha^2 \omega^{(1)}+\beta^2\omega^{(2)}.
\end{align*} We finish the paper with Theorem 4.3, where we prove a quaternionic version of Lancaster theorem relating the numerical range and the essential numerical range, see [Reference Lancaster11]. Due to the non-convexity of the numerical range, we need to introduce the notion of inter-convex hull (see 4.7). The result asserts that the closure of the quaternionic numerical range is precisely the inter-convex hull of the quaternionic essential numerical range and the quaternionic numerical range, i.e. ![]() $\overline{W(T)}={{\rm iconv\,}}\{W_e(T), W(T)\}$. In spite of the formal similarities with its complex counterpart, there are worth mentioning differences. Foremost we can not infer that the numerical range is closed when it contains the essential numerical range (see Remark 4.5) as in complex Hilbert spaces [Reference Lancaster11, Corollary 1]. This is because the quaternionic numerical range lacks convexity and the quaternionic Lancaster theorem uses the weaker notion of inter-convex hull. In addition, Remark 4.5 tells us that, even though the upper bild is convex, we still do not recover Lancaster theorem in its complex form.
$\overline{W(T)}={{\rm iconv\,}}\{W_e(T), W(T)\}$. In spite of the formal similarities with its complex counterpart, there are worth mentioning differences. Foremost we can not infer that the numerical range is closed when it contains the essential numerical range (see Remark 4.5) as in complex Hilbert spaces [Reference Lancaster11, Corollary 1]. This is because the quaternionic numerical range lacks convexity and the quaternionic Lancaster theorem uses the weaker notion of inter-convex hull. In addition, Remark 4.5 tells us that, even though the upper bild is convex, we still do not recover Lancaster theorem in its complex form.
2. Notation and preliminaries
The division ring of real quaternions ![]() ${\mathbb{H}}$, also known as Hamilton quaternions, is an algebra over the field of real numbers with basis
${\mathbb{H}}$, also known as Hamilton quaternions, is an algebra over the field of real numbers with basis ![]() $\{1,i,j,k\}$ and product defined by
$\{1,i,j,k\}$ and product defined by ![]() $i^2=j^2=k^2=ijk=-1$. Given a quaternion
$i^2=j^2=k^2=ijk=-1$. Given a quaternion ![]() $q=q_0+q_1i+q_2j+q_3k$, its conjugate is
$q=q_0+q_1i+q_2j+q_3k$, its conjugate is ![]() $q^*=q_0-q_1i-q_2j-q_3k$. We call
$q^*=q_0-q_1i-q_2j-q_3k$. We call  ${{\rm Re\,}}(q)=\frac{q+q^*}{2}$ and
${{\rm Re\,}}(q)=\frac{q+q^*}{2}$ and  ${{\rm Im\,}}(q)=\frac{q-q^*}{2}$ the real and imaginary parts of q, respectively. The norm of q is the non-negative real number
${{\rm Im\,}}(q)=\frac{q-q^*}{2}$ the real and imaginary parts of q, respectively. The norm of q is the non-negative real number ![]() $|q|=\sqrt{qq^*}$. Two quaternions
$|q|=\sqrt{qq^*}$. Two quaternions ![]() $q,q'\in{\mathbb{H}}$ are similar if there is a unitary
$q,q'\in{\mathbb{H}}$ are similar if there is a unitary ![]() $u\in{\mathbb{H}}$ such that
$u\in{\mathbb{H}}$ such that ![]() $u^*qu=q'$, in which case we write
$u^*qu=q'$, in which case we write ![]() $q\sim q'$. This is an equivalence relation and we denote the equivalence class of q by
$q\sim q'$. This is an equivalence relation and we denote the equivalence class of q by ![]() $[q]$.
$[q]$.
Let ![]() $\mathcal{H}$ denote an infinite dimensional two-sided Hilbert space over
$\mathcal{H}$ denote an infinite dimensional two-sided Hilbert space over ![]() ${\mathbb{H}}$. In particular, the norm of
${\mathbb{H}}$. In particular, the norm of ![]() $x\in\mathcal{H}$ is defined by the underlying
$x\in\mathcal{H}$ is defined by the underlying ![]() ${\mathbb{H}}$-inner product as
${\mathbb{H}}$-inner product as ![]() $\|x\|=\sqrt{\langle x,x\rangle}$. The inner product verifies the usual Cauchy–Schwartz inequality:
$\|x\|=\sqrt{\langle x,x\rangle}$. The inner product verifies the usual Cauchy–Schwartz inequality: ![]() $|\langle x,y\rangle|\leqslant\|x\|\|y\|$, for every
$|\langle x,y\rangle|\leqslant\|x\|\|y\|$, for every ![]() $x,y\in\mathcal{H}$. The space of bounded, right
$x,y\in\mathcal{H}$. The space of bounded, right ![]() ${\mathbb{H}}$-linear operators on
${\mathbb{H}}$-linear operators on ![]() $\mathcal{H}$ is denoted by
$\mathcal{H}$ is denoted by ![]() $\mathcal{B}(\mathcal{H})$, its closed ideal of compact operators by
$\mathcal{B}(\mathcal{H})$, its closed ideal of compact operators by ![]() $\mathcal{K}(\mathcal{H})$ and the group of invertible operators by
$\mathcal{K}(\mathcal{H})$ and the group of invertible operators by ![]() $\mathcal{B}(\mathcal{H})^{-1}$.
$\mathcal{B}(\mathcal{H})^{-1}$.
Every linear operator T considered in the text will be a bounded linear operator in ![]() $\mathcal{B}(\mathcal{H})$. Given
$\mathcal{B}(\mathcal{H})$. Given ![]() $q\in{\mathbb{H}}$ and
$q\in{\mathbb{H}}$ and ![]() $T \in \mathcal{B}(\mathcal{H})$, we define the operator
$T \in \mathcal{B}(\mathcal{H})$, we define the operator ![]() $\Delta_q(T):\mathcal{H}\to\mathcal{H}$ by
$\Delta_q(T):\mathcal{H}\to\mathcal{H}$ by
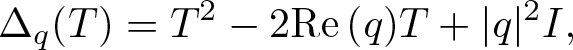 \begin{equation*}
\Delta_q(T)=T^2-2{{\rm Re\,}}(q)T+|q|^2I,
\end{equation*}
\begin{equation*}
\Delta_q(T)=T^2-2{{\rm Re\,}}(q)T+|q|^2I,
\end{equation*} where I is the identity operator. Clearly, ![]() $\Delta_q(T)\in\mathcal{B}(\mathcal{H})$. The S-spectrum is the set
$\Delta_q(T)\in\mathcal{B}(\mathcal{H})$. The S-spectrum is the set
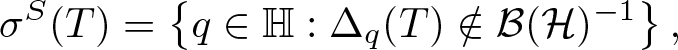 \begin{equation*}
\sigma^S(T)=\left\{q\in{\mathbb{H}}:\Delta_q(T)\notin \mathcal{B}(\mathcal{H})^{-1}\right\},
\end{equation*}
\begin{equation*}
\sigma^S(T)=\left\{q\in{\mathbb{H}}:\Delta_q(T)\notin \mathcal{B}(\mathcal{H})^{-1}\right\},
\end{equation*}which seems to be the appropriate notion for spectral analysis of linear operators on infinite dimensional quaternionic Hilbert spaces, see [Reference Colombo, Gantner and Kimsey8, Reference Colombo, Sabadini and Struppa9].
Let ![]() $\pi:{\mathcal{B}}({\mathcal{H}})\rightarrow {\mathcal{B}}({\mathcal{H}})/{\mathcal{K}}({\mathcal{H}})$ denote the canonical quotient map and
$\pi:{\mathcal{B}}({\mathcal{H}})\rightarrow {\mathcal{B}}({\mathcal{H}})/{\mathcal{K}}({\mathcal{H}})$ denote the canonical quotient map and ![]() ${\mathcal{C}}({\mathcal{H}})={\mathcal{B}}({\mathcal{H}})/{\mathcal{K}}({\mathcal{H}})$ the Calkin algebra. Let
${\mathcal{C}}({\mathcal{H}})={\mathcal{B}}({\mathcal{H}})/{\mathcal{K}}({\mathcal{H}})$ the Calkin algebra. Let ![]() $\pi(T)=[T]$ denote the equivalence class
$\pi(T)=[T]$ denote the equivalence class ![]() $T+{\mathcal{K}}({\mathcal{H}})$, for
$T+{\mathcal{K}}({\mathcal{H}})$, for ![]() $T\in {\mathcal{B}}({\mathcal{H}})$. Then
$T\in {\mathcal{B}}({\mathcal{H}})$. Then ![]() ${\mathcal{C}}({\mathcal{H}})$ is a normed algebra with
${\mathcal{C}}({\mathcal{H}})$ is a normed algebra with ![]() $\lVert [T]\rVert=\inf_{K\in{\mathcal{K}}({\mathcal{H}})}\lVert T+K\rVert \leqslant \lVert T\rVert$. We say that T is a Fredholm operator if the class
$\lVert [T]\rVert=\inf_{K\in{\mathcal{K}}({\mathcal{H}})}\lVert T+K\rVert \leqslant \lVert T\rVert$. We say that T is a Fredholm operator if the class ![]() $[T]$ is invertible in
$[T]$ is invertible in ![]() ${\mathcal{C}}({\mathcal{H}})$.
${\mathcal{C}}({\mathcal{H}})$.
According to Atkinson Theorem, ![]() $T\in {\mathcal{B}}({\mathcal{H}})$ is a Fredholm operator if and only if its range is closed and the kernels
$T\in {\mathcal{B}}({\mathcal{H}})$ is a Fredholm operator if and only if its range is closed and the kernels ![]() $\ker(T)$ and
$\ker(T)$ and ![]() $\ker(T^*)$ are finite dimensional, where
$\ker(T^*)$ are finite dimensional, where ![]() $T^*\in\mathcal{B}(\mathcal{H})$ is the adjoint of T. The set of all Fredholm operators in
$T^*\in\mathcal{B}(\mathcal{H})$ is the adjoint of T. The set of all Fredholm operators in ![]() ${\mathcal{B}}({\mathcal{H}})$ is denoted by
${\mathcal{B}}({\mathcal{H}})$ is denoted by ![]() ${\mathcal{F}}({\mathcal{H}})$.
${\mathcal{F}}({\mathcal{H}})$.
The essential S-spectrum of ![]() $T\in {\mathcal{B}}({\mathcal{H}})$ defined by
$T\in {\mathcal{B}}({\mathcal{H}})$ defined by
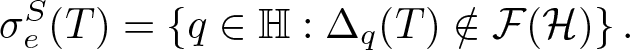 \begin{equation*}
\sigma_{e}^S(T)=\left\{q \in {\mathbb{H}}: \Delta_q(T) \notin {\mathcal{F}}({\mathcal{H}}) \right\}.
\end{equation*}
\begin{equation*}
\sigma_{e}^S(T)=\left\{q \in {\mathbb{H}}: \Delta_q(T) \notin {\mathcal{F}}({\mathcal{H}}) \right\}.
\end{equation*} is a non-empty compact subset of ![]() $\sigma^{S}(T)$, see [Reference Muraleetharan and Kengathram12].
$\sigma^{S}(T)$, see [Reference Muraleetharan and Kengathram12].
In the sequel, we will be working in the quaternion setting, that is, the quaternions ![]() ${\mathbb{H}}$ are our ground field (skew field to be more precise). Therefore, when we write W(T) or
${\mathbb{H}}$ are our ground field (skew field to be more precise). Therefore, when we write W(T) or ![]() $W_e(T)$, we always refer to the quaternionic numerical range or quaternionic essential numerical range.
$W_e(T)$, we always refer to the quaternionic numerical range or quaternionic essential numerical range.
Finally, define the essential bild and the essentials upper and lower bilds to be, respectively, ![]() $B_e(T)=W_e(T)\cap{\mathbb{C}}$,
$B_e(T)=W_e(T)\cap{\mathbb{C}}$, ![]() $B_e^+(T)=W_e(T)\cap{\mathbb{C}}^+$, and
$B_e^+(T)=W_e(T)\cap{\mathbb{C}}^+$, and ![]() $B_e^-(T)=W_e(T)\cap{\mathbb{C}}^-$, where
$B_e^-(T)=W_e(T)\cap{\mathbb{C}}^-$, where ![]() ${\mathbb{C}}^{\pm}$ is the closure of the respective half-planes.
${\mathbb{C}}^{\pm}$ is the closure of the respective half-planes.
3. Properties of the essential numerical range
This section is devoted to elementary properties of the essential numerical range and to prove some criteria for a quaternion to be in the essential numerical range of an operator. The results and their proofs are identical to the complex case with some adjustments. For the sake of completeness full proofs are provided. We start with an auxiliary result concerning compact operators.
Lemma 3.1. An operator T is compact if and only if ![]() $\langle Te_n,e_n\rangle\to 0$ for every orthonormal set
$\langle Te_n,e_n\rangle\to 0$ for every orthonormal set ![]() $(e_n)_{n}$.
$(e_n)_{n}$.
Proof. Let ![]() $T\in\mathcal{B}({\mathcal{H}})$ be compact and let
$T\in\mathcal{B}({\mathcal{H}})$ be compact and let ![]() $(e_n)_{n}$ be an orthonormal set. Let Pn be the projection onto
$(e_n)_{n}$ be an orthonormal set. Let Pn be the projection onto ![]() ${\text{span}\,}\{e_1,\dots, e_n\}$. Since T is compact, it is the limit of a sequence of finite rank operators, i.e.
${\text{span}\,}\{e_1,\dots, e_n\}$. Since T is compact, it is the limit of a sequence of finite rank operators, i.e. ![]() $\lim_{n\rightarrow\infty}\lVert P_nT-T\rVert=0$ (see [Reference Conway7, Corollary 4.5]). Then
$\lim_{n\rightarrow\infty}\lVert P_nT-T\rVert=0$ (see [Reference Conway7, Corollary 4.5]). Then
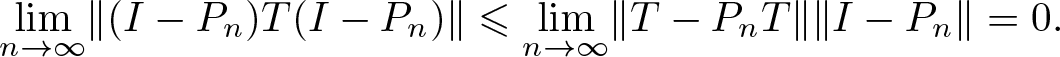 \begin{equation*}
\lim_{n\rightarrow\infty} \lVert (I-P_n)T(I-P_n)\rVert \leqslant\lim_{n\rightarrow\infty}\lVert T-P_nT\rVert \lVert I-P_n\rVert=0.
\end{equation*}
\begin{equation*}
\lim_{n\rightarrow\infty} \lVert (I-P_n)T(I-P_n)\rVert \leqslant\lim_{n\rightarrow\infty}\lVert T-P_nT\rVert \lVert I-P_n\rVert=0.
\end{equation*} Since ![]() $(I-P_n)e_{n+1}=e_{n+1}$, and using the Cauchy–Schwarz inequality, we have
$(I-P_n)e_{n+1}=e_{n+1}$, and using the Cauchy–Schwarz inequality, we have
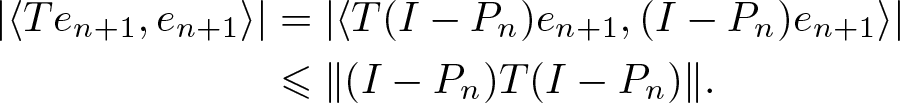 \begin{eqnarray*}
\lvert \langle T e_{n+1}, e_{n+1}\rangle\rvert &=& \lvert \langle T(I-P_n) e_{n+1}, (I-P_n)e_{n+1}\rangle \rvert\\
&\leqslant & \lVert (I-P_n)T(I-P_n)\rVert.
\end{eqnarray*}
\begin{eqnarray*}
\lvert \langle T e_{n+1}, e_{n+1}\rangle\rvert &=& \lvert \langle T(I-P_n) e_{n+1}, (I-P_n)e_{n+1}\rangle \rvert\\
&\leqslant & \lVert (I-P_n)T(I-P_n)\rVert.
\end{eqnarray*} Hence, ![]() $\langle T e_{n}, e_{n}\rangle\to 0$.
$\langle T e_{n}, e_{n}\rangle\to 0$.
For the converse, suppose that ![]() $T\in {\mathcal{B}}({\mathcal{H}})$ is such that
$T\in {\mathcal{B}}({\mathcal{H}})$ is such that ![]() $\langle T e_{n}, e_{n}\rangle\to 0$, for every orthonormal set
$\langle T e_{n}, e_{n}\rangle\to 0$, for every orthonormal set ![]() $(e_n)_{n}$. From
$(e_n)_{n}$. From ![]() $\Vert T \Vert = {\rm sup}_{\Vert x \Vert = \Vert y \Vert = 1} |\langle T_{x, y} \rangle|$, there exist unit vectors
$\Vert T \Vert = {\rm sup}_{\Vert x \Vert = \Vert y \Vert = 1} |\langle T_{x, y} \rangle|$, there exist unit vectors ![]() $x_1,y_1\in{\mathcal{H}}$ such that
$x_1,y_1\in{\mathcal{H}}$ such that
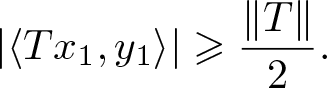 \begin{equation*}
\lvert \langle Tx_1,y_1\rangle \rvert\geqslant\frac{\lVert T\rVert }{2}.
\end{equation*}
\begin{equation*}
\lvert \langle Tx_1,y_1\rangle \rvert\geqslant\frac{\lVert T\rVert }{2}.
\end{equation*} A straightforward computation shows the following ‘polarization identity’, for all ![]() $x,y\in{\mathcal{H}}$:
$x,y\in{\mathcal{H}}$:
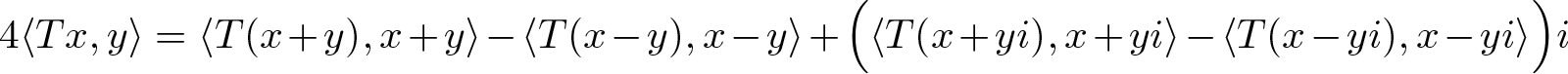 \begin{equation*}
4\langle Tx,y\rangle = {} \langle T(x+y), x+y \rangle-\langle T(x-y), x-y \rangle + \Big(\langle T(x+yi), x+yi \rangle- \langle T(x-yi), x-yi \rangle\Big)i
\end{equation*}
\begin{equation*}
4\langle Tx,y\rangle = {} \langle T(x+y), x+y \rangle-\langle T(x-y), x-y \rangle + \Big(\langle T(x+yi), x+yi \rangle- \langle T(x-yi), x-yi \rangle\Big)i
\end{equation*} \begin{equation*}
+k \Big(\langle T(x+yk), x+yk \rangle- \langle T(x-yk), x-yk \rangle\Big) + k \Big(\langle T(x+yj), x+yj \rangle- \langle T(x-yj), x-yj \rangle\Big)i .
\end{equation*}
\begin{equation*}
+k \Big(\langle T(x+yk), x+yk \rangle- \langle T(x-yk), x-yk \rangle\Big) + k \Big(\langle T(x+yj), x+yj \rangle- \langle T(x-yj), x-yj \rangle\Big)i .
\end{equation*}In particular, it follows that
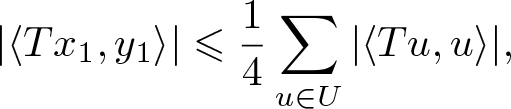 \begin{equation*}
|\langle Tx_1,y_1\rangle|\leqslant \frac{1}{4} \sum_{u\in U}
|\langle Tu,u\rangle|,
\end{equation*}
\begin{equation*}
|\langle Tx_1,y_1\rangle|\leqslant \frac{1}{4} \sum_{u\in U}
|\langle Tu,u\rangle|,
\end{equation*} where ![]() $U=\left\{x_1+\eta y_1 \, : \, \eta= \pm 1, \pm i, \pm j, \pm k\right\}$. More precisely, for some
$U=\left\{x_1+\eta y_1 \, : \, \eta= \pm 1, \pm i, \pm j, \pm k\right\}$. More precisely, for some ![]() $u_0\in U$, we can write
$u_0\in U$, we can write
 \begin{eqnarray*}
|\langle Tx_1,y_1\rangle| & \leqslant & \frac{8}{4}
|\langle Tu_0,u_0 \rangle| = 2
\Bigg| \langle T\left(\frac{u_0}{\|u_0\|}\right), \frac{u_0}{\|u_0\|} \rangle\Bigg| \, \|u_0\|^2 \\
& \leqslant & 8
\Bigg| \langle T\left(\frac{u_0}{\|u_0\|}\right), \frac{u_0}{\|u_0\|} \rangle\Bigg|
\end{eqnarray*}
\begin{eqnarray*}
|\langle Tx_1,y_1\rangle| & \leqslant & \frac{8}{4}
|\langle Tu_0,u_0 \rangle| = 2
\Bigg| \langle T\left(\frac{u_0}{\|u_0\|}\right), \frac{u_0}{\|u_0\|} \rangle\Bigg| \, \|u_0\|^2 \\
& \leqslant & 8
\Bigg| \langle T\left(\frac{u_0}{\|u_0\|}\right), \frac{u_0}{\|u_0\|} \rangle\Bigg|
\end{eqnarray*} where in the last inequality we used the fact that ![]() $\|u_0\|\leqslant 2$. Set
$\|u_0\|\leqslant 2$. Set ![]() $\rho_1=u_0/ \|u_0\|\in {\mathcal{H}} $. Then, ρ 1 is a unit vector such that
$\rho_1=u_0/ \|u_0\|\in {\mathcal{H}} $. Then, ρ 1 is a unit vector such that
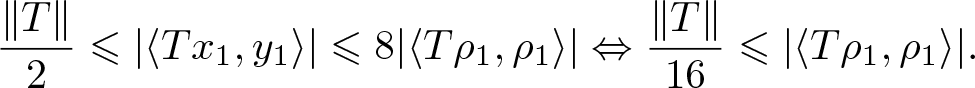 \begin{eqnarray*}
\frac{\lVert T\rVert}{2} \leqslant \lvert \langle Tx_1,y_1\rangle\rvert \leqslant 8 \lvert \langle T\rho_1, \rho_1\rangle \rvert
\Leftrightarrow
\frac{\lVert T\rVert}{16} \leqslant \lvert \langle T\rho_1, \rho_1\rangle \rvert.
\end{eqnarray*}
\begin{eqnarray*}
\frac{\lVert T\rVert}{2} \leqslant \lvert \langle Tx_1,y_1\rangle\rvert \leqslant 8 \lvert \langle T\rho_1, \rho_1\rangle \rvert
\Leftrightarrow
\frac{\lVert T\rVert}{16} \leqslant \lvert \langle T\rho_1, \rho_1\rangle \rvert.
\end{eqnarray*} Now, let P 1 be the orthogonal projection onto ![]() ${\text{span}\,}\{\rho_1\}$. By applying the above argument to the operator
${\text{span}\,}\{\rho_1\}$. By applying the above argument to the operator ![]() $(I-P_1)T(I-P_1)$, we can find a unit vector ρ 2 orthogonal to ρ 1 such that
$(I-P_1)T(I-P_1)$, we can find a unit vector ρ 2 orthogonal to ρ 1 such that
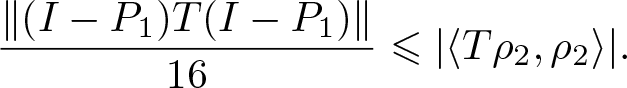 \begin{eqnarray*}
\frac{\lVert (I-P_1)T(I-P_1)\rVert}{16}
\leqslant \lvert \langle T\rho_2, \rho_2\rangle \rvert.
\end{eqnarray*}
\begin{eqnarray*}
\frac{\lVert (I-P_1)T(I-P_1)\rVert}{16}
\leqslant \lvert \langle T\rho_2, \rho_2\rangle \rvert.
\end{eqnarray*} Moreover, a recursive procedure allows us to construct an orthonormal sequence ![]() $(\rho_n)_{n}$ such that if Pn is the projection onto the span of
$(\rho_n)_{n}$ such that if Pn is the projection onto the span of ![]() $\{\rho_1, \dots, \rho_{n}\}$ then
$\{\rho_1, \dots, \rho_{n}\}$ then
 \begin{equation*}
\frac{\lVert (I-P_n)T(I-P_n) \rVert}{16} \leqslant \lvert \langle T\rho_{n+1}, \rho_{n+1}\rangle \rvert.
\end{equation*}
\begin{equation*}
\frac{\lVert (I-P_n)T(I-P_n) \rVert}{16} \leqslant \lvert \langle T\rho_{n+1}, \rho_{n+1}\rangle \rvert.
\end{equation*} Since ρn is an orthonormal sequence, by assumption, we have ![]() $\lim_{n\rightarrow \infty}\langle T\rho_n, \rho_n\rangle=0$, so that
$\lim_{n\rightarrow \infty}\langle T\rho_n, \rho_n\rangle=0$, so that
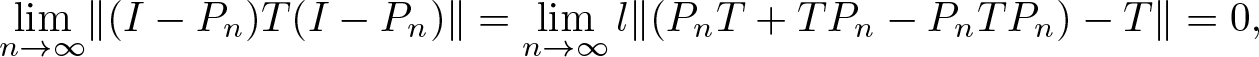 \begin{equation*}
\lim_{n\rightarrow \infty} \lVert (I-P_n)T(I-P_n) \rVert=\lim_{n\rightarrow \infty} l\Vert (P_nT+TP_n-P_nTP_n)-T\rVert=0,
\end{equation*}
\begin{equation*}
\lim_{n\rightarrow \infty} \lVert (I-P_n)T(I-P_n) \rVert=\lim_{n\rightarrow \infty} l\Vert (P_nT+TP_n-P_nTP_n)-T\rVert=0,
\end{equation*} and thus T is compact (being the limit of the finite rank operators ![]() $P_nT+TP_n-P_nTP_n$).
$P_nT+TP_n-P_nTP_n$).
Next result, well-known in the complex setting (see [Reference Filmore, Stampfli and Williams13, Corollary in page 189]), gives necessary and sufficient conditions for an element ![]() $q\in{\mathbb{H}}$ to belong to
$q\in{\mathbb{H}}$ to belong to ![]() $W_e(T)$, for some operator
$W_e(T)$, for some operator ![]() $T\in\mathcal{B}(\mathcal{H})$. A very important class of unitary vectors regarding the essential numerical range, portrayed below in condition (
$T\in\mathcal{B}(\mathcal{H})$. A very important class of unitary vectors regarding the essential numerical range, portrayed below in condition (![]() $b)$, will be called an essential sequence, see Definition 3.3. As usual, we write
$b)$, will be called an essential sequence, see Definition 3.3. As usual, we write ![]() $x_n\rightharpoonup x$ if a sequence
$x_n\rightharpoonup x$ if a sequence ![]() $(x_n)_n$ in
$(x_n)_n$ in ![]() $\mathcal{H}$ converges to
$\mathcal{H}$ converges to ![]() $x\in\mathcal{H}$ in the weak topology.
$x\in\mathcal{H}$ in the weak topology.
Theorem 3.2. Let ![]() $q\in {\mathbb{H}}$. The following conditions are equivalent:
$q\in {\mathbb{H}}$. The following conditions are equivalent:
(a)
 $q\in W_e(T)$.
$q\in W_e(T)$.(b) There exists a sequence of unit vectors
 $(x_n)_{n}$ in
$(x_n)_{n}$ in  ${\mathcal{H}}$ such that
${\mathcal{H}}$ such that  $x_n\rightharpoonup 0$ and
$x_n\rightharpoonup 0$ and  $\langle Tx_n,x_n\rangle\to q$.
$\langle Tx_n,x_n\rangle\to q$.(c) There exists an orthonormal sequence
 $(e_n)_{n}$ in
$(e_n)_{n}$ in  ${\mathcal{H}}$ such that
${\mathcal{H}}$ such that  $\langle Te_n,e_n\rangle\to q$.
$\langle Te_n,e_n\rangle\to q$.  $\lim_{n\rightarrow\infty}\langle T\xi_n,\xi_n\rangle=q$.
$\lim_{n\rightarrow\infty}\langle T\xi_n,\xi_n\rangle=q$.
Proof. ![]() $(b)\Rightarrow (a).\,$ Suppose (b) holds. To see that
$(b)\Rightarrow (a).\,$ Suppose (b) holds. To see that  $q\in \bigcap_{K\in{\mathcal{K}}({\mathcal{H}})}\overline{W(T+K)}$, we will show that
$q\in \bigcap_{K\in{\mathcal{K}}({\mathcal{H}})}\overline{W(T+K)}$, we will show that ![]() $\langle (T+K)x_n,x_n\rangle\to q$, for every compact operator K. At this point, we need the following well-known result: if K is compact and
$\langle (T+K)x_n,x_n\rangle\to q$, for every compact operator K. At this point, we need the following well-known result: if K is compact and ![]() $x_n\rightharpoonup x$, then
$x_n\rightharpoonup x$, then ![]() $Kx_n\to Kx$ strongly. In particular, if
$Kx_n\to Kx$ strongly. In particular, if ![]() $x_n\rightharpoonup 0$ then
$x_n\rightharpoonup 0$ then ![]() $\|Kx_n\|\to 0$. It follows that
$\|Kx_n\|\to 0$. It follows that
since we have ![]() $\left|\langle Kx_n,x_n\rangle\right|\leqslant\|Kx_n\|$, for every n.
$\left|\langle Kx_n,x_n\rangle\right|\leqslant\|Kx_n\|$, for every n.
![]() $(c)\Rightarrow (b).\,$ The result follows from the fact that
$(c)\Rightarrow (b).\,$ The result follows from the fact that ![]() $e_n\rightharpoonup 0$ for every orthonormal sequence
$e_n\rightharpoonup 0$ for every orthonormal sequence ![]() $(e_n)_n$.
$(e_n)_n$.
![]() $(a)\Rightarrow (c)$. Since
$(a)\Rightarrow (c)$. Since ![]() $W_e(T)=[B_e(T)]$, it is enough to prove the result for the essential upper bild. Let
$W_e(T)=[B_e(T)]$, it is enough to prove the result for the essential upper bild. Let ![]() $q\in B^+_e(T)$.
$q\in B^+_e(T)$.
From
![]() ${B_{e}^+(T)}\subseteq \overline{B^+(T)}$, there is a sequence of unit vectors
${B_{e}^+(T)}\subseteq \overline{B^+(T)}$, there is a sequence of unit vectors ![]() $(\xi_n)_n$ in
$(\xi_n)_n$ in ![]() ${\mathcal{H}}$ such that
${\mathcal{H}}$ such that ![]() $\langle T\xi_n,\xi_n\rangle\in B^+(T)$ and
$\langle T\xi_n,\xi_n\rangle\in B^+(T)$ and ![]() $\lim_{n\rightarrow\infty}\langle T\xi_n,\xi_n\rangle=q$.
$\lim_{n\rightarrow\infty}\langle T\xi_n,\xi_n\rangle=q$.
Take ξM, which we call without loss of generality ξ 1, such that
 \begin{equation*}
|\langle T\xi_1,\xi_1\rangle-q|\leqslant \frac{1}{2}.
\end{equation*}
\begin{equation*}
|\langle T\xi_1,\xi_1\rangle-q|\leqslant \frac{1}{2}.
\end{equation*} Let ![]() ${\mathcal{L}}_1:={\text{span}\,}\{\xi_1\}$ and write
${\mathcal{L}}_1:={\text{span}\,}\{\xi_1\}$ and write ![]() ${\mathcal{H}}={\mathcal{L}}_1\oplus{\mathcal{L}}_1^\bot$. Denote
${\mathcal{H}}={\mathcal{L}}_1\oplus{\mathcal{L}}_1^\bot$. Denote ![]() $P_1:{\mathcal{H}}\rightarrow{\mathcal{H}}$ the orthogonal projection onto
$P_1:{\mathcal{H}}\rightarrow{\mathcal{H}}$ the orthogonal projection onto ![]() ${\mathcal{L}}_1$. From [Reference Carvalho, Diogo and Mendes3, Corollary 3.3], we know that the quaternionic numerical range of an operator, and therefore its upper bild, always intersects the real line. So, we can take a real number
${\mathcal{L}}_1$. From [Reference Carvalho, Diogo and Mendes3, Corollary 3.3], we know that the quaternionic numerical range of an operator, and therefore its upper bild, always intersects the real line. So, we can take a real number  $\mu_1\in B^+\Big((I-P_1)\Big){T}|{{\mathcal{L}}_1^\bot}\Big)\cap{\mathbb{R}}$.
$\mu_1\in B^+\Big((I-P_1)\Big){T}|{{\mathcal{L}}_1^\bot}\Big)\cap{\mathbb{R}}$.
Let F 1 be the finite rank operator such that ![]() $ T+F_1 =\mu_1P_1+(I-P_1)T(I-P_1)$. Then, F 1 compact and, since
$ T+F_1 =\mu_1P_1+(I-P_1)T(I-P_1)$. Then, F 1 compact and, since ![]() $q\in B_e^+(T)$, it follows that
$q\in B_e^+(T)$, it follows that
However, it is clear that
 \begin{eqnarray*}
& &B^+\left(\mu_1P_1+(I-P_1)T(I-P_1)\right) =\\
&=& \left\{\langle (\mu_1P_1+(I-P_1)T(I-P_1)) (x_1+x_2), x_1+x_2 \rangle\, :\, (x_1,x_2)\in\Omega\right\} \cap {\mathbb{C}}^+ \\
&=& \left\{\mu_1\lVert x_1\rVert^2+\lVert x_2\rVert^2\langle (I-P_1)T \frac{x_2}{\|x_2\|},\frac{x_2}{\|x_2\|} \rangle\, :\, (x_1,x_2)\in\Omega\right\}\cap {\mathbb{C}}^+ ,
\end{eqnarray*}
\begin{eqnarray*}
& &B^+\left(\mu_1P_1+(I-P_1)T(I-P_1)\right) =\\
&=& \left\{\langle (\mu_1P_1+(I-P_1)T(I-P_1)) (x_1+x_2), x_1+x_2 \rangle\, :\, (x_1,x_2)\in\Omega\right\} \cap {\mathbb{C}}^+ \\
&=& \left\{\mu_1\lVert x_1\rVert^2+\lVert x_2\rVert^2\langle (I-P_1)T \frac{x_2}{\|x_2\|},\frac{x_2}{\|x_2\|} \rangle\, :\, (x_1,x_2)\in\Omega\right\}\cap {\mathbb{C}}^+ ,
\end{eqnarray*} where ![]() $\Omega=\left\{(x_1,x_2):x_1\in {\mathcal{L}}_1, x_2\in{\mathcal{L}}_1^\bot, \, \lVert x_1\rVert^2+\lVert x_2\rVert^2=1\right\}$.
$\Omega=\left\{(x_1,x_2):x_1\in {\mathcal{L}}_1, x_2\in{\mathcal{L}}_1^\bot, \, \lVert x_1\rVert^2+\lVert x_2\rVert^2=1\right\}$.
Since  $\mu_1\in B^+\Big((I-P_1)\Big){T}|{{\mathcal{L}}_1^\bot}\Big)\cap {\mathbb{R}}$ and
$\mu_1\in B^+\Big((I-P_1)\Big){T}|{{\mathcal{L}}_1^\bot}\Big)\cap {\mathbb{R}}$ and  $B^+\Big((I-P_1)\Big){T}|{{\mathcal{L}}_1^\bot}\Big)$ is convex (see [Reference Au-Yeung15, Corollary 1]), we obtain
$B^+\Big((I-P_1)\Big){T}|{{\mathcal{L}}_1^\bot}\Big)$ is convex (see [Reference Au-Yeung15, Corollary 1]), we obtain
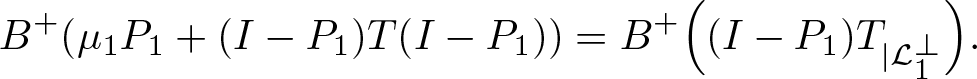 \begin{equation*}
B^+(\mu_1P_1+(I-P_1)T(I-P_1)) = B^+\Big((I-P_1)T_{|{\mathcal{L}}_1^\bot}\Big).
\end{equation*}
\begin{equation*}
B^+(\mu_1P_1+(I-P_1)T(I-P_1)) = B^+\Big((I-P_1)T_{|{\mathcal{L}}_1^\bot}\Big).
\end{equation*} Hence,  $q\in \overline{B^+\Big((I-P_1)\Big){T}|{{\mathcal{L}}_1^\bot}\Big)}$. So there is a unit vector
$q\in \overline{B^+\Big((I-P_1)\Big){T}|{{\mathcal{L}}_1^\bot}\Big)}$. So there is a unit vector ![]() $\xi_2\in {\mathcal{L}}_1^\bot$ such that
$\xi_2\in {\mathcal{L}}_1^\bot$ such that
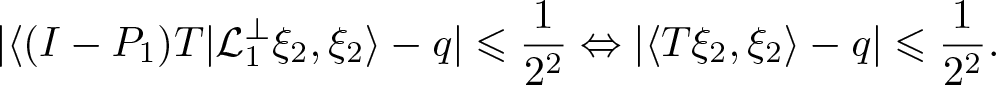 \begin{eqnarray*}
\lvert \langle (I-P_1){T}|{{\mathcal{L}}_1^\bot}\xi_2,\xi_2\rangle - q| \leqslant \frac{1}{2^2} & \Leftrightarrow & |\langle T \xi_2,\xi_2\rangle - q| \leqslant \frac{1}{2^2}.
\end{eqnarray*}
\begin{eqnarray*}
\lvert \langle (I-P_1){T}|{{\mathcal{L}}_1^\bot}\xi_2,\xi_2\rangle - q| \leqslant \frac{1}{2^2} & \Leftrightarrow & |\langle T \xi_2,\xi_2\rangle - q| \leqslant \frac{1}{2^2}.
\end{eqnarray*} If ![]() $\xi_1, \dots, \xi_n$ are orthonormal vectors such that
$\xi_1, \dots, \xi_n$ are orthonormal vectors such that  $|\langle T \xi_n,\xi_n\rangle - q| \leqslant \frac{1}{2^n},$ we can repeat the above procedure with
$|\langle T \xi_n,\xi_n\rangle - q| \leqslant \frac{1}{2^n},$ we can repeat the above procedure with ![]() ${\mathcal{L}}_n:={\text{span}\,}\{\xi_1, \dots, \xi_n\}$, Pn the orthogonal projection onto
${\mathcal{L}}_n:={\text{span}\,}\{\xi_1, \dots, \xi_n\}$, Pn the orthogonal projection onto ![]() ${\mathcal{L}}_n$,
${\mathcal{L}}_n$,  $\mu_n\in B^+\Big((I-P_n)\Big){T}|{{\mathcal{L}}_n^\bot}\Big)\cap{\mathbb{R}}$ and Fn such that
$\mu_n\in B^+\Big((I-P_n)\Big){T}|{{\mathcal{L}}_n^\bot}\Big)\cap{\mathbb{R}}$ and Fn such that ![]() $T+F_n=\mu_nP_n+(I-P_n)T(I-P_n)$. We thus obtain a unit vector
$T+F_n=\mu_nP_n+(I-P_n)T(I-P_n)$. We thus obtain a unit vector ![]() $\xi_{n+1}$ orthogonal to each ξk for
$\xi_{n+1}$ orthogonal to each ξk for ![]() $1\leqslant k\leqslant n$ such that
$1\leqslant k\leqslant n$ such that
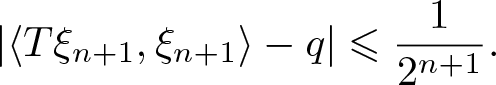 \begin{equation*}
|\langle T \xi_{n+1},\xi_{n+1}\rangle - q| \leqslant \frac{1}{2^{n+1}}.
\end{equation*}
\begin{equation*}
|\langle T \xi_{n+1},\xi_{n+1}\rangle - q| \leqslant \frac{1}{2^{n+1}}.
\end{equation*} By recursion, there exists an orthonormal sequence ![]() $(\xi_n)_{n}$ in
$(\xi_n)_{n}$ in ![]() ${\mathcal{H}}$ such that
${\mathcal{H}}$ such that ![]() $\langle T\xi_n,\xi_n\rangle\to q$.
$\langle T\xi_n,\xi_n\rangle\to q$.
We will call any sequence satisfying (b) an essential sequence for q, as stated in the following definition.
Definition 3.3. An essential sequence ![]() $(x_n)_{n}\subset {\mathcal{H}}$ for q is a sequence of unit vectors such that
$(x_n)_{n}\subset {\mathcal{H}}$ for q is a sequence of unit vectors such that ![]() $x_n\rightharpoonup 0$ and
$x_n\rightharpoonup 0$ and ![]() $\langle Tx_n,x_n\rangle\to q$.
$\langle Tx_n,x_n\rangle\to q$.
An immediate consequence of Theorem 3.2 is the non-emptiness of the essential numerical range. In fact, for any orthonormal sequence ![]() $(e_n)_{n}$, the sequence
$(e_n)_{n}$, the sequence  $\Big(\langle Te_n,e_n\rangle\Big)_{n}$ is bounded by
$\Big(\langle Te_n,e_n\rangle\Big)_{n}$ is bounded by ![]() $\|T\|$. Then, it has a convergent subsequence. By (c) in Theorem 3.2, we have that
$\|T\|$. Then, it has a convergent subsequence. By (c) in Theorem 3.2, we have that ![]() $W_e(T)$ is non-empty. Moreover, it is clear that
$W_e(T)$ is non-empty. Moreover, it is clear that ![]() $W_e(T)$ is a compact set since it is closed and bounded in
$W_e(T)$ is a compact set since it is closed and bounded in ![]() $\mathbb{H}$. These properties are summarized in the corollary below.
$\mathbb{H}$. These properties are summarized in the corollary below.
Corollary 3.4. ![]() $W_e(T)$ is a non-empty and compact set.
$W_e(T)$ is a non-empty and compact set.
The essential numerical range in the quaternionic setting shares many properties with either the complex essential numerical range or the quaternionic numerical range. We collect some of such properties below. The proofs are direct and for that reason only a short hint is provided.
Proposition 3.5. The following properties of the quaternionic essential numerical range hold.
(i)
 $W_e(T+K)=W_e(T)$, for all
$W_e(T+K)=W_e(T)$, for all  $K\in{\mathcal{K}}({\mathcal{H}})$.
$K\in{\mathcal{K}}({\mathcal{H}})$.(ii)
 $q\in W_e(T)$ if and only if
$q\in W_e(T)$ if and only if  $[q]\subseteq W_e(T)$.
$[q]\subseteq W_e(T)$.(iii)
 $W_e(T^*)=W_e(T)$.
$W_e(T^*)=W_e(T)$.(iv)
 $W_e(T)\subseteq \overline{{\mathbb{D}}(0, \|\pi(T)\|)}$.
$W_e(T)\subseteq \overline{{\mathbb{D}}(0, \|\pi(T)\|)}$.(v) If
 $a,b\in{\mathbb{R}}, W_e(aT+bI)=aW_e(T)+b$.
$a,b\in{\mathbb{R}}, W_e(aT+bI)=aW_e(T)+b$.(vi)
 $W_e(T+S)\subseteq W_e(T)+W_e(S)$.
$W_e(T+S)\subseteq W_e(T)+W_e(S)$.(vii) If
 $U\in{\mathcal{B}}({\mathcal{H}})$ is unitary, then
$U\in{\mathcal{B}}({\mathcal{H}})$ is unitary, then  $W_e(UTU^*)=W_e(T)$.
$W_e(UTU^*)=W_e(T)$.(viii)
 $W_e(T)$ contains all eigenvalues of T of infinite multiplicity.
$W_e(T)$ contains all eigenvalues of T of infinite multiplicity.
Proof. (i) follows from ![]() $K+{\mathcal{K}}({\mathcal{H}})={\mathcal{K}}({\mathcal{H}}) $, for any
$K+{\mathcal{K}}({\mathcal{H}})={\mathcal{K}}({\mathcal{H}}) $, for any ![]() $K \in{\mathcal{K}}({\mathcal{H}})$; (ii) results from
$K \in{\mathcal{K}}({\mathcal{H}})$; (ii) results from ![]() $q\in {W(T)}$ if and only if
$q\in {W(T)}$ if and only if ![]() $[q]\subseteq {W(T)}$, for every operator T; (iii) is a consequence of
$[q]\subseteq {W(T)}$, for every operator T; (iii) is a consequence of ![]() $W(T^*)=W(T)$, for every
$W(T^*)=W(T)$, for every ![]() $T \in {\mathcal{B}}({\mathcal{H}})$; the inclusion
$T \in {\mathcal{B}}({\mathcal{H}})$; the inclusion ![]() $W(T)\subseteq \overline{{\mathbb{D}}(0, \|T\|)}$ implies (iv); (v) holds because
$W(T)\subseteq \overline{{\mathbb{D}}(0, \|T\|)}$ implies (iv); (v) holds because ![]() $W(aT+bI)=aW(T)+b$, for
$W(aT+bI)=aW(T)+b$, for ![]() $a,b\in{\mathbb{R}}$; from
$a,b\in{\mathbb{R}}$; from ![]() ${\mathcal{K}}({\mathcal{H}})+{\mathcal{K}}({\mathcal{H}})={\mathcal{K}}({\mathcal{H}})$ and
${\mathcal{K}}({\mathcal{H}})+{\mathcal{K}}({\mathcal{H}})={\mathcal{K}}({\mathcal{H}})$ and ![]() $W(T+S)\subseteq W(T)+W(S)$ we obtain (vi); (vii) follows from
$W(T+S)\subseteq W(T)+W(S)$ we obtain (vi); (vii) follows from ![]() $W(UTU^*)=W(T)$; for (viii) note that the orthonormal set
$W(UTU^*)=W(T)$; for (viii) note that the orthonormal set ![]() $(e_n)_{n}$ of eigenvectors satisfying
$(e_n)_{n}$ of eigenvectors satisfying ![]() $Te_n=e_n q$ is an essential sequence for q.
$Te_n=e_n q$ is an essential sequence for q.
From [Reference Carvalho, Diogo and Mendes6, Theorem 2.9], we know that ![]() $\sigma^S(T+K) \subseteq \overline{W(T+K)}$, for every
$\sigma^S(T+K) \subseteq \overline{W(T+K)}$, for every ![]() $K\in {\mathcal{K}}({\mathcal{H}})$. Using the notion of Weyl S-spectrum,
$K\in {\mathcal{K}}({\mathcal{H}})$. Using the notion of Weyl S-spectrum,  $\sigma_w^S(T):= \bigcap_{K\in {\mathcal{K}}({\mathcal{H}})}\sigma^S(T+K) $, and that
$\sigma_w^S(T):= \bigcap_{K\in {\mathcal{K}}({\mathcal{H}})}\sigma^S(T+K) $, and that ![]() $\sigma_{e}^S(T)\subseteq \sigma_w^S(T)\subseteq \sigma^S(T)$ (see Definition 6.1 and Theorem 6.6 in [Reference Muraleetharan and Kengathram12]), we have the following result.
$\sigma_{e}^S(T)\subseteq \sigma_w^S(T)\subseteq \sigma^S(T)$ (see Definition 6.1 and Theorem 6.6 in [Reference Muraleetharan and Kengathram12]), we have the following result.
Theorem 3.6. ![]() $\sigma_e^S(T)\subseteq W_e(T)$.
$\sigma_e^S(T)\subseteq W_e(T)$.
4. Convexity
In this section, we establish the main result of the paper which asserts that the quaternionic essential numerical range is convex. To see this, we will show that for any two elements ![]() ${\omega^{(1)}}, {\omega^{(2)}}$ in
${\omega^{(1)}}, {\omega^{(2)}}$ in ![]() $W_e(T)$, their convex combination can be arbitrarily approximated by elements
$W_e(T)$, their convex combination can be arbitrarily approximated by elements ![]() $\langle Tz, z\rangle$, where
$\langle Tz, z\rangle$, where ![]() $z \in {\mathcal{H}}$ is generated by an essential sequence for
$z \in {\mathcal{H}}$ is generated by an essential sequence for ![]() ${\omega^{(1)}}$ and an essential sequence for
${\omega^{(1)}}$ and an essential sequence for ![]() ${\omega^{(2)}}$. To construct such elements
${\omega^{(2)}}$. To construct such elements ![]() $z\in{\mathcal{H}}$, we need a preparatory lemma which states a general property enjoyed by a pair of unitary sequences weakly vanishing and a bounded linear operator.
$z\in{\mathcal{H}}$, we need a preparatory lemma which states a general property enjoyed by a pair of unitary sequences weakly vanishing and a bounded linear operator.
Lemma 4.1. Let ![]() $T\in B({\mathcal{H}})$ and
$T\in B({\mathcal{H}})$ and  $\big(x^{(i)}_n\big)_n$,
$\big(x^{(i)}_n\big)_n$, ![]() $i=1,2$, be unitary sequences in
$i=1,2$, be unitary sequences in ![]() ${\mathcal{H}}$ such that
${\mathcal{H}}$ such that ![]() $x_n^{(i)}\rightharpoonup 0$. For any ɛ > 0 and
$x_n^{(i)}\rightharpoonup 0$. For any ɛ > 0 and ![]() $N \in {\mathbb{N}}$, there is
$N \in {\mathbb{N}}$, there is ![]() $M \in {\mathbb{N}}$ such that
$M \in {\mathbb{N}}$ such that ![]() $M\geqslant N $ and
$M\geqslant N $ and
 \begin{equation*}
\big|\langle{x^{(1)}_N}{x^{(2)}_M}\rangle\big|\leqslant {\varepsilon}, \quad \big|\langle{Tx^{(1)}_N}{x^{(2)}_M}\rangle\big|\leqslant {\varepsilon} \quad\text{and} \quad \big|\langle{T^*x^{(1)}_N}{x^{(2)}_M}\rangle\big|\leqslant {\varepsilon}.
\end{equation*}
\begin{equation*}
\big|\langle{x^{(1)}_N}{x^{(2)}_M}\rangle\big|\leqslant {\varepsilon}, \quad \big|\langle{Tx^{(1)}_N}{x^{(2)}_M}\rangle\big|\leqslant {\varepsilon} \quad\text{and} \quad \big|\langle{T^*x^{(1)}_N}{x^{(2)}_M}\rangle\big|\leqslant {\varepsilon}.
\end{equation*}Proof. Let ![]() $\delta \gt 0$. Let
$\delta \gt 0$. Let ![]() $(e_{k})_{k}$ be an orthonormal basis for
$(e_{k})_{k}$ be an orthonormal basis for ![]() ${\mathcal{H}}$ and
${\mathcal{H}}$ and ![]() $P_{K}$ be the projection onto
span
$P_{K}$ be the projection onto
span ![]() $\{ e_{1} ,..., e_{k} \}$. Since
$\{ e_{1} ,..., e_{k} \}$. Since  $(I - P_{K})_{y} {\longrightarrow \atop {k \rightarrow \infty}} 0 $ for every
$(I - P_{K})_{y} {\longrightarrow \atop {k \rightarrow \infty}} 0 $ for every ![]() $y \in \mathcal{H}$, then, for the above
$y \in \mathcal{H}$, then, for the above ![]() $\delta \gt 0$ and
$\delta \gt 0$ and
![]() $N \in {\mathbb{N}}$, we may find
$N \in {\mathbb{N}}$, we may find ![]() $K \in {\mathbb{N}}$ such that
$K \in {\mathbb{N}}$ such that
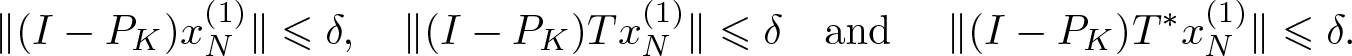 \begin{equation}
\|(I-P_K)x^{(1)}_N\|\leqslant \delta, \quad \|(I-P_K)Tx^{(1)}_N\|\leqslant \delta \quad\text{and }\quad \|(I-P_K)T^* x^{(1)}_N\|\leqslant \delta.
\end{equation}
\begin{equation}
\|(I-P_K)x^{(1)}_N\|\leqslant \delta, \quad \|(I-P_K)Tx^{(1)}_N\|\leqslant \delta \quad\text{and }\quad \|(I-P_K)T^* x^{(1)}_N\|\leqslant \delta.
\end{equation} We can find an ![]() $M\in\mathbb{N}$ that depends on δ, N, K, such that
$M\in\mathbb{N}$ that depends on δ, N, K, such that ![]() $M \geqslant N$ and
$M \geqslant N$ and
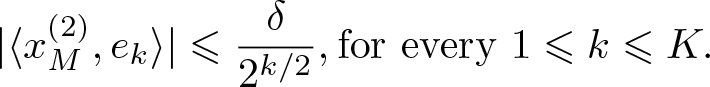 \begin{equation}
|\langle x^{(2)}_M, e_k\rangle | \leqslant \frac{\delta}{2^{k/2}}, \text{for every } 1 \leqslant k \leqslant K.
\end{equation}
\begin{equation}
|\langle x^{(2)}_M, e_k\rangle | \leqslant \frac{\delta}{2^{k/2}}, \text{for every } 1 \leqslant k \leqslant K.
\end{equation} Inequality (4.2) follows from the fact that  $\big(x^{(2)}_n\big)_n$ vanishes weakly and that implies coordinatewise convergence to zero. It follows that
$\big(x^{(2)}_n\big)_n$ vanishes weakly and that implies coordinatewise convergence to zero. It follows that
 \begin{equation*}
\Big\|\sum_{1\leqslant k \leqslant K} \langle x^{(2)}_M, e_k\rangle \;e_k\Big\|^2 = \sum_{1\leqslant k \leqslant K} \Big| \langle x^{(2)}_M, e_k\rangle \Big|^2 \leqslant \delta^2
\end{equation*}
\begin{equation*}
\Big\|\sum_{1\leqslant k \leqslant K} \langle x^{(2)}_M, e_k\rangle \;e_k\Big\|^2 = \sum_{1\leqslant k \leqslant K} \Big| \langle x^{(2)}_M, e_k\rangle \Big|^2 \leqslant \delta^2
\end{equation*}and therefore
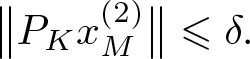 \begin{equation}
\big\|P_K x^{(2)}_M\big\|\leqslant \delta.
\end{equation}
\begin{equation}
\big\|P_K x^{(2)}_M\big\|\leqslant \delta.
\end{equation} Noting that  $\Vert x^{(1)}_N\rVert=\lVert x^{(2)}_M\rVert=1$, we have
$\Vert x^{(1)}_N\rVert=\lVert x^{(2)}_M\rVert=1$, we have
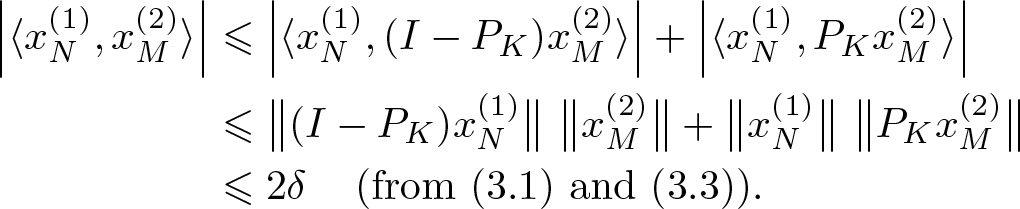 \begin{align*}
\Big|\langle x^{(1)}_N, x^{(2)}_M\rangle\Big| &\leqslant \Big| \langle x^{(1)}_N, (I-P_K)x^{(2)}_M\rangle \Big| + \Big| \langle x^{(1)}_N, P_K x^{(2)}_M\rangle \Big| \\
&\leqslant\big\| (I-P_K)x^{(1)}_N\big\| \,\,\big\| x^{(2)}_M \big\| + \big\| x^{(1)}_N\big\|\,\,\big\|P_K x^{(2)}_M\big\|\\
&\leqslant 2\delta \,\,\,\,\,\,\,(\textrm{from}\,\,(3.1)\,\,\text{and}\,\,({3.3})).
\end{align*}
\begin{align*}
\Big|\langle x^{(1)}_N, x^{(2)}_M\rangle\Big| &\leqslant \Big| \langle x^{(1)}_N, (I-P_K)x^{(2)}_M\rangle \Big| + \Big| \langle x^{(1)}_N, P_K x^{(2)}_M\rangle \Big| \\
&\leqslant\big\| (I-P_K)x^{(1)}_N\big\| \,\,\big\| x^{(2)}_M \big\| + \big\| x^{(1)}_N\big\|\,\,\big\|P_K x^{(2)}_M\big\|\\
&\leqslant 2\delta \,\,\,\,\,\,\,(\textrm{from}\,\,(3.1)\,\,\text{and}\,\,({3.3})).
\end{align*}Using a similar reasoning, we can show that
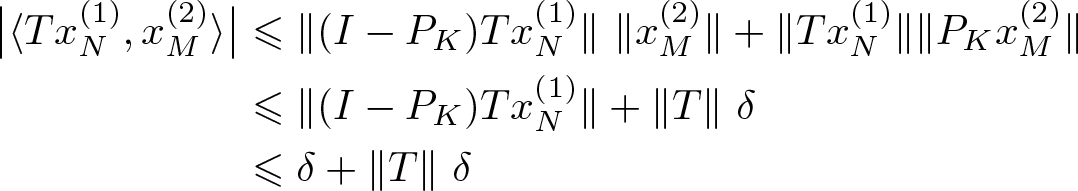 \begin{align*}
\big|\langle Tx^{(1)}_N, x^{(2)}_M\rangle\big|&\leqslant \| (I-P_K)Tx^{(1)}_N\|\,\, \|x^{(2)}_M\|+\|Tx^{(1)}_N\| \| P_K x^{(2)}_M\|\\
&\leqslant \| (I-P_K)Tx^{(1)}_N\|+\|T\| \,\, \delta \\
&\leqslant \delta+\|T\| \,\, \delta
\end{align*}
\begin{align*}
\big|\langle Tx^{(1)}_N, x^{(2)}_M\rangle\big|&\leqslant \| (I-P_K)Tx^{(1)}_N\|\,\, \|x^{(2)}_M\|+\|Tx^{(1)}_N\| \| P_K x^{(2)}_M\|\\
&\leqslant \| (I-P_K)Tx^{(1)}_N\|+\|T\| \,\, \delta \\
&\leqslant \delta+\|T\| \,\, \delta
\end{align*} and  $\big|\langle T^*x^{(1)}_N, x^{(2)}_M\rangle\big|\leqslant \delta+\|T\| \,\, \delta$. Letting δ be such that
$\big|\langle T^*x^{(1)}_N, x^{(2)}_M\rangle\big|\leqslant \delta+\|T\| \,\, \delta$. Letting δ be such that ![]() $\max\{2, 1+\|T\|\}\delta\leqslant {\varepsilon}$ the lemma follows.
$\max\{2, 1+\|T\|\}\delta\leqslant {\varepsilon}$ the lemma follows.
Theorem 4.2. ![]() $ W_e(T)$ is convex.
$ W_e(T)$ is convex.
Proof. Convexity of ![]() $W_e(T)$ will be proved by showing that
$W_e(T)$ will be proved by showing that ![]() $\alpha^2{\omega^{(1)}}+\beta^2{\omega^{(2)}} \in W_e(T)$ for any
$\alpha^2{\omega^{(1)}}+\beta^2{\omega^{(2)}} \in W_e(T)$ for any ![]() $\alpha^2+\beta^2=1$, when
$\alpha^2+\beta^2=1$, when ![]() ${\omega^{(1)}}, {\omega^{(2)}}$ lie in
${\omega^{(1)}}, {\omega^{(2)}}$ lie in ![]() $W_e(T)$. For that we will prove there is an essential sequence
$W_e(T)$. For that we will prove there is an essential sequence ![]() $(\tilde z_p)_p$ for
$(\tilde z_p)_p$ for ![]() $\alpha^2{\omega^{(1)}}+\beta^2{\omega^{(2)}}$.
$\alpha^2{\omega^{(1)}}+\beta^2{\omega^{(2)}}$.
Let  $\big(x^{(i)}_n\big)_n$ be an essential sequence for
$\big(x^{(i)}_n\big)_n$ be an essential sequence for ![]() $\omega^{(i)}$ and denote
$\omega^{(i)}$ and denote  $\omega_n^{(i)}=\langle Tx^{(i)}_n, x^{(i)}_n\rangle$, for
$\omega_n^{(i)}=\langle Tx^{(i)}_n, x^{(i)}_n\rangle$, for ![]() $i=1,2$. For any
$i=1,2$. For any ![]() $p\in {\mathbb{N}}$ let
$p\in {\mathbb{N}}$ let ![]() ${\varepsilon}=1/p$. One of the conditions for the sequence
${\varepsilon}=1/p$. One of the conditions for the sequence  $\big(x^{(i)}_n\big)_n$ to be essential for
$\big(x^{(i)}_n\big)_n$ to be essential for ![]() $\omega{i}$ is that
$\omega{i}$ is that ![]() $\omega{i}_n \to \omega{i}$ when
$\omega{i}_n \to \omega{i}$ when ![]() $n \to \infty$. Hence, for the given ɛ, there exists
$n \to \infty$. Hence, for the given ɛ, there exists ![]() $N\geqslant p$ satisfying
$N\geqslant p$ satisfying
Pick M according to the previous lemma. For the fixed α and β, let  $z=\alpha x^{(1)}_N+\beta x^{(2)}_M$. Since
$z=\alpha x^{(1)}_N+\beta x^{(2)}_M$. Since ![]() $\alpha^2+\beta^2=1$ and
$\alpha^2+\beta^2=1$ and  $\alpha \beta \leqslant \frac{1}{2}$, we easily verify that
$\alpha \beta \leqslant \frac{1}{2}$, we easily verify that
 \begin{equation}\\
\big|\|z\|^2-1\big|\leqslant \big|\langle x^{(1)}_N, x^{(2)}_M\rangle \big|\leqslant {\varepsilon}.
\end{equation}
\begin{equation}\\
\big|\|z\|^2-1\big|\leqslant \big|\langle x^{(1)}_N, x^{(2)}_M\rangle \big|\leqslant {\varepsilon}.
\end{equation}A simple computation shows that
 \begin{align*}
\Big|\langle T z, z\rangle - \big(\alpha^2{\omega^{(1)}}_N+\beta^2{\omega^{(2)}}_M\big)\Big| &= \alpha\beta\Big|\langle Tx^{(1)}_N, x^{(2)}_M\rangle + \overline{\langle T^*x^{(1)}_N, x^{(2)}_M\rangle} \Big| \leqslant {\varepsilon}.\nonumber
\end{align*}
\begin{align*}
\Big|\langle T z, z\rangle - \big(\alpha^2{\omega^{(1)}}_N+\beta^2{\omega^{(2)}}_M\big)\Big| &= \alpha\beta\Big|\langle Tx^{(1)}_N, x^{(2)}_M\rangle + \overline{\langle T^*x^{(1)}_N, x^{(2)}_M\rangle} \Big| \leqslant {\varepsilon}.\nonumber
\end{align*}From (4.4), it follows that
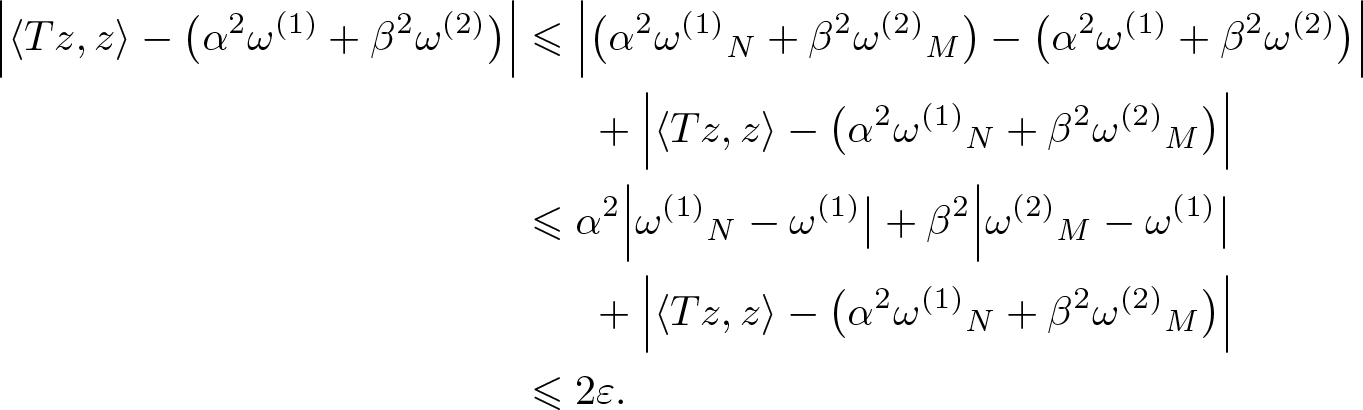 \begin{align}
\Big|\langle T z, z\rangle - \big(\alpha^2{\omega^{(1)}}+\beta^2{\omega^{(2)}}\big)\Big|&\leqslant \Big| \big(\alpha^2{\omega^{(1)}}_N+\beta^2{\omega^{(2)}}_M\big)-\big(\alpha^2{\omega^{(1)}}+\beta^2{\omega^{(2)}}\big) \Big|\nonumber\\
& \,\,\,\,\,\,\,\,\,\,+ \Big|\langle T z, z\rangle - \big(\alpha^2{\omega^{(1)}}_N+\beta^2{\omega^{(2)}}_M\big)\Big|\nonumber\\
&\leqslant \alpha^2 \Big|{\omega^{(1)}}_N - {\omega^{(1)}}\big|+ \beta^2 \Big|{\omega^{(2)}}_M - {\omega^{(1)}}\big|\nonumber\\
& \,\,\,\,\,\,\,\,\,\,+\Big|\langle T z, z\rangle - \big(\alpha^2{\omega^{(1)}}_N+\beta^2{\omega^{(2)}}_M\big)\Big| \nonumber\\
&\leqslant 2{\varepsilon}.
\end{align}
\begin{align}
\Big|\langle T z, z\rangle - \big(\alpha^2{\omega^{(1)}}+\beta^2{\omega^{(2)}}\big)\Big|&\leqslant \Big| \big(\alpha^2{\omega^{(1)}}_N+\beta^2{\omega^{(2)}}_M\big)-\big(\alpha^2{\omega^{(1)}}+\beta^2{\omega^{(2)}}\big) \Big|\nonumber\\
& \,\,\,\,\,\,\,\,\,\,+ \Big|\langle T z, z\rangle - \big(\alpha^2{\omega^{(1)}}_N+\beta^2{\omega^{(2)}}_M\big)\Big|\nonumber\\
&\leqslant \alpha^2 \Big|{\omega^{(1)}}_N - {\omega^{(1)}}\big|+ \beta^2 \Big|{\omega^{(2)}}_M - {\omega^{(1)}}\big|\nonumber\\
& \,\,\,\,\,\,\,\,\,\,+\Big|\langle T z, z\rangle - \big(\alpha^2{\omega^{(1)}}_N+\beta^2{\omega^{(2)}}_M\big)\Big| \nonumber\\
&\leqslant 2{\varepsilon}.
\end{align} Observing that the fixed integers N and M depend on ɛ, that is on ![]() $p\in{\mathbb{N}}$, we denote them by Np and Mp; likewise, we denote z by zp. To get an essential sequence, we have to normalize
$p\in{\mathbb{N}}$, we denote them by Np and Mp; likewise, we denote z by zp. To get an essential sequence, we have to normalize ![]() $(z_p)_p$. Write
$(z_p)_p$. Write  $\tilde z_p=\frac{z_p}{\|z_p\|}$. From (4.5),
$\tilde z_p=\frac{z_p}{\|z_p\|}$. From (4.5), ![]() $\|z_p\|\to 1\,\,(p\to\infty)$, and so
$\|z_p\|\to 1\,\,(p\to\infty)$, and so ![]() $(\tilde z_p)_p$ is well defined. By definition,
$(\tilde z_p)_p$ is well defined. By definition,  $z_p=\alpha x^{(1)}_{N_p}+\beta x^{(2)}_{M_p}$, and
$z_p=\alpha x^{(1)}_{N_p}+\beta x^{(2)}_{M_p}$, and  $x^{(1)}_{N_p}, x^{(2)}_{M_p} \rightharpoonup 0$, when
$x^{(1)}_{N_p}, x^{(2)}_{M_p} \rightharpoonup 0$, when ![]() $p \to \infty$. By linearity and since
$p \to \infty$. By linearity and since ![]() $\|z_p\|\to 1$, we have that
$\|z_p\|\to 1$, we have that ![]() $\tilde z_p \rightharpoonup 0$. Finally, from (4.6) it follows that
$\tilde z_p \rightharpoonup 0$. Finally, from (4.6) it follows that
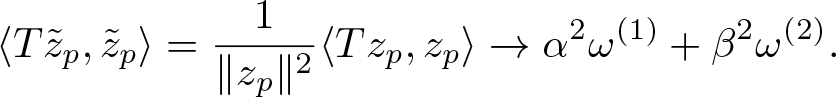 \begin{equation*}
\langle T \tilde z_p, \tilde z_p\rangle = \frac{1}{\|z_p\|^2} \langle T z_p, z_p\rangle \to \alpha^2{\omega^{(1)}}+\beta^2{\omega^{(2)}}.
\end{equation*}
\begin{equation*}
\langle T \tilde z_p, \tilde z_p\rangle = \frac{1}{\|z_p\|^2} \langle T z_p, z_p\rangle \to \alpha^2{\omega^{(1)}}+\beta^2{\omega^{(2)}}.
\end{equation*} The sequence ![]() $(\tilde z_p)_p$ is essential for
$(\tilde z_p)_p$ is essential for ![]() $\alpha^2{\omega^{(1)}}+\beta^2{\omega^{(2)}}$ and thus, by Theorem 3.2,
$\alpha^2{\omega^{(1)}}+\beta^2{\omega^{(2)}}$ and thus, by Theorem 3.2, ![]() $\alpha^2{\omega^{(1)}}+\beta^2{\omega^{(2)}}\in W_e(T).$
$\alpha^2{\omega^{(1)}}+\beta^2{\omega^{(2)}}\in W_e(T).$
Next result establishes the relation between the boundary of the numerical range and the essential numerical range. This is the quaternionic analogue of Lancaster’s theorem for the complex numerical range, see [Reference Lancaster11, Theorem 1]. Since the quaternionic numerical range is not always convex, a modification is imposed and we need to introduce the notion of inter-convex hull of sets (see [Reference Carvalho, Diogo and Mendes2, Definition 3.2]).
The inter-convex hull of the sets A and B, denoted by ![]() ${{\rm iconv\,}}\{A, B\}$, closes the set
${{\rm iconv\,}}\{A, B\}$, closes the set ![]() $A \cup B$ to the convex combinations with one element of each sets,
$A \cup B$ to the convex combinations with one element of each sets,
Theorem 4.3. The closure of the numerical range is ![]() $\overline{W(T)}={{\rm iconv\,}}\{W_e(T), W(T)\}$.
$\overline{W(T)}={{\rm iconv\,}}\{W_e(T), W(T)\}$.
Proof. We start proving that ![]() ${{\rm iconv\,}}\{W_e(T), W(T)\} \subseteq\overline{W(T)}$. Let
${{\rm iconv\,}}\{W_e(T), W(T)\} \subseteq\overline{W(T)}$. Let ![]() $\bar \omega \in {{\rm iconv\,}}\{W_e(T), W(T)\}$. Then
$\bar \omega \in {{\rm iconv\,}}\{W_e(T), W(T)\}$. Then ![]() $\bar{\omega}= \alpha^2 \omega+\beta^2 \omega_e$ with
$\bar{\omega}= \alpha^2 \omega+\beta^2 \omega_e$ with ![]() $\omega \in W(T), \omega_e \in W_e(T)$ and
$\omega \in W(T), \omega_e \in W_e(T)$ and ![]() $\alpha^2+\beta^2=1$. In particular, we can take a unitary
$\alpha^2+\beta^2=1$. In particular, we can take a unitary ![]() $y \in {\mathcal{H}}$ such that
$y \in {\mathcal{H}}$ such that ![]() $\omega=\langle{Ty},{y}\rangle$ and an essential sequence
$\omega=\langle{Ty},{y}\rangle$ and an essential sequence ![]() $(y_n)_n$ for ωe. Since
$(y_n)_n$ for ωe. Since ![]() $y_n \rightharpoonup 0$, we have that
$y_n \rightharpoonup 0$, we have that ![]() $\lim \,\langle T{y_n},{y}\rangle=\lim \, \langle T{y_n},{Ty}\rangle=\lim\,\langle T{y_n},{T^*y}\rangle=0$. Let
$\lim \,\langle T{y_n},{y}\rangle=\lim \, \langle T{y_n},{Ty}\rangle=\lim\,\langle T{y_n},{T^*y}\rangle=0$. Let ![]() $z_n=\alpha y+\beta y_n$. Then,
$z_n=\alpha y+\beta y_n$. Then,
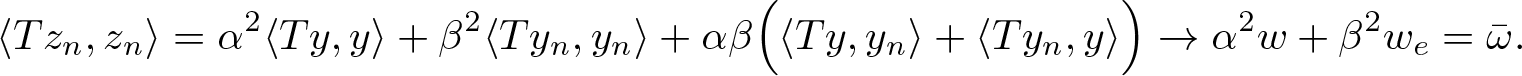 \begin{equation*}
\langle T{z_n},{z_n}\rangle=\alpha^2 \langle T{y,y}\rangle+\beta^2\langle T{y_n},y_n\rangle +\alpha\beta
\Big(\langle Ty,{y_n}\rangle+\langle{Ty_n},{y}\rangle\Big)
\to \alpha^2 w+\beta^2w_e=\bar{\omega}.
\end{equation*}
\begin{equation*}
\langle T{z_n},{z_n}\rangle=\alpha^2 \langle T{y,y}\rangle+\beta^2\langle T{y_n},y_n\rangle +\alpha\beta
\Big(\langle Ty,{y_n}\rangle+\langle{Ty_n},{y}\rangle\Big)
\to \alpha^2 w+\beta^2w_e=\bar{\omega}.
\end{equation*}Furthermore,
 \begin{equation*}\|z_n\|^2=\alpha^2\|y\|^2 +\beta^2\|y_n\|^2 +\alpha\beta\Big(\langle {y},{y_n}\rangle +\langle{y_n},{y}\rangle\Big)\to 1.
\end{equation*}
\begin{equation*}\|z_n\|^2=\alpha^2\|y\|^2 +\beta^2\|y_n\|^2 +\alpha\beta\Big(\langle {y},{y_n}\rangle +\langle{y_n},{y}\rangle\Big)\to 1.
\end{equation*} Thus,  $W(T) \ni \langle T{\frac{z_n}{\|z_n\|}},{\frac{z_n}{\|z_n\|}}\rangle \to \bar\omega$ and
$W(T) \ni \langle T{\frac{z_n}{\|z_n\|}},{\frac{z_n}{\|z_n\|}}\rangle \to \bar\omega$ and ![]() $\bar\omega \in \overline{W(T)}$.
$\bar\omega \in \overline{W(T)}$.
To prove the converse inclusion, take ![]() $\overline\omega \in \overline{W(T)}$. There is a sequence
$\overline\omega \in \overline{W(T)}$. There is a sequence ![]() $\left(y_n\right)_n$ in
$\left(y_n\right)_n$ in ![]() ${\mathcal{H}}$ satisfying
${\mathcal{H}}$ satisfying ![]() $\|y_n\|=1$ and
$\|y_n\|=1$ and ![]() $\omega_n=\langle T y_n, y_n\rangle \to \overline\omega $. Since this sequence is in the unit circle, there is an element
$\omega_n=\langle T y_n, y_n\rangle \to \overline\omega $. Since this sequence is in the unit circle, there is an element ![]() $y \in {\mathcal{H}}$ in the unit disk such that yn converges weakly to y.
$y \in {\mathcal{H}}$ in the unit disk such that yn converges weakly to y.
If y = 0, then ![]() $(y_n)_n$ is an essential sequence for
$(y_n)_n$ is an essential sequence for ![]() $\overline\omega$. From Theorem 3.2, we have
$\overline\omega$. From Theorem 3.2, we have ![]() $\overline\omega \in W_e(T)$.
$\overline\omega \in W_e(T)$.
If ![]() $\|y\|=1$, we have that
$\|y\|=1$, we have that ![]() $y_n\rightharpoonup y$, with
$y_n\rightharpoonup y$, with ![]() $\|y\|=1=\|y_n\|$. It is well-known that in this case
$\|y\|=1=\|y_n\|$. It is well-known that in this case ![]() $y_n \rightarrow y$ (strongly). Thus,
$y_n \rightarrow y$ (strongly). Thus, ![]() $\langle T{y_n}, y_n\rangle \to \langle Ty,y \rangle$, that is,
$\langle T{y_n}, y_n\rangle \to \langle Ty,y \rangle$, that is, ![]() $ \overline\omega = \langle Ty , y \rangle\in W(T)$.
$ \overline\omega = \langle Ty , y \rangle\in W(T)$.
Assume now that ![]() $\|y\| \neq 0,1$. Using that
$\|y\| \neq 0,1$. Using that ![]() $\langle y_n, h\rangle \to \langle y, h\rangle$ for any
$\langle y_n, h\rangle \to \langle y, h\rangle$ for any ![]() $ h \in {\mathcal{H}}$, we can prove that
$ h \in {\mathcal{H}}$, we can prove that ![]() $\lim \;\langle Ty_n, y\rangle=\lim \;\langle Ty, y_n\rangle= \langle Ty, y\rangle$ and therefore
$\lim \;\langle Ty_n, y\rangle=\lim \;\langle Ty, y_n\rangle= \langle Ty, y\rangle$ and therefore
It is easy to see that ![]() $\lim \|y_n-y\|^2= 1-\|y\|^2$. Then
$\lim \|y_n-y\|^2= 1-\|y\|^2$. Then
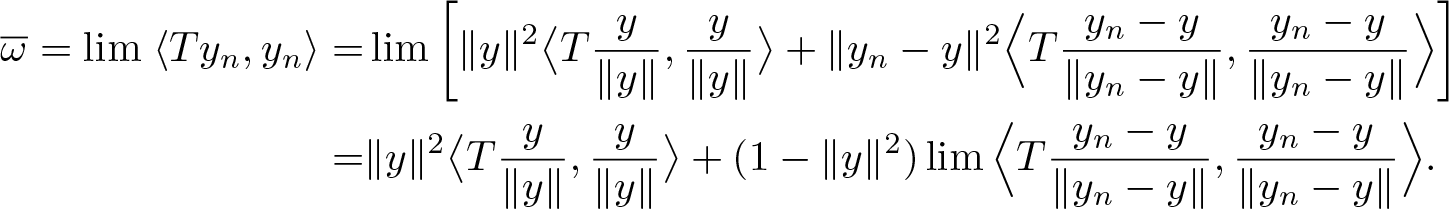 \begin{align*}
\overline\omega=\lim\;\langle Ty_n, y_n\rangle= & \lim \left[\|y\|^2 \big\langle T\frac{y}{\|y\|}, \frac{y}{\|y\|}\big\rangle + \|y_n-y\|^2\Big\langle T\frac{y_n-y}{\|y_n-y\|}, \frac{y_n-y}{\|y_n-y\|}\Big\rangle\right]\\
=& \|y\|^2 \big\langle T\frac{y}{\|y\|}, \frac{y}{\|y\|}\big\rangle + (1-\|y\|^2)\lim \Big\langle T\frac{y_n-y}{\|y_n-y\|}, \frac{y_n-y}{\|y_n-y\|}\Big\rangle .
\end{align*}
\begin{align*}
\overline\omega=\lim\;\langle Ty_n, y_n\rangle= & \lim \left[\|y\|^2 \big\langle T\frac{y}{\|y\|}, \frac{y}{\|y\|}\big\rangle + \|y_n-y\|^2\Big\langle T\frac{y_n-y}{\|y_n-y\|}, \frac{y_n-y}{\|y_n-y\|}\Big\rangle\right]\\
=& \|y\|^2 \big\langle T\frac{y}{\|y\|}, \frac{y}{\|y\|}\big\rangle + (1-\|y\|^2)\lim \Big\langle T\frac{y_n-y}{\|y_n-y\|}, \frac{y_n-y}{\|y_n-y\|}\Big\rangle .
\end{align*} We have just written ![]() $\overline\omega$ as a convex combination of
$\overline\omega$ as a convex combination of  $\omega=\langle T\frac{y}{\|y\|}, \frac{y}{\|y\|}\big\rangle \in W(T)$ and
$\omega=\langle T\frac{y}{\|y\|}, \frac{y}{\|y\|}\big\rangle \in W(T)$ and  $\omega_e= \lim \;\langle T\frac{y_n-y}{\|y_n-y\|}, \frac{y_n-y}{\|y_n-y\|}\Big\rangle$. We use Theorem 3.2 again, observing that
$\omega_e= \lim \;\langle T\frac{y_n-y}{\|y_n-y\|}, \frac{y_n-y}{\|y_n-y\|}\Big\rangle$. We use Theorem 3.2 again, observing that  $\left(\frac{y_n-y}{\|y_n-y\|}\right)_n$ is an essential sequence for we, to conclude that
$\left(\frac{y_n-y}{\|y_n-y\|}\right)_n$ is an essential sequence for we, to conclude that ![]() $w_e\in W_e(T)$. Therefore,
$w_e\in W_e(T)$. Therefore, ![]() $\overline\omega \in {{\rm iconv\,}}\{W_e(T), W(T)\}$.
$\overline\omega \in {{\rm iconv\,}}\{W_e(T), W(T)\}$.
As in other results concerning the quaternionic numerical range, next corollary shows that we can simply consider what happens in the complex plane. Given a quaternion ![]() $q=q_0+q_1i+q_2j+q_3k$, we define
$q=q_0+q_1i+q_2j+q_3k$, we define ![]() $\pi_{(1)}(q)={{\rm Re\,}}(q)=q_0$ and
$\pi_{(1)}(q)={{\rm Re\,}}(q)=q_0$ and ![]() $\pi_{(i)}(q)=q_1$.
$\pi_{(i)}(q)=q_1$.
Corollary 4.4. Let ![]() $T\in{\mathcal{B}}({\mathcal{H}})$. Then
$T\in{\mathcal{B}}({\mathcal{H}})$. Then ![]() $\overline{B(T)}={{\rm iconv\,}}\{B_e(T), B(T)\}$.
$\overline{B(T)}={{\rm iconv\,}}\{B_e(T), B(T)\}$.
Proof. From Theorem 4.3, we have
We obtain that ![]() ${{\rm iconv\,}}\{B_e(T), B(T)\} \subseteq \overline{B(T)}$.
${{\rm iconv\,}}\{B_e(T), B(T)\} \subseteq \overline{B(T)}$.
For the converse inclusion, take an element ![]() $\bar\omega \in \overline{B(T)}$. According to Theorem 4.3, there are
$\bar\omega \in \overline{B(T)}$. According to Theorem 4.3, there are ![]() $\omega \in W(T)$,
$\omega \in W(T)$, ![]() $\omega_e \in W_e(T)$ and
$\omega_e \in W_e(T)$ and ![]() $\alpha \in [0,1]$, such that
$\alpha \in [0,1]$, such that
Observe that when α = 0 or α = 1 the inclusion immediately follows. So suppose ![]() $\alpha\neq 0, 1$.
$\alpha\neq 0, 1$.
We can write ![]() $\omega=a+bq$ and
$\omega=a+bq$ and ![]() $w_e=c+dq_e$, where
$w_e=c+dq_e$, where ![]() $a, b, c, d\in {\mathbb{R}}$,
$a, b, c, d\in {\mathbb{R}}$, ![]() $q\in {{\rm Im\,}}(q)$,
$q\in {{\rm Im\,}}(q)$, ![]() $q_e\in {{\rm Im\,}}(q_e)$ and
$q_e\in {{\rm Im\,}}(q_e)$ and ![]() $|q|=|q_e|=1$. Therefore, we have
$|q|=|q_e|=1$. Therefore, we have
Note that ![]() $\alpha bq+(1-\alpha)dq_e\in {\text{span}\,}\{i\}$, since
$\alpha bq+(1-\alpha)dq_e\in {\text{span}\,}\{i\}$, since ![]() $\bar\omega\in {\mathbb{C}}$. Assume that
$\bar\omega\in {\mathbb{C}}$. Assume that ![]() $\bar\omega\in {\mathbb{C}}^+$. If
$\bar\omega\in {\mathbb{C}}^+$. If ![]() $\bar\omega\in {\mathbb{C}}^-$, the proof is analogous.
$\bar\omega\in {\mathbb{C}}^-$, the proof is analogous.
By the axial symmetry over the reals of the numerical range, there are ![]() $\omega_{(i)} \in [\omega] \cap {\mathbb{C}}^+$ in the bild and
$\omega_{(i)} \in [\omega] \cap {\mathbb{C}}^+$ in the bild and ![]() $\omega_{e,(i)} \in [\omega_e] \cap {\mathbb{C}}^+$. We can write
$\omega_{e,(i)} \in [\omega_e] \cap {\mathbb{C}}^+$. We can write ![]() $\omega_i=a+|b|i$ and
$\omega_i=a+|b|i$ and ![]() $\omega_{e,i}=c+|d|i$.
$\omega_{e,i}=c+|d|i$.
Define ![]() $\overline{\omega}_i=\alpha\omega_i+(1-\alpha)\omega_{e,i}$, which can be written as
$\overline{\omega}_i=\alpha\omega_i+(1-\alpha)\omega_{e,i}$, which can be written as
Clearly, ![]() $\pi_{(1)}(\bar\omega)=\pi_{(1)}(\bar\omega_i)$. On the other hand, since
$\pi_{(1)}(\bar\omega)=\pi_{(1)}(\bar\omega_i)$. On the other hand, since ![]() $\alpha bq+(1-\alpha)dq_e\in {\text{span}\,}\{i\}$ and
$\alpha bq+(1-\alpha)dq_e\in {\text{span}\,}\{i\}$ and ![]() $|q|=|q_e|=1$, we have
$|q|=|q_e|=1$, we have
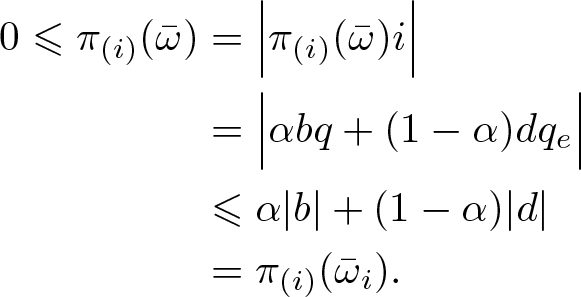 \begin{align*}
0 \leqslant \pi_{(i)}(\bar\omega) &= \Big|\pi_{(i)}(\bar\omega)i\Big|\\
&=\Big|\alpha bq+(1-\alpha)dq_e\Big|\\
&\leqslant\alpha \lvert b\rvert+(1-\alpha)\lvert d\rvert\\
&=\pi_{(i)}(\bar\omega_i).
\end{align*}
\begin{align*}
0 \leqslant \pi_{(i)}(\bar\omega) &= \Big|\pi_{(i)}(\bar\omega)i\Big|\\
&=\Big|\alpha bq+(1-\alpha)dq_e\Big|\\
&\leqslant\alpha \lvert b\rvert+(1-\alpha)\lvert d\rvert\\
&=\pi_{(i)}(\bar\omega_i).
\end{align*} Assuming that ![]() $\alpha |b|-(1-\alpha)|d|\geqslant 0$, let now
$\alpha |b|-(1-\alpha)|d|\geqslant 0$, let now ![]() $\widetilde{\omega}_i=\alpha\omega_i+(1-\alpha)\omega^*_{e,i}$; otherwise, define
$\widetilde{\omega}_i=\alpha\omega_i+(1-\alpha)\omega^*_{e,i}$; otherwise, define ![]() $\widetilde{\omega}_i=\alpha\omega_i^*+(1-\alpha)\omega_{e,i}$. Clearly,
$\widetilde{\omega}_i=\alpha\omega_i^*+(1-\alpha)\omega_{e,i}$. Clearly, ![]() $\widetilde{\omega}_i\in {\mathbb{C}}^+$ and
$\widetilde{\omega}_i\in {\mathbb{C}}^+$ and ![]() $\pi_{(1)}(\widetilde{\omega_i})=\pi_{(1)}(\overline{\omega})$. We have
$\pi_{(1)}(\widetilde{\omega_i})=\pi_{(1)}(\overline{\omega})$. We have
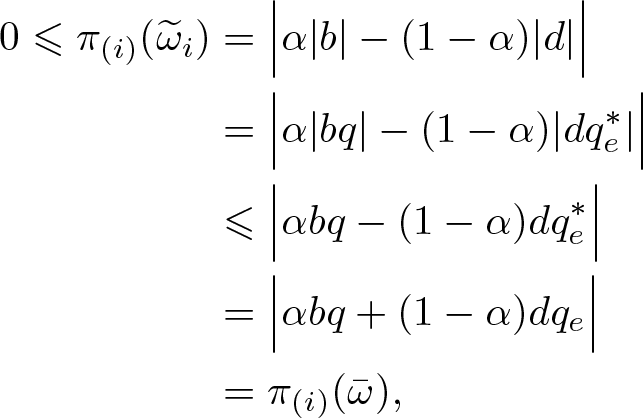 \begin{align*}
0 \leqslant \pi_{(i)}(\widetilde{\omega}_i) &= \Big|\alpha |b|-(1-\alpha)|d|\Big|\\
&=\Big|\alpha \lvert bq\rvert-(1-\alpha)\lvert dq_e^*\rvert\Big|\\
&\leqslant \Big|\alpha bq-(1-\alpha)dq_e^*\Big|\\
&= \Big|\alpha bq+(1-\alpha)dq_e\Big|\\
&= \pi_{(i)}(\bar\omega),
\end{align*}
\begin{align*}
0 \leqslant \pi_{(i)}(\widetilde{\omega}_i) &= \Big|\alpha |b|-(1-\alpha)|d|\Big|\\
&=\Big|\alpha \lvert bq\rvert-(1-\alpha)\lvert dq_e^*\rvert\Big|\\
&\leqslant \Big|\alpha bq-(1-\alpha)dq_e^*\Big|\\
&= \Big|\alpha bq+(1-\alpha)dq_e\Big|\\
&= \pi_{(i)}(\bar\omega),
\end{align*} since ![]() $\alpha bq+(1-\alpha)dq_e\in {\text{span}\,}\{i\}$ and
$\alpha bq+(1-\alpha)dq_e\in {\text{span}\,}\{i\}$ and ![]() $\overline{\omega}\in{\mathbb{C}}^+$.
$\overline{\omega}\in{\mathbb{C}}^+$.
Then we have found two elements ![]() $\bar \omega_{i}$ and
$\bar \omega_{i}$ and ![]() $\tilde \omega_{i}$, both in
$\tilde \omega_{i}$, both in ![]() ${{\rm iconv\,}}\{B_e(T), B(T)\}$, such that
${{\rm iconv\,}}\{B_e(T), B(T)\}$, such that
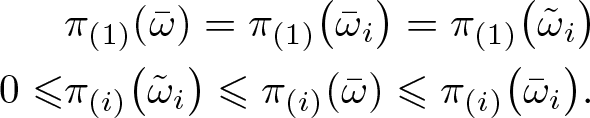 \begin{align*}
&\pi_{(1)}(\bar\omega)=\pi_{(1)} \big(\bar \omega_{i}\big)=\pi_{(1)}\big(\tilde \omega_{i}\big)\\
0\leqslant &\pi_{(i)}\big(\tilde \omega_{i} \big)\leqslant \pi_{(i)}(\bar \omega) \leqslant \pi_{(i)} \big(\bar \omega_{i} \big).
\end{align*}
\begin{align*}
&\pi_{(1)}(\bar\omega)=\pi_{(1)} \big(\bar \omega_{i}\big)=\pi_{(1)}\big(\tilde \omega_{i}\big)\\
0\leqslant &\pi_{(i)}\big(\tilde \omega_{i} \big)\leqslant \pi_{(i)}(\bar \omega) \leqslant \pi_{(i)} \big(\bar \omega_{i} \big).
\end{align*} Now we will show that ![]() $\overline{\omega}$ is also in
$\overline{\omega}$ is also in ![]() ${{\rm iconv\,}}\{B_e(T), B(T)\}$. Consider the affine transformation
${{\rm iconv\,}}\{B_e(T), B(T)\}$. Consider the affine transformation
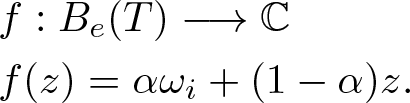 \begin{align*}
& f:B_e(T)\longrightarrow {\mathbb{C}}\\
&f(z)=\alpha \omega_i+(1-\alpha)z. \,
\end{align*}
\begin{align*}
& f:B_e(T)\longrightarrow {\mathbb{C}}\\
&f(z)=\alpha \omega_i+(1-\alpha)z. \,
\end{align*} Since ![]() $B_e(T)$ is convex,
$B_e(T)$ is convex, ![]() $[\omega^*_{e,i}, \omega_{e,i}]\subset B_e(T)$. Affine transformations map lines into lines so we have
$[\omega^*_{e,i}, \omega_{e,i}]\subset B_e(T)$. Affine transformations map lines into lines so we have
Observe that ![]() $\widetilde{\omega}_i\neq \overline{\omega}_i$, since α ≠ 1.
$\widetilde{\omega}_i\neq \overline{\omega}_i$, since α ≠ 1.
Since ![]() $\overline{\omega}\in [\widetilde{\omega}_i, \overline{\omega}_i]$, there exists
$\overline{\omega}\in [\widetilde{\omega}_i, \overline{\omega}_i]$, there exists ![]() $\eta\in [\omega^*_{e,i}, \omega_{e,i}]\subset B_e(T)$ such that
$\eta\in [\omega^*_{e,i}, \omega_{e,i}]\subset B_e(T)$ such that ![]() $f(\eta)=\overline{\omega},$ that is,
$f(\eta)=\overline{\omega},$ that is, ![]() $\alpha \omega_i+(1-\alpha)\eta=\overline{\omega}$. We conclude that
$\alpha \omega_i+(1-\alpha)\eta=\overline{\omega}$. We conclude that ![]() $\overline{\omega}\in {{\rm iconv\,}}\{B_e(T), B(T)\}$.
$\overline{\omega}\in {{\rm iconv\,}}\{B_e(T), B(T)\}$.
Remark 4.5. In the complex setting, [Reference Lancaster11, Corollary 1] proves that the numerical range is closed if and only if the ![]() $W_{{\mathbb{C}},e}(T)$ is a subset of the
$W_{{\mathbb{C}},e}(T)$ is a subset of the ![]() $W_{\mathbb{C}}(T)$. The relation in the previous result induces the idea that the same result might hold for quaternions. However, that is not the case.
$W_{\mathbb{C}}(T)$. The relation in the previous result induces the idea that the same result might hold for quaternions. However, that is not the case.
Take the operator ![]() $T={\text{diag}\,}\{-1+i, 1+i\}\oplus \text{diag}\{s_n\}$, where sn is a sequence that runs over
$T={\text{diag}\,}\{-1+i, 1+i\}\oplus \text{diag}\{s_n\}$, where sn is a sequence that runs over ![]() $(-1/2,1/2)i\cap \mathbb{Q}i$. Applying Theorem 3.2 and Theorem 4.2, we have
$(-1/2,1/2)i\cap \mathbb{Q}i$. Applying Theorem 3.2 and Theorem 4.2, we have
From Theorem 4.2 in [Reference Carvalho, Diogo and Mendes6], it follows
Nevertheless, the upper bild, and therefore the bild, is not closed. For example, the boundary line segment joining ![]() $-1/3$ to
$-1/3$ to ![]() $-1+i$ does not belong to B(T). Thus, we have
$-1+i$ does not belong to B(T). Thus, we have ![]() $B_e(T)=[-i/2,i/2]\subseteq B(T)$ but B(T) is not closed.
$B_e(T)=[-i/2,i/2]\subseteq B(T)$ but B(T) is not closed.
Competing interests
The authors declare none.



